顾名思义,扫描法就是用一根想象中的线扫过所有矩形,在写代码的过程中,这根线很重要。方向的话,可以左右扫,也可以上下扫。方法是一样的,这里我用的是由下向上的扫描法。
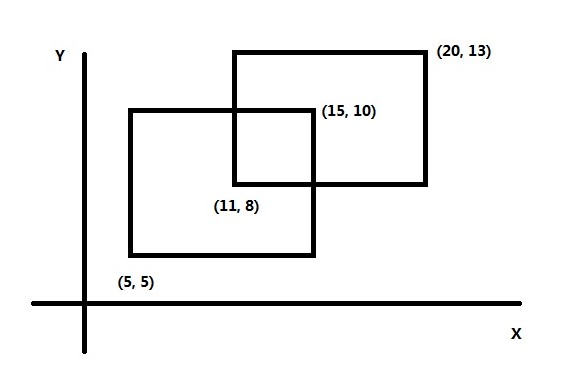
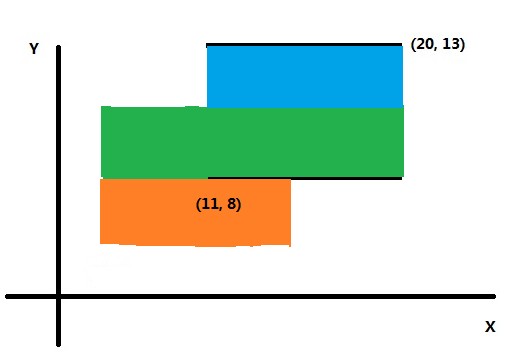
如上图所示,坐标系内有两个矩形。位置分别由左下角和右上角顶点的坐标来给出。上下扫描法是对x轴建立线段树,矩形与y平行的两条边是没有用的,在这里直接去掉。如下图。
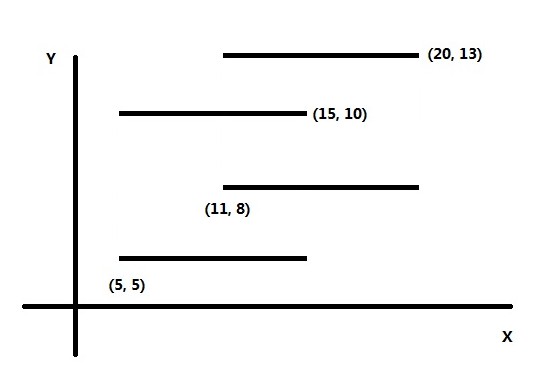
现想象有一条线从最下面的边开始依次向上扫描。线段树用来维护当前覆盖在x轴上的线段的总长度,初始时总长度为0。用ret来保存矩形面积总和,初始时为0。
由下往上扫描,扫描到矩形的底边时将它插入线段树,扫描到矩形的顶边时将底边从线段树中删除。而在代码中实现的方法就是,每条边都有一个flag变量,底边为1,顶边为-1。
用cover数组(通过线段树维护)来表示某x轴坐标区间内是否有边覆盖,初始时全部为0。插入或删除操作直接让cover[] += flag。当cover[] > 0 时,该区间一定有边覆盖。
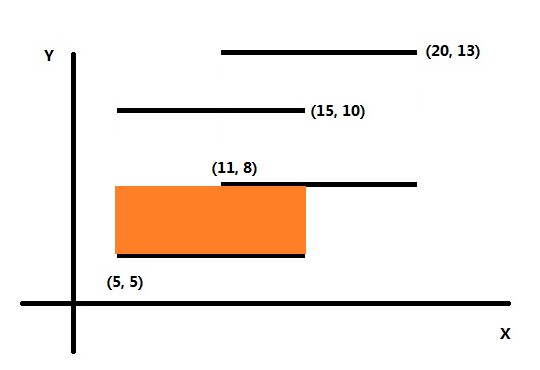
开始扫描到第一条线,将它压入线段树,此时覆盖在x轴上的线段的总长度L为10。计算一下它与下一条将被扫描到的边的距离S(即两条线段的纵坐标之差,该例子里此时为3)。
则 ret += L * S. (例子里增量为10*3=30)
结果如下图
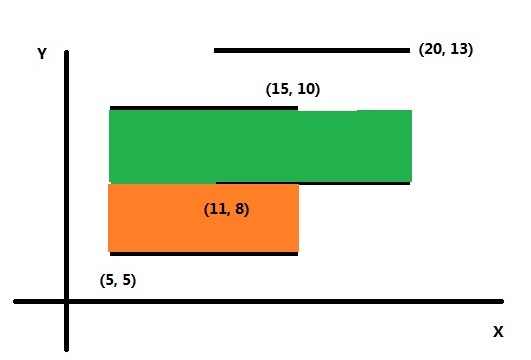
扫描到第二条边,将它压入线段树,计算出此时覆盖在x轴上的边的总长度。
例子里此时L=15。与下一条将被扫描到的边的距离S=2。 ret += 30。 如下图所示。
接下来扫描到了下方矩形的顶边,从线段树中删除该矩形的底边,并计算接下来面积的增量。如下图
此时矩形覆盖的总面积已经计算完成。 可以看到,当共有n条底边和顶边时,只需要从下往上扫描n-1条边即可计算出总面积。
定义节点和线段:
1 class TreeNode 2 { 3 public: 4 int left; 5 int right; 6 int mid; 7 int cover; 8 int flag; 9 double length; 10 }; 11 typedef struct 12 { 13 double xl, xr, y; 14 int flag; 15 }Line;
建树:
1 void BuildTree(int k, int l, int r) 2 { 3 node[k].left = l; 4 node[k].right = r; 5 node[k].mid = (l + r) >> 1; 6 node[k].cover = 0; 7 node[k].flag = 0; 8 if(l + 1 == r) 9 { 10 node[k].flag = 1; 11 return ; 12 } 13 int mid = (l + r) >> 1; 14 BuildTree(k << 1, l, mid); 15 BuildTree(k << 1|1, mid, r); 16 }
更新:
1 void UpdateTree(int k, int l, int r, int flag) 2 { 3 if(node[k].left == l && node[k].right == r) 4 { 5 node[k].cover += flag; 6 node[k].length = x[r-1] - x[l-1]; 7 return ; 8 } 9 if(node[k].flag) 10 return ; 11 if(node[k].mid <= l) 12 UpdateTree(k << 1|1, l, r, flag); 13 else if(node[k].mid >= r) 14 UpdateTree(k << 1, l, r, flag); 15 else 16 { 17 UpdateTree(k << 1, l, node[k].mid, flag); 18 UpdateTree(k << 1|1, node[k].mid, r, flag); 19 } 20 }
查询有效长度:
1 void GetLength(int k) 2 { 3 if(node[k].cover > 0) 4 { 5 length += node[k].length; 6 return ; 7 } 8 if(node[k].flag) 9 return; 10 GetLength(k << 1); 11 GetLength(k << 1|1); 12 }
找离散后的位置:
1 int GetIndex(double num, int length) 2 { 3 int l, r, mid; 4 l = 0, r = length; 5 while(l <= r) 6 { 7 mid = (l + r) >> 1; 8 if(x[mid] == num) 9 return mid; 10 else if(x[mid] > num) 11 r = mid - 1; 12 else 13 l = mid + 1; 14 } 15 }
排序,离散化:
1 for(i = 0; i < n; i ++) 2 { 3 scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2); 4 seg[j].xl = x1; 5 seg[j].xr = x2; 6 seg[j].y = y1; 7 x[j] = x1; 8 seg[j ++].flag = 1; 9 seg[j].xl = x1; 10 seg[j].xr = x2; 11 seg[j].y = y2; 12 x[j] = x2; 13 seg[j ++].flag = -1; 14 } 15 sort(x, x+j); 16 sort(seg, seg+j, cmp); 17 k = 1; 18 for(i = 1; i < j; i ++) 19 { 20 if(x[i] != x[i-1]) 21 x[k ++] = x[i]; 22 }