二叉树遍历操作的实现
一、实验内容
1.实验目的
二叉树是“树”结构里的一个重要概念,指每个结点最多有两个子树的树结构。所谓遍历是指沿着某条搜索路线,依次对二叉树中每个结点均做一次且仅做一次访问。鉴于二叉树是非线性结构的事实,若对二叉树 进行遍历,首先要选择链式存储结构来构建一棵二叉树,再运用特殊的遍历方法(先序、中序和后序)来实现操作。
本实验使用高级编程语言C语言,来实现按先序遍历的顺序构建一棵基于二叉链表存储结构的二叉树,并对构建的二叉树实现先序、中序和后序遍历,并输出对应的遍历序列。通过实验熟悉二叉树的遍历操作。
2.实验内容
1) 构建一个二叉链表存储结构的二叉树,通常应包含如下步骤:
a.定义用来描述二叉树结点的结构体变量类型BiTNode,成员包括data,lchild,rchild分别对应结点存储的数据、左孩子和右孩子;
b.编写一个二叉树构建算法,记为CreateBiTree操作(函数),利用二叉链表存储结构构建二叉树;
2)基于上述构建的二叉树进行先序、中序和后序遍历操作:
a.编写三个函数PreOrderTraverse、InOrderTraverse和PostOrderTraverse,分别用来进行先序、中序和后序操作。
b.编写visit方法,访问各个结点存储的数据及相关信息;
c.在main函数内部,初始化一个根结点,调用上述方法实现二叉树的构建与遍历;
d.编译运行程序,评估实验结果.
3)完成实验报告的填写
3.实验原理
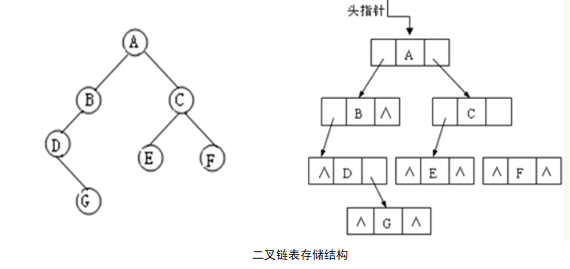
二叉链表:二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。其结点结构为:

其中,data域存放某结点的数据信息;lchild与rchild分别存放指向左孩子和右孩子的指针,当左孩子或右孩子不存在时,相应指针域值为空(用符号∧或NULL表示)。利用这样的结点结构表示的二叉树的链式存储结构被称为二叉链表。
二、实验过程
1.BiTNode结构体定义
首先用C/C++开发环境新建源文件,首先键入如下预定义命令行:
#include <stdio.h>
#include <stdlib.h>
针对在构建二叉树的实际操作中需要的malloc函数,首先需要在源代码的头部引用stdlib.h文件。
接着,根据二叉链表的逻辑结构原理图,定义用来描述的结构体变量类型BiTNode和结构体指针类型BiTree,假设本实验构建的二叉树存储char型数据元素,代码如下:
typedef char ElemType; typedef struct BiTNode{ ElemType data; struct BiTNode *lchild,*rchild; }BiTNode, *BiTree;
这里用lchild和rchild分别指向当前结点的左子树(根结点)和右子树(根结点)。
2.CreateBiTree函数
编写CreateBiTree函数按照先序遍历的方式来创建一棵二叉树,参数列表接收一个双重指针T,用来实现二叉树创建过程中的递归操作。
在函数内部,首先指定用户输入需要存入二叉树的char型数据,并规定用户’_’下划线输入表示当前结点(子树)不存在,反之为当前结点分配内存空间,并将用户输入的数据存入二叉链表结点的数据域,然后利用递归机制为当前结点创建左子树和右子树,直到输入二叉树的所有叶子结点数据,递归停止。
代码如下:
// 创建一颗二叉树,按照先序遍历的方式输入数据 void CreateBiTree(BiTree *T){ ElemType c; scanf("%c",&c); if('_'==c){ *T = NULL; }else{ *T = (BiTNode *)malloc(sizeof(BiTNode)); (*T)->data = c; CreateBiTree(&(*T)->lchild); CreateBiTree(&(*T)->rchild); } }
3. visit函数
编写visit函数实现用户访问二叉树结点的具体操作,参数列表用来接收当前二叉树结点存储的数据值和所在层数(char型,int型)。
在函数内部,直接使用printf()函数将参数列表接收的数据输出。
// 访问二叉树结点的具体操作 void visit(char c, int level){ printf("%c位于第%d层 ",c,level); }
4. 遍历二叉树方法
编写PreOrderTraverse函数实现先序遍历二叉树,参数列表用来接收当前二叉树的结点指针T和所在层数level(BiTree型,int型)。
在函数内部,首先,用条件语句判断二叉树是否为空,若为空,函数将不进行任何操作;若非空,则首先调用visit函数访问根结点,接着递归调用函数本身,来遍历左子树,最后遍历右子树,同时为传入参数列表的实参level增1,表示遍历当前子树的根结点所在层数发生改变,层数增加。直到遍历完叶子结点后,递归调用结束。
PreOrderTraverse函数运用递归的思想可以实现先序遍历二叉树,在无需知道二叉树深度的情况下可以准确无误地遍历整棵二叉树,这是递归思想的具体体现。
代码如下:
// 先序遍历二叉树 void PreOrderTraverse(BiTree T, int level){ if(T){ visit(T->data, level); PreOrderTraverse(T->lchild, level+1); PreOrderTraverse(T->rchild, level+1); } }
编写InOrderTraverse函数实现中序遍历二叉树,参数列表用来接收当前二叉树的结点指针T和所在层数level(BiTree型,int型)。
在函数内部,首先,用条件语句判断二叉树是否为空,若为空,函数将不进行任何操作;若非空,则首先递归调用函数本身,遍历左子树,接着调用visit函数访问根结点,最后遍历右子树,同时为传入参数列表的实参level增1,表示遍历当前子树的根结点所在层数发生改变,层数增加。和PreOrderTraverse函数一样运用递归的思想可以实现中序遍历二叉树。
代码如下:
// 中序遍历二叉树 void InOrderTraverse(BiTree T, int level){ if(T){ InOrderTraverse(T->lchild, level+1); visit(T->data, level); InOrderTraverse(T->rchild, level+1); } }
编写PostOrderTraverse函数实现后序遍历二叉树,参数列表用来接收当前二叉树的结点指针T和所在层数level(BiTree型,int型)。
在函数内部,首先,用条件语句判断二叉树是否为空,若为空,函数将不进行任何操作;若非空,则首先递归调用函数本身遍历左子树,接着递归调用函数本身遍历右子树,最后调用visit函数访问根结点,同时为传入参数列表的实参level增1,表示遍历当前子树的根结点所在层数发生改变,层数增加。和PreOrderTraverse函数一样运用递归的思想可以实现后序遍历二叉树。
代码如下:
// 后序遍历二叉树 void PostOrderTraverse(BiTree T, int level){ if(T){ PostOrderTraverse(T->lchild, level+1); PostOrderTraverse(T->rchild, level+1); visit(T->data, level); } }
5. main函数的实现
int main(){ int level = 1; BiTree T = NULL; CreateBiTree(&T); printf("先序遍历 "); PreOrderTraverse(T,level); printf("中序遍历 "); InOrderTraverse(T,level); printf("后序遍历 "); PostOrderTraverse(T,level); return 0; }
1. 声明一个int型变量level用来初始化非空二叉树根结点所在层数;
2. 初始化一个BiTree型指针T,指定为NULL;
3. 调用CreateBiTree函数,传入T的地址,来创建一棵二叉树;
4. 调用PreOrderTraverse函数先序遍历二叉树;
5. 调用InOrderTraverse函数中序遍历二叉树;
6. 调用PostOrderTraverse函数后序遍历二叉树;
7. 编译运行,测试代码.
三、实验结果
(1)用户输入
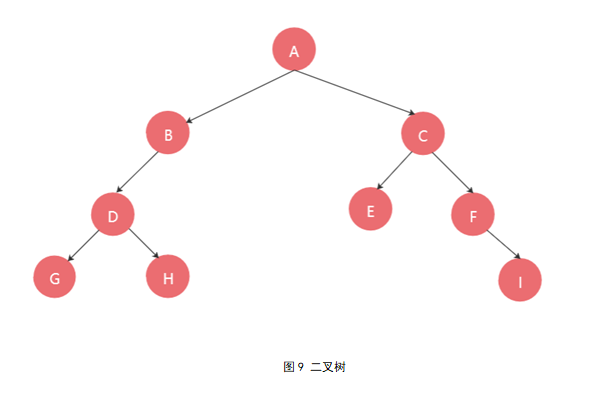
如图9所示,将这棵二叉树作为用户输入的实例来测试上述代码的实验结果是否正确可靠。由于用户主要以字符输入的方式向计算机描述自己构建的二叉树,所以首先要将二叉树转化为字符序列ABDG__H___CE__F_I__输入。
(2)预期输出
先序:ABDGHCEFI;中序:GDHBAECFI;后序:GHDBEIFCA.
(3)结果输出

实验结果与预期目标一致,能够实现利用二叉链表按照先序的方式来构建一棵二叉树,并基于该二叉树用先序、中序和后序三种方式遍历二叉树。
四、实验总结
通过“二叉树遍历操作的实现”这个实验,利用二叉链表存储结构来构建一棵二叉树并基于该二叉树通过先序、中序和后序三种方法实现遍历操作。
在实验的过程中,体会到了采用二叉链表构建二叉树的优点,就本实验而言,二叉树是一种非线性结构,从存储空间的意义来看,采用顺序存储结构浪费了一定的存储资源。而通过二叉链表,会大大减少不必要的空间开销。
对二叉树的遍历操作是递归思想的体现,递归调用无需考虑二叉树的深度,代码片段简洁,比循环遍历要简洁的多。但是递归调用在时间和空间上会产生一定的消耗。先序遍历DLR体现在代码中就是先访问根结点再遍历左子树和右子树;中序遍历LDR体现在代码中就是先遍历左子树,接着访问根结点,最后遍历右子树;后序遍历LRD体现在代码中就是先遍历左子树,接着遍历右子树,最后访问根结点。
二叉树的遍历应用到现实生活中可用来搜索磁盘中存储的文件或文件夹。
五、完整代码
#include <stdio.h> #include <stdlib.h> typedef char ElemType; typedef struct BiTNode{ ElemType data; struct BiTNode *lchild,*rchild; }BiTNode, *BiTree; // 创建一颗二叉树,按照先序遍历的方式输入数据 void CreateBiTree(BiTree *T){ ElemType c; scanf("%c",&c); if('_'==c){ *T = NULL; }else{ *T = (BiTNode *)malloc(sizeof(BiTNode)); (*T)->data = c; CreateBiTree(&(*T)->lchild); CreateBiTree(&(*T)->rchild); } } // 访问二叉树结点的具体操作 void visit(char c, int level){ printf("%c位于第%d层 ",c,level); } // 先序遍历二叉树 void PreOrderTraverse(BiTree T, int level){ if(T){ visit(T->data, level); PreOrderTraverse(T->lchild, level+1); PreOrderTraverse(T->rchild, level+1); } } // 中序遍历二叉树 void InOrderTraverse(BiTree T, int level){ if(T){ InOrderTraverse(T->lchild, level+1); visit(T->data, level); InOrderTraverse(T->rchild, level+1); } } // 后序遍历二叉树 void PostOrderTraverse(BiTree T, int level){ if(T){ PostOrderTraverse(T->lchild, level+1); PostOrderTraverse(T->rchild, level+1); visit(T->data, level); } } int main(){ int level = 1; BiTree T = NULL; CreateBiTree(&T); printf("先序遍历 "); PreOrderTraverse(T,level); printf("中序遍历 "); InOrderTraverse(T,level); printf("后序遍历 "); PostOrderTraverse(T,level); return 0; }