ACM学习历程—ZOJ3785 What day is that day?(数论)

Description

It's Saturday today, what day is it after 1¹ + 2² + 3³ + ... + N^N days?

Input

There are multiple test cases. The first line of input contains an integer T indicating the number of test cases. For each test case:

There is only one line containing one integer N (1 <= N <= 1000000000).

Output

For each test case, output one string indicating the day of week.

Sample Input

2
1
2

Sample Output

Sunday
Thursday

Hint

A week consists of Sunday, Monday, Tuesday, Wednesday, Thursday, Friday and Saturday.

题目相当于要求模7的余数

根据同余关系，相当于求如下的式子：

于是只需要根据n/7和n%7来计算了，因为每一列都是等比数列，公比是 

假设k为每一列的个数

对于i =1来说：

对于i =2来说：

对于i =3来说：

对于i =4来说：

对于i =5来说：

对于i =6来说：

对于i =7来说：

然后计算每一列的k就可以计算了。这里用了一下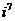的周期方便的运算，或者也可以直接无脑快速幂。

还有就是在前面过程中计算同余和逆元的时候，可以巧妙的把3变成-4，把5变成-2，把6变成-1，可以加快手算的速度。

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <algorithm>
#define LL long long

using namespace std;

int n;
char ans[][10] = {"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"};

int pow(int x, int y)
{
    int a = 1;
    for (int i = 0; i < y; ++i)
        a = (a*x)%7;
    return a;
}

int cal(int x, int p)
{
    if (x == 1)
        return p%7;
    if (x == 2)
        return (4*(pow(2, p%3)-1))%7;
    if (x == 3)
        return (3*(pow(3, p%6)-1))%7;
    if (x == 4)
        return (6*(pow(4, p%3)-1))%7;
    if (x == 5)
        return (6*(pow(5, p%6)-1))%7;
    if (x == 6)
        return (3*(pow(6, p%2)-1))%7;
    return 0;
}

void work()
{
    int s = 6, v, u;
    v = n/7;
    u = n%7;
    for (int i = 1; i <= u; ++i)
        s = (s+cal(i, v+1))%7;
    for (int i = u+1; i <= 7; ++i)
        s = (s+cal(i, v))%7;
    printf("%s
", ans[s]);
}

int main()
{
    //freopen("test.in", "r", stdin);
    int T;
    scanf("%d", &T);
    for (int times = 0; times < T; ++times)
    {
        scanf("%d", &n);
        work();
    }
    return 0;
}