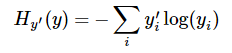softmax函数:

交叉熵:
其中指代实际的标签中第i个的值(用mnist数据举例,如果是3,那么标签是[0,0,0,1,0,0,0,0,0,0],除了第4个值为1,其他全为0)
就是softmax的输出向量[Y1,Y2,Y3...]中,第i个元素的值
显而易见,预测越准确,结果的值越小(别忘了前面还有负号),最后求一个平均,得到我们想要的loss。
过程如下:
第一步是先对网络最后一层的输出做一个softmax,这一步通常是求取输出属于某一类的概率,对于单样本而言,输出就是一个num_classes大小的向量([Y1,Y2,Y3...]其中Y1,Y2,Y3...分别代表了是属于该类的概率).
第二步是softmax的输出向量[Y1,Y2,Y3...]和样本的实际标签做一个交叉熵.
原始值[1, 2, 3]
softmax后[ 0.09003057 0.24472848 0.66524094]
和标签[0, 0, 1]做交叉熵,实际就是-1 * log(0.66524094)
代码示例:
在计算loss的时候,最常见的一句话就是tf.nn.softmax_cross_entropy_with_logits,那么它到底是怎么做的呢?
首先明确一点,loss是代价值,也就是我们要最小化的值
tf.nn.softmax_cross_entropy_with_logits(logits, labels, name=None)
除去name参数用以指定该操作的name,与方法有关的一共两个参数:
第一个参数logits:就是神经网络最后一层的输出,如果有batch的话,它的大小就是[batchsize,num_classes],单样本的话,大小就是num_classes
第二个参数labels:实际的标签,大小同上。
注意,这个函数的返回值并不是一个数,而是一个向量。如果要求交叉熵,我们要再做一步tf.reduce_sum操作,就是对向量里面所有元素求和,最后才得到;如果求loss,则要做一步tf.reduce_mean操作,对向量求均值!
# -*-coding: utf-8-*-
import tensorflow as tf
# our NN's output
logits = tf.constant([
[1.0, 2.0, 3.0],
[1.0, 2.0, 3.0],
[1.0, 2.0, 3.0]])
# steps1 do softmax
y = tf.nn.softmax(logits)
# ture label
y_ = tf.constant([[0.0, 0.0, 1.0],
[0.0, 0.0, 1.0],
[0.0, 0.0, 1.0]])
# step2: do cross_entopy
cross_entropy = -tf.reduce_sum(y_ * tf.log(y))
# do cross_entropy just one step
cross_entropy2 = tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=y_)) # dont forget tf.reduce_sum()!!
with tf.Session() as sess:
softmax = sess.run(y)
c_e = sess.run(cross_entropy)
c_e2 = sess.run(cross_entropy2)
print("step1:softmax result=")
print(softmax)
print("step2:cross_entropy result=")
print(c_e)
print("Function(softmax_cross_entropy_with_logits) result=")
print(c_e2)
输出:
step1:softmax result=
[[ 0.09003057 0.24472848 0.66524094]
[ 0.09003057 0.24472848 0.66524094]
[ 0.09003057 0.24472848 0.66524094]]
step2:cross_entropy result=
1.22282
Function(softmax_cross_entropy_with_logits) result=
1.22282
自己计算:
soft_max:e^1/(e^1+e^2+e^3)=0.09003057
cross_entropy: -1 * log(0.66524094) * 3= 1.2228
---------------------
作者:大师鲁
来源:CSDN
原文:https://blog.csdn.net/laolu1573/article/details/60138455
版权声明:本文为博主原创文章,转载请附上博文链接!