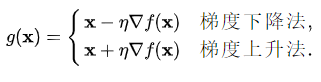一元函数的导数与Taylor级数
在微积分中，函数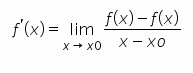
，它在几何上指的就是函数f(x)在x0上的切线方向。
通常来说，为了计算某个函数f(x)的最大值或者最小值，通常都计算他的导数f'(x)，然后求解方程f'(x)=0就可以得到函数的临界点，进一步判断这些临界点是否是最大值或者最小值。
但是，临界点并不一定是全局最大值或者是全局最小值，甚至不是局部的最大值或者局部最小值。
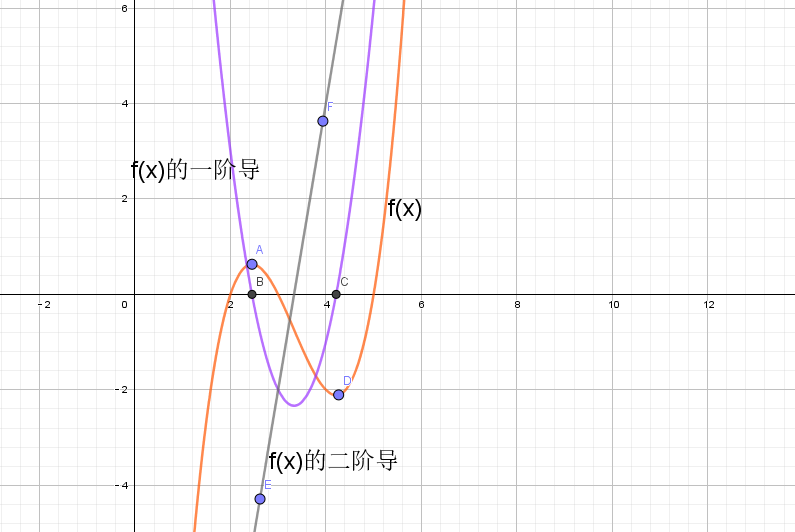
从泰勒级数的角度来看，
对于临界点x0而言，它满足条件f'(x0)=0。当f''(x0)>0时，可以得到x0是f(x)的局部最小值；当f''(x0)<0时，可以得到x0是f(x）的局部最大值。
多元函数的梯度和Taylor级数
对于多元函数f(x)=f(x1,x2,...,xn)而言，同样可以计算它们的导数，也就是偏导数和梯度，例如，梯度定义为
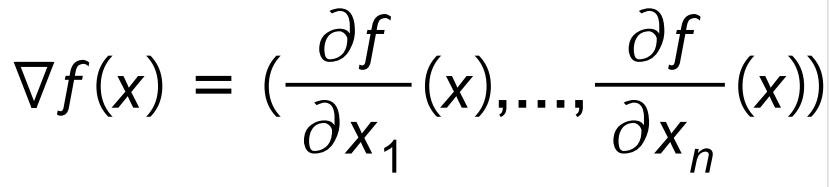
而多元函数f(x)在点x0上的泰勒级数是
其中H表示Hessian矩阵。如果x0是临界点，并且Hessian矩阵是正定矩阵的时候，f(x)在x0出达到局部极小值。
梯度下降法
从数学的角度来看，梯度的方向是函数增长速度最快的方向，那么梯度的反方向就是函数减少最快的方向。那么，如果想要计算一个函数的最小值，就可以使用梯度下降法的思想来做。假设希望求解目标函数
的最小值，可以从一个初始点
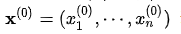开始，基于学习率
构建一个迭代过程；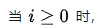
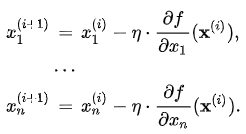
其中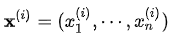
，一旦达到收敛条件的话，迭代就此结束。从梯度下降法的迭代公式来看，下一个点的选择与当前点的位置和它的梯度相关。反之，如果要计算函数
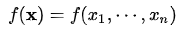的最大值，沿着梯度的反方向前进即可。即：
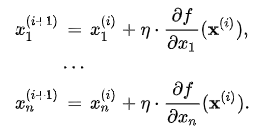
其中
，整体来看，无论是计算函数的最大值或者函数的最小值，都需要构建一个迭代关系g,即
也就是说对于所有的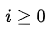
,都满足迭代关系
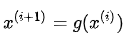。所以，写出函数g的表达式为
