整整三年没更新博客了,今天和女友聊天,聊到了博客,就回来看看。
最近接触到抽奖软件,下载的源码是http://download.csdn.net/detail/ghz_sd/6918125,在这里为开源软件作出贡献的人致敬,这个软件的作者a米山,是个非常好的人,耐心的帮我调试,他的算法很简单,就是纯粹的random,用的rand()函数,我给他提了个需求,写一个作弊类,实现的功能是:指定人的中奖概率提高,配置文件类似于这样:
<xml> <win> <name='a' probability=20> <name='b' probability=20> </win> </xml>
他实现的话,中奖了就给他好吃哈!!!
抽奖实际上用的是随机算法,在此进行归纳总结
一、选摘《算法导论》
在雇佣问题中,如果应聘者是以随机顺序出现的话,雇佣一个新的办公室助理的期望次数是lnn。这个算法是随着输入的变化而变化的。对于某个特定的输入,它总是会
产生固定的雇佣次数。
如果先对应聘者进行随机排列,此时随机发生在算法上而不是发生在输入分布上。 每次运行这个算法,执行依赖于随机的选择,而不是依赖于输入。这就是随机算法和概率分析的区别。
RANDOMIZED-HIRE-ASSISTANT(n)
1 randomly permute the list of candidates
2 best ← 0 ® candidate 0 is a least-qualified dummy candidate
3 for i ← 1 to n
4 do interview candidate i
5 if candidate i is better than candidate best
6 then best ← i
7 hire candidate i
随机算法事实上就是在算法里,对输入预先进行重排,其他完全一样。
在这里,要介绍2种对输入进行重排的算法,他们是随机重排。这两个方法都能产生均匀的随机排列。(每一种排列都等可能的被产生)。
要特别注意均匀随机排列的定义!!!!本书下面给出的2个算法对数组进行重排,产生的都是均匀随机排列,并给出了严格的数学证明,理论性很高,我们在这里这着重于介绍和了解这两种方法,不深究证明,欲看证明的可去看书。
---------------------------------------------------------------------------------------------------------------------------------------------------
随机排列数组:
1)PERMUTE-BY-SORTING(A)
为数组的每个元素赋一个随机的优先级,然后根据优先级对数组A进行排序。
PERMUTE-BY-SORTING(A)
1 n ← length[A]
2 for i ← 1 to n
3 do P[i] = RANDOM(1, n
3
) 4 sort A, using P as sort keys 5 return A
这样显然可以打乱数组的顺序,关键在于我们要去证明它是均匀随机打乱的。这个要根据均匀随机排列的定义,即证明产生每一个排列的概率都是1/n!
潜在的,我们可以知道:
a)如果一个算法总共还产生不到n!种排列,那么显然它不是一个均匀随机排列的算法。课后某习题
b)有人可能会说,要证明一个排列是均匀随机排列,只要证明每个元素在每个位置上出现的概率是1/n就可。这是对均匀随机排列的误解。课后某习题
PERMUTE-BY-SORTING比较难,不能直接看出可以产生多少种排列。
2)RANDOMIZE-IN-PLACE(A)
对数组一遍循环,每个元素A[i]与 A[i]到最后一个元素 中的某个交换(如下代码),容易看出,总共的排列数就是n!个
RANDOMIZE-IN-PLACE(A)
1 n ← length[A]
2 for i ← to n
3 do swap A[i] ↔ A[RANDOM(i, n)]
对于1)2)是均匀随机排列的证明这里就不讲了,书上有。
--------------------------------------------------------------------------------------------------------------------------------------------------
习题
(证明均匀随机排列的过程是非常麻烦的,我们重点关注上面画底线的a,b两条,来判断某个算法是否可以产生均匀随机排列就行)
5.3.2 Kelp教授决定用下列算法来随机产生非同一排列的任意排列,他实现了意图吗?
PERMUTE-WITHOUT-IDENTITY(A)
1 n ← length[A]
2 for i ← 1 to n
3 do swap A[i] ↔ A[RANDOM(i + 1, n)]
不行,这段代码总共只能产生(n-1)!种排列(自己算),达到他的意图的必要条件就需要能够产生n!-1种排列。
上述第a)点。
5.3.3 假设不是将 A[i] 与 A[i....n] 上的数随机的交换一个(注意这是我们的正确算法),而是每次将它与数组上任意位置上的数随机交换,可以产生均匀随机排列吗?
PERMUTE-WITH-ALL(A)
1 n ← length[A]
2 for i ← 1 to n
3 do swap A[i] ↔ A[RANDOM(1, n)]
不能,也是第a)点,可以自己分析下。
举个特例,假设排列长度为n=3。那么就要调用3次RANDOM,每次返回3个值中的一个,则执行完过程PERMUTE-WITH-ALL后将会有27种可能的结
果。因为排列长度为n,则一共有3!=6个排列,如果PERMUTE-WITH-ALL产生均匀的随机排列,那么每个排列出现的概率均为1/6。也就是说
每个排列都应该出现m次使m/27=1/6。由于不存在整数m使m/27=1/6,因此PERMUTE-WITH-ALL不一定产生均匀的随机排列。
5.3.4 Armstrong建议用下列过程来产生均匀随机排列:
PERMUTE-BY-CYCLIC(A) 1 n ← length[A] 2 offset ← RANDOM(1, n) 3 for i ← 1 to n 4 do dest ← i + offset 5 if dest > n 6 then dest ← dest -n 7 B[dest] ← A[i] 8 return B
证明任意元素在B中任意位置出现的概率都是1/n,证明该算法不能产生均匀随机排列。
1)注意第2行,offset在这就求出来了,在for中使用的时候是一个定值。
offset可以有n个值,所以任意元素在B中任意位置出现概率都是1/n.
2)这段代码只能产生n个不同的排列(原因仍是第2行)
这就说明了划线部分b)
二、抽奖概率-三种算法
点击标题即可跳转原博文
三、微信平台抽奖算法总结-再也不用怕奖品被提前抢光 http://www.xuanfengge.com/luck-draw.html(前端的网站都有算法文章)
前言
但凡商户搞点营销活动,为了能触达更多的顾客,来点儿抽奖的把戏,应该是极好的,什么“刮刮乐”、“砸金蛋”、“大转盘”等等,换汤不换药,屡试不爽。从微客多营销平台各种活动的使用情况也能看出,抽奖活动一直是商户用得最多的线上活动,正所谓无利不起早,给点“花蜜”犒劳下“蜜蜂”也是应该的。
需求分析
那么问题来了,发奖机制怎么玩?作为一个服务商户的营销平台,怎样将商户配置的奖品发出去才能起到比较好的效果呢?
先来看目标,什么是比较好的效果,也就是用户(商户)的需求是什么:
- 抽奖活动期间奖品数量是固定的
- 稀有的奖品尽量靠后被抽中
- 物尽其用,奖品不希望有剩余
- 每个奖品可以设置被抽中的概率
场景模拟
为了讨论方便,我们先把场景假设一下:
抽奖活动时间:
00:00:00-23:59:59
奖品设置:
| 奖品级别 | 奖品名称 | 奖品数量 |
| 一等奖 | A | 2 |
| 二等奖 | B | 3 |
| 三等奖 | C | 4 |
具体分析
第一种能想到的做法就是给每种奖品设置中奖概率,每次按设置好的中奖概率派奖,但是问题又来了:
奖品数量固定,但是参与抽奖的人数不可预知,根本无法控制奖品的消耗速度,如果概率设置高了,抽奖者一拥而上奖品很快就没了,设置低了,奖品可能到最后都发不完。另外,概率这个偏技术的术语用户理解起来肯定五花八门,使用时沟通成本非常高。
而实际上“每个奖品可以设置被抽中的概率”是个十分模糊的说法,说它模糊,主要是因为你并不知道这个设置的概率用在什么地方,这些概率设置需要满足什么条件,总样本数量(总抽奖次数)是多少。
所以最好的做法应该是用户不必关心所谓的“奖品被抽中的概率”,只关注前三个预期效果即可。
经过分析,我们发现,要达到用户上面的那三个效果,只要奖品在活动期间陆续被抽走即可,那能不能给每件奖品设置一个允许被抽走的时间呢?对!如果控制好每件奖品的发放时间点,再安排好各类奖品的发放顺序,大奖不会一开始就抽走,直到活动最后阶段都能保证有奖。
具体设计
顺着这个想法,我们来看具体的设计:
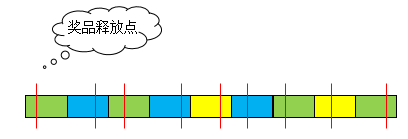
将奖品均匀地埋在整个活动时间(3600*24=86400秒)里,如上面假设场景,一共有9个奖品,则把活动时间均匀的分成9份
以奖品剩余数量作为权重,陆续随机选择每个时间段里的奖品类型(颜色对应的奖品见上表)
在每个时间段里随机选择奖品的“释放”时间点,一是为了均匀,二是避免直接暴露精确的时间点
|
1
|
releaseTime(n)=startTime+(n-1)× ∆t+random(∆t)
|
实现方案
说完思路,我们再看实现:在奖品释放时间点之后的抽奖用户就有机会(这个概率可配置,如100%或者80%)拿到该时间段的奖品,如果奖品未被抽走,将继续等待抽奖者的到来。
思路一
直观的做法是建立三张表
t_award_batch(奖品描述表,用于记录各种奖品的配置信息),
| ID | 名称(name) | 奖品总量(amount) |
| 1 | A | 2 |
| 2 | B | 3 |
| 3 | C | 4 |
t_award_pool(奖池表,用于生成每一次奖品释放的时间点),
| ID | 奖品ID(award_id) | 释放时间(release_time) | 剩余数(balance) |
| 1 | 3 | 1:03:27 | 0 |
| 2 | 2 | 3:15:13 | 1 |
| 3 | 3 | 5:29:57 | 1 |
| 4 | 2 | 9:35:34 | 1 |
| 5 | 1 | 12:57:20 | 1 |
| 6 | 2 | 13:47:03 | 1 |
| 7 | 3 | 17:31:50 | 1 |
| 8 | 1 | 18:13:26 | 1 |
| 9 | 3 | 22:28:40 | 1 |
t_record(抽奖记录表,用于记录每次抽奖者的抽奖记录)
| ID | 奖品ID(award_id) | 中奖时间(hit_time) | 用户ID(owner_id) |
| 1 | 3 | 1:03:45 | peteryan |
活动开始前,根据t_award_batch中的奖品配置信息,初始化t_award_pool中的数据,把每种奖品的释放时间初始化好,用户来抽奖时,根据当前时间在t_award_pool表中的查询到一条已经释放而且未被抽掉的奖品
|
1
|
select id from t_award_pool where release_time <= now() and balance > 0 limit 1 ;
|
查询到后对其进行更新,如果被他人抢走,则未中奖
|
1
|
update t_award_pool set balance = balance – 1 where id = #{id} balance > 0 ;
|
同时留下抽奖情况到t_record中。
思路二
在思路一中,为了方便抽奖时判断当前是否有可中奖品,进行了初始化每件奖品的释放时间,当奖品数量比较小的时候,情况还好,对于奖品数非常多的时候,抽奖的查询耗时会增加,初始化奖池也是耗时的动作,是否可以不依赖这个表之间通过实时计算判断当前是否有奖品释放。
在t_award_batch表中添加两个字段,奖品总剩余量balance和上一次中奖时间last_update_time。
| ID | 名称(name) | 奖品总量(amount) | 奖品余量(balance) | 更新时间(last_update_time) |
| 1 | A | 2 | 2 | 1:03:45 |
| 2 | B | 3 | 3 | 0:00:00 |
| 3 | C | 4 | 3 | 0:00:00 |
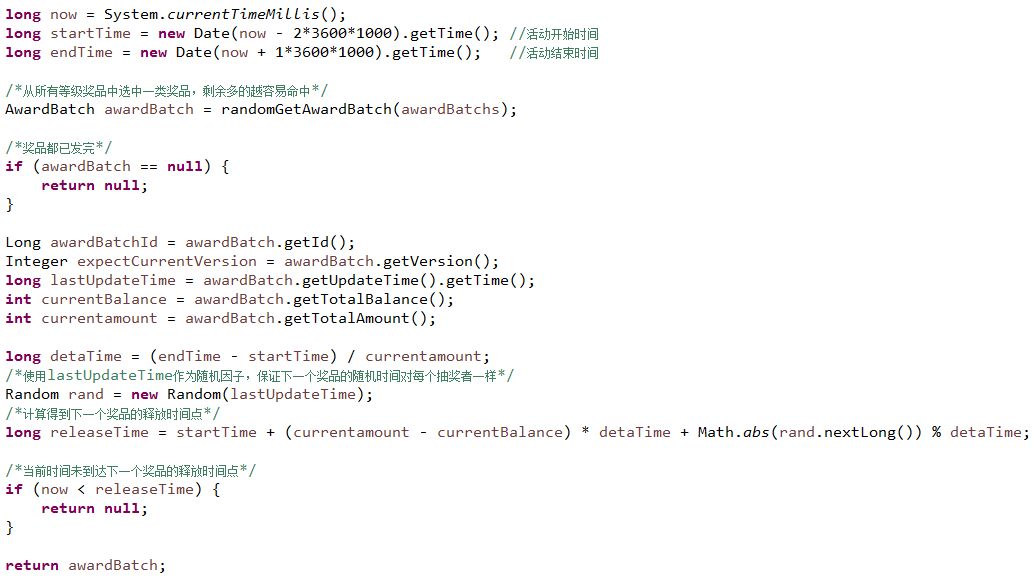
这样具体实现上仅需要依赖奖品配置信息即可,示例代码如下(点击图片全屏查看):
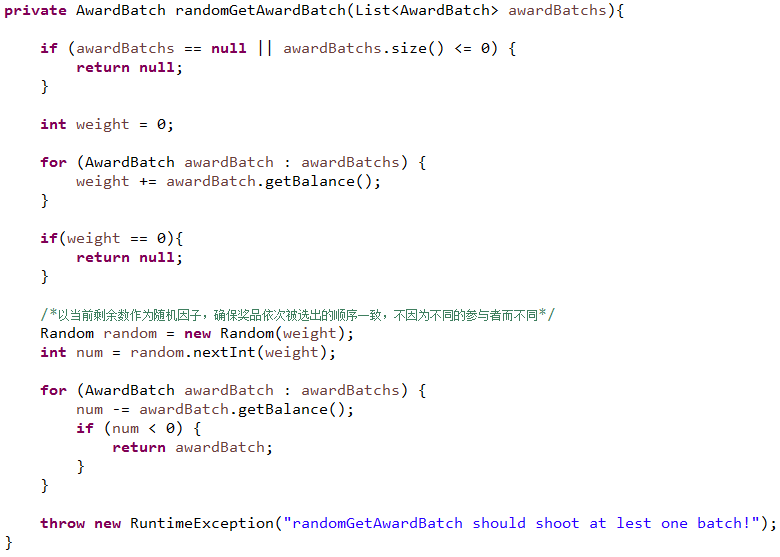
其中awardBatch表示一类奖品,如上表中提到的一等奖。上面代码中,随机选出下一个待释放的奖品逻辑如下:
通过这套发奖机制,很好地满足了营销商户的目标,同时减少了对复杂概率计算的纠结,再也不用担心奖品被提前抢光了。