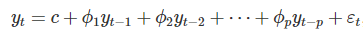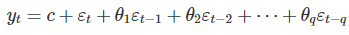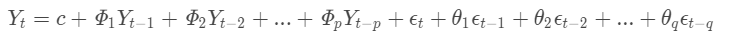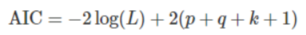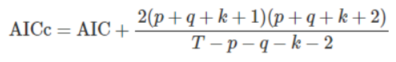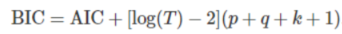用python做时间序列预测九：ARIMA模型简介

本篇介绍时间序列预测常用的ARIMA模型，通过了解本篇内容，将可以使用ARIMA预测一个时间序列。

什么是ARIMA？

• ARIMA是'Auto Regressive Integrated Moving Average'的简称。
• ARIMA是一种基于时间序列历史值和历史值上的预测误差来对当前做预测的模型。
• ARIMA整合了自回归项AR和滑动平均项MA。
• ARIMA可以建模任何存在一定规律的非季节性时间序列。
• 如果时间序列具有季节性，则需要使用SARIMA(Seasonal ARIMA)建模，后续会介绍。

ARIMA模型参数

ARIMA模型有三个超参数：p,d,q

• p
  AR(自回归)项的阶数。需要事先设定好，表示y的当前值和前p个历史值有关。

• d
  使序列平稳的最小差分阶数，一般是1阶。非平稳序列可以通过差分来得到平稳序列，但是过度的差分，会导致时间序列失去自相关性，从而失去使用AR项的条件。

• q
  MA(滑动平均)项的阶数。需要事先设定好，表示y的当前值和前q个历史值AR预测误差有关。实际是用历史值上的AR项预测误差来建立一个类似归回的模型。

ARIMA模型表示

• AR项表示
  一个p阶的自回归模型可以表示如下：
  
  c是常数项，εt是随机误差项。
  对于一个AR(1)模型而言：
  当 ϕ1=0 时,yt 相当于白噪声；
  当 ϕ1=1 并且 c=0 时,yt 相当于随机游走模型；
  当 ϕ1=1 并且 c≠0 时,yt 相当于带漂移的随机游走模型；
  当 ϕ1<0 时,yt 倾向于在正负值之间上下浮动。

• MA项表示
  一个q阶的预测误差回归模型可以表示如下：
  
  c是常数项，εt是随机误差项。
  yt 可以看成是历史预测误差的加权移动平均值，q指定了历史预测误差的期数。

• 完整表示
  
  即: 被预测变量Yt = 常数+Y的p阶滞后的线性组合 + 预测误差的q阶滞后的线性组合

ARIMA模型定阶

看图定阶

差分阶数d

• 如果时间序列本身就是平稳的，就不需要差分，所以此时d=0。
• 如果时间序列不平稳，那么主要是看时间序列的acf图，如果acf表现为10阶或以上的拖尾，那么需要进一步的差分，如果acf表现为1阶截尾，则可能是过度差分了，最好的差分阶数是使acf先拖尾几阶，然后截尾。
• 有的时候，可能在2个阶数之间无法确定用哪个，因为acf的表现差不多，那么就选择标准差小的序列。
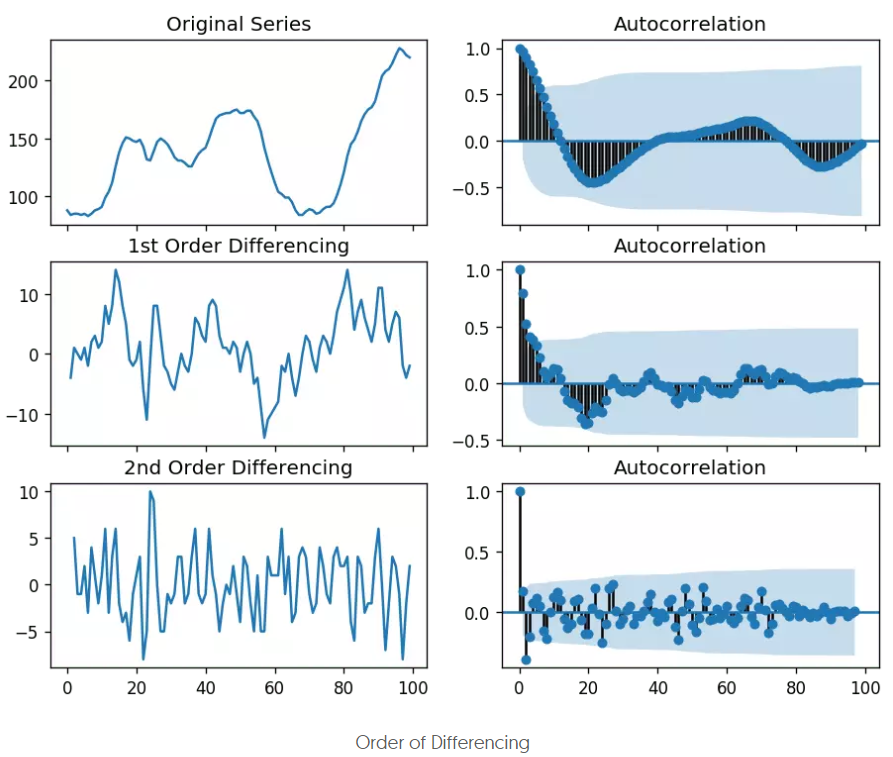
• 下面是原时间序列、一阶差分后、二阶差分后的acf图：
  
  可以看到，原序列的acf图的拖尾阶数过高了，而二阶差分后的截尾阶数过小了，所以一阶差分更合适。

python代码：

import numpy as np, pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize':(9,7), 'figure.dpi':120})

# Import data : Internet Usage per Minute
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/wwwusage.csv', names=['value'], header=0)

# Original Series
fig, axes = plt.subplots(3, 2, sharex=True)
axes[0, 0].plot(df.value); axes[0, 0].set_title('Original Series')
plot_acf(df.value, ax=axes[0, 1])

# 1st Differencing
axes[1, 0].plot(df.value.diff()); axes[1, 0].set_title('1st Order Differencing')
plot_acf(df.value.diff().dropna(), ax=axes[1, 1])

# 2nd Differencing
axes[2, 0].plot(df.value.diff().diff()); axes[2, 0].set_title('2nd Order Differencing')
plot_acf(df.value.diff().diff().dropna(), ax=axes[2, 1])

plt.show()

AR阶数p

AR的阶数p可以通过pacf图来设定，因为AR各项的系数就代表了各项自变量x对因变量y的偏自相关性。

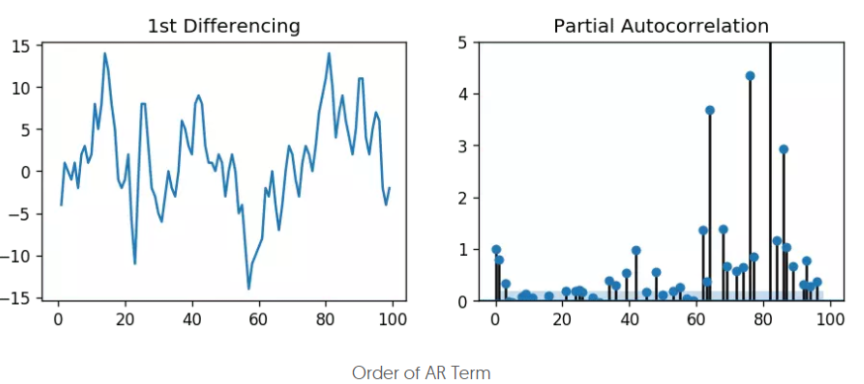
可以看到，lag1，lag2之后，偏自相关落入了蓝色背景区间内，表示不相关，所以这里阶数可以选择2，或者保守点选择1。

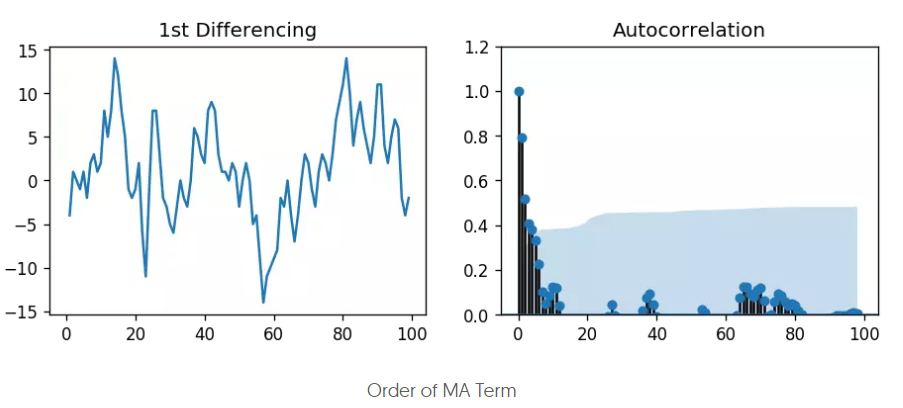
MA阶数q

MA阶数通过acf图来设定，因为MA是预测误差，预测误差是自回归预测和真实值之间的偏差。定阶过程类似AR阶数的设定过程。这里可以选择3，或者保守点选择2。

信息准则定阶

• AIC(Akaike Information Criterion)
  
  L是数据的似然函数，k=1表示模型考虑常数c，k=0表示不考虑。最后一个1表示算上误差项，所以其实第二项就是2乘以参数个数。

• AICc（修正过的AIC）
  

• BIC(Bayesian Information Criterion)
  

注意事项：

• 信息准则越小，说明参数的选择越好，一般使用AICc或者BIC。
• 差分d，不要使用信息准则来判断，因为差分会改变了似然函数使用的数据，使得信息准则的比较失去意义，所以通常用别的方法先选择出合适的d。
• 信息准则的好处是可以在用模型给出预测之前，就对模型的超参做一个量化评估，这对批量预测的场景尤其有用，因为批量预测往往需要在程序执行过程中自动定阶。

构建ARIMA模型

from statsmodels.tsa.arima_model import ARIMA

# 1,1,2 ARIMA Model
model = ARIMA(df.value, order=(1,1,2))
model_fit = model.fit(disp=0)
print(model_fit.summary())

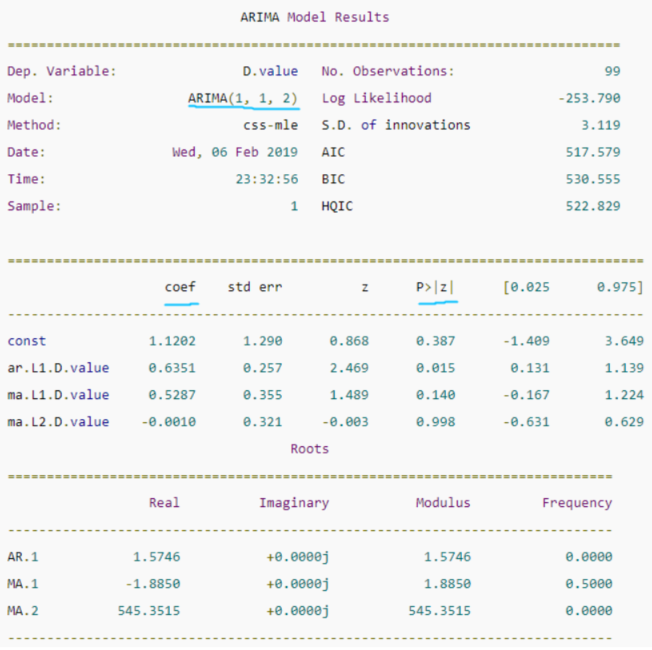
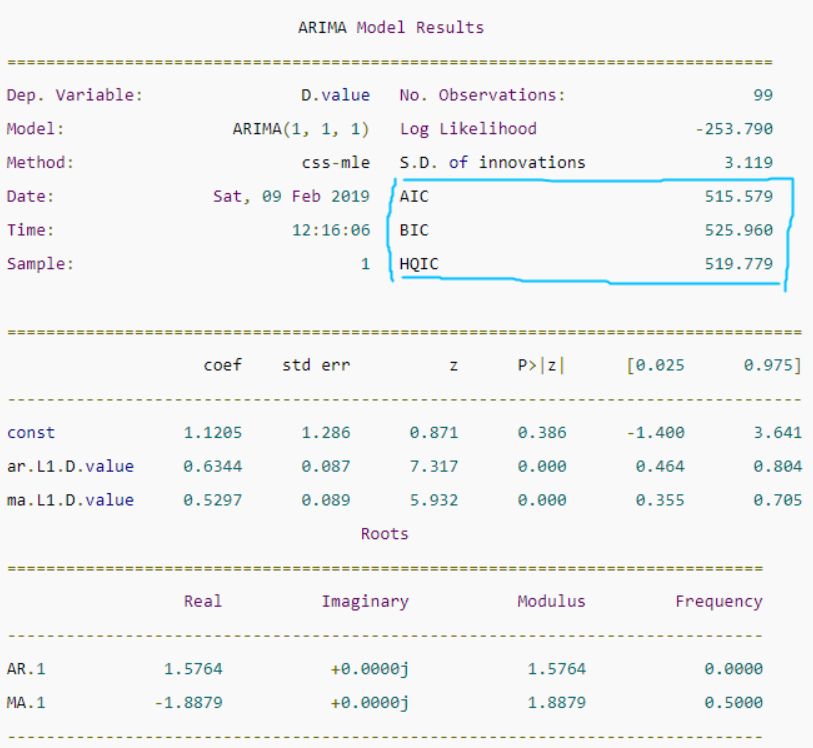
中间的表格列出了训练得到的模型各项和对应的系数，如果系数很小，且‘P>|z|’ 列下的P-Value值远大于0.05，则该项应该去掉，比如上图中的ma部分的第二项，系数是-0.0010,P-Value值是0.998,那么可以重建模型为ARIMA(1,1,1)，从下图可以看到，修改阶数后的模型的AIC等信息准则都有所降低：

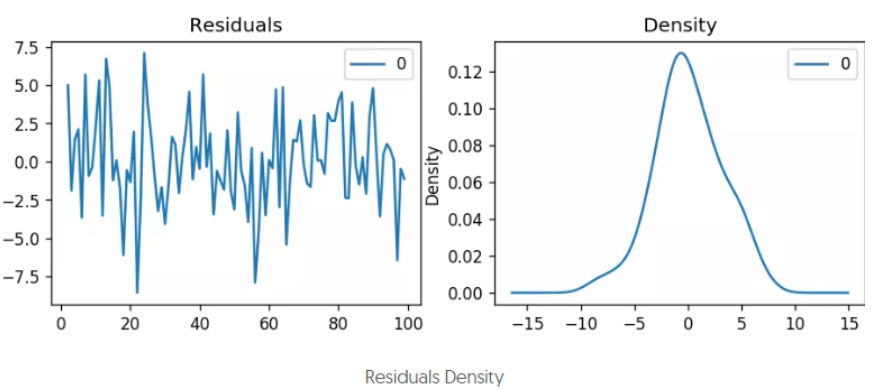
检查残差

通常会检查模型拟合的残差序列，即训练数据原本的序列减去训练数据上的拟合序列后的序列。该序列越符合随机误差分布(均值为0的正态分布)，说明模型拟合的越好，否则，说明还有一些因素模型未能考虑。

• python实现：

# Plot residual errors
residuals = pd.DataFrame(model_fit.resid)
fig, ax = plt.subplots(1,2)
residuals.plot(title="Residuals", ax=ax[0])
residuals.plot(kind='kde', title='Density', ax=ax[1])
plt.show()

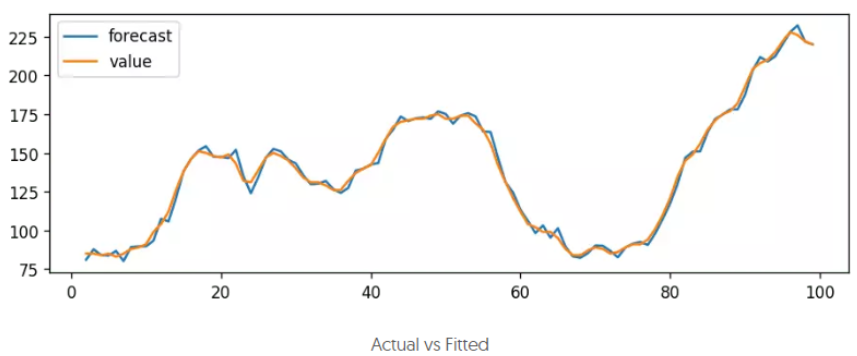
模型拟合

# Actual vs Fitted
model_fit.plot_predict(dynamic=False)
plt.show()

模型预测

除了在训练数据上拟合，一般都会预留一部分时间段作为模型的验证，这部分时间段的数据不参与模型的训练。

from statsmodels.tsa.stattools import acf

# Create Training and Test
train = df.value[:85]
test = df.value[85:]

# Build Model
# model = ARIMA(train, order=(3,2,1))  
model = ARIMA(train, order=(1, 1, 1))  
fitted = model.fit(disp=-1)  

# Forecast
fc, se, conf = fitted.forecast(15, alpha=0.05)  # 95% conf

# Make as pandas series
fc_series = pd.Series(fc, index=test.index)
lower_series = pd.Series(conf[:, 0], index=test.index)
upper_series = pd.Series(conf[:, 1], index=test.index)

# Plot
plt.figure(figsize=(12,5), dpi=100)
plt.plot(train, label='training')
plt.plot(test, label='actual')
plt.plot(fc_series, label='forecast')
plt.fill_between(lower_series.index, lower_series, upper_series, 
                 color='k', alpha=.15)
plt.title('Forecast vs Actuals')
plt.legend(loc='upper left', fontsize=8)
plt.show()

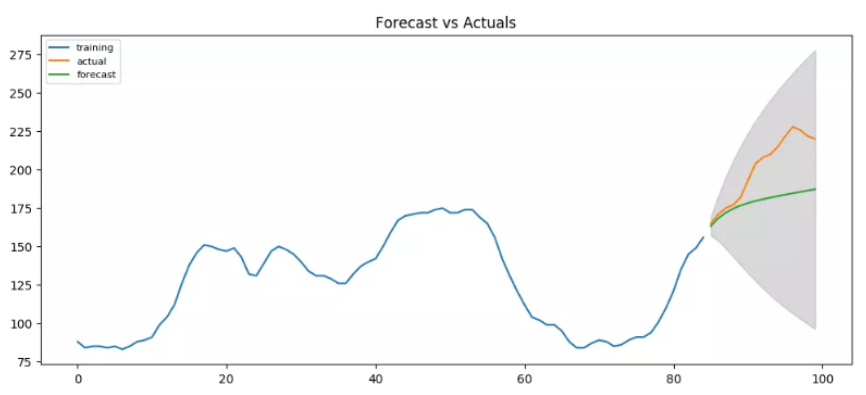
这是在ARIMA(1,1,1)下的预测结果，给出了一定的序列变化方向，看上去还是可以的。不过所有的预测值，都在真实值以下，所以还可以试试看有没有别的更好的阶数组合。
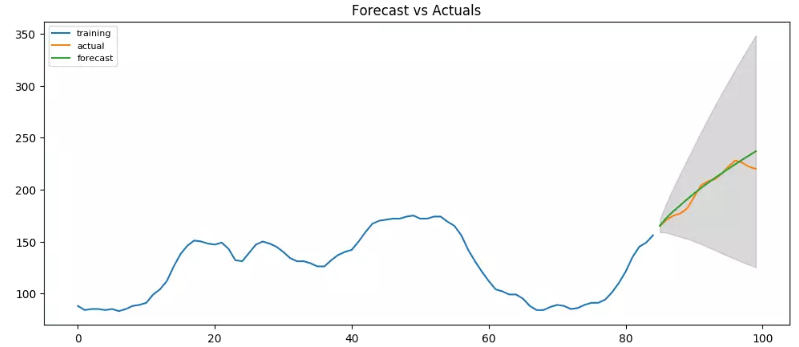
其实如果尝试用ARIMA(3,2,1)会发现预测的更好：

AUTO ARIMA

通过预测结果来推断模型阶数的好坏毕竟还是耗时耗力了些，一般可以通过计算AIC或BIC的方式来找出更好的阶数组合。pmdarima模块的auto_arima方法就可以让我们指定一个阶数上限和信息准则计算方法，从而找到信息准则最小的阶数组合。

from statsmodels.tsa.arima_model import ARIMA
import pmdarima as pm

df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/wwwusage.csv', names=['value'], header=0)

model = pm.auto_arima(df.value, start_p=1, start_q=1,
                      information_criterion='aic',
                      test='adf',       # use adftest to find optimal 'd'
                      max_p=3, max_q=3, # maximum p and q
                      m=1,              # frequency of series
                      d=None,           # let model determine 'd'
                      seasonal=False,   # No Seasonality
                      start_P=0, 
                      D=0, 
                      trace=True,
                      error_action='ignore',  
                      suppress_warnings=True, 
                      stepwise=True)

print(model.summary())

# Forecast
n_periods = 24
fc, confint = model.predict(n_periods=n_periods, return_conf_int=True)
index_of_fc = np.arange(len(df.value), len(df.value)+n_periods)

# make series for plotting purpose
fc_series = pd.Series(fc, index=index_of_fc)
lower_series = pd.Series(confint[:, 0], index=index_of_fc)
upper_series = pd.Series(confint[:, 1], index=index_of_fc)

# Plot
plt.plot(df.value)
plt.plot(fc_series, color='darkgreen')
plt.fill_between(lower_series.index, 
                 lower_series, 
                 upper_series, 
                 color='k', alpha=.15)

plt.title("Final Forecast of WWW Usage")
plt.show()

从输出可以看到，模型采用了ARIMA(3,2,1)的组合来预测，因为该组合计算出的AIC最小。

如何自动构建季节性ARIMA模型？

如果模型带有季节性，则除了p,d,q以外，模型还需要引入季节性部分：

与非季节性模型的区别在于，季节性模型都是以m为固定周期来做计算的，比如D就是季节性差分，是用当前值减去上一个季节周期的值，P和Q和非季节性的p,q的区别也是在于前者是以季节窗口为单位，而后者是连续时间的。
上节介绍的auto arima的代码中，seasonal参数设为了false，构建季节性模型的时候，把该参数置为True，然后对应的P，D，Q,m参数即可，代码如下：

# !pip3 install pyramid-arima
import pmdarima as pm
# Seasonal - fit stepwise auto-ARIMA
smodel = pm.auto_arima(data, start_p=1, start_q=1,
                         test='adf',
                         max_p=3, max_q=3, m=12,
                         start_P=0, seasonal=True,
                         d=None, D=1, trace=True,
                         error_action='ignore',  
                         suppress_warnings=True, 
                         stepwise=True)
smodel.summary()

注意这里的stepwise参数，默认值就是True，表示用stepwise algorithm来选择最佳的参数组合，会比计算所有的参数组合要快很多，而且几乎不会过拟合，当然也有可能忽略了最优的组合参数。所以如果你想让模型自动计算所有的参数组合，然后选择最优的，可以将stepwise设为False。

如何在预测中引入其它相关的变量？

在时间序列模型中，还可以引入其它相关的变量，这些变量称为exogenous variable(外生变量，或自变量)，比如对于季节性的预测，除了之前说的通过加入季节性参数组合以外，还可以通过ARIMA模型加外生变量来实现，那么这里要加的外生变量自然就是时间序列中的季节性序列了(通过时间序列分解得到)。需要注意的是，对于季节性来说，还是用季节性模型来拟合比较合适，这里用外生变量的方式只是为了方便演示外生变量的用法。因为对于引入了外生变量的时间序列模型来说，在预测未来的值的时候，也要对外生变量进行预测的，而用季节性做外生变量的方便演示之处在于，季节性每期都一样的，比如年季节性，所以直接复制到3年就可以作为未来3年的季节外生变量序列了。

def load_data():
    """
    航司乘客数时间序列数据集
    该数据集包含了1949-1960年每个月国际航班的乘客总数。
    """
    from datetime import datetime
    date_parse = lambda x: datetime.strptime(x, '%Y-%m-%d')
    data = pd.read_csv('https://www.analyticsvidhya.com/wp-content/uploads/2016/02/AirPassengers.csv', index_col='Month', parse_dates=['Month'], date_parser=date_parse)
    # print(data)
    # print(data.index)
    ts = data['value']
    # print(ts.head(10))
    # plt.plot(ts)
    # plt.show()
    return ts,data

# 加载时间序列数据
_ts,_data = load_data()
# 时间序列分解
result_mul = seasonal_decompose(_ts[-36:],  # 3 years
                                model='multiplicative',
                                freq=12,
                                extrapolate_trend='freq')
_seasonal_frame = result_mul.seasonal[-12:].to_frame()
_seasonal_frame['month'] = pd.to_datetime(_seasonal_frame.index).month
# seasonal_index = result_mul.seasonal[-12:].index
# seasonal_index['month'] = seasonal_index.month.values
print(_seasonal_frame)
_data['month'] = _data.index.month
print(_data)
_df = pd.merge(_data, _seasonal_frame, how='left', on='month')
_df.columns = ['value', 'month', 'seasonal_index']
print(_df)
print(_df.index)
_df.index = _data.index  # reassign the index.
print(_df.index)

build_arima(_df,_seasonal_frame,_data)

# SARIMAX Model
sxmodel = pm.auto_arima(df[['value']],
						exogenous=df[['seasonal_index']],
						start_p=1, start_q=1,
						test='adf',
						max_p=3, max_q=3, m=12,
						start_P=0, seasonal=False,
						d=1, D=1, trace=True,
						error_action='ignore',
						suppress_warnings=True,
						stepwise=True)
sxmodel.summary()
# Forecast
n_periods = 36
fitted, confint = sxmodel.predict(n_periods=n_periods,
								  exogenous=np.tile(seasonal_frame['y'].values, 3).reshape(-1, 1),
								  return_conf_int=True)
index_of_fc = pd.date_range(data.index[-1], periods = n_periods, freq='MS')
# make series for plotting purpose
fitted_series = pd.Series(fitted, index=index_of_fc)
lower_series = pd.Series(confint[:, 0], index=index_of_fc)
upper_series = pd.Series(confint[:, 1], index=index_of_fc)

# Plot
plt.plot(data['y'])
plt.plot(fitted_series, color='darkgreen')
plt.fill_between(lower_series.index,
				 lower_series,
				 upper_series,
				 color='k', alpha=.15)

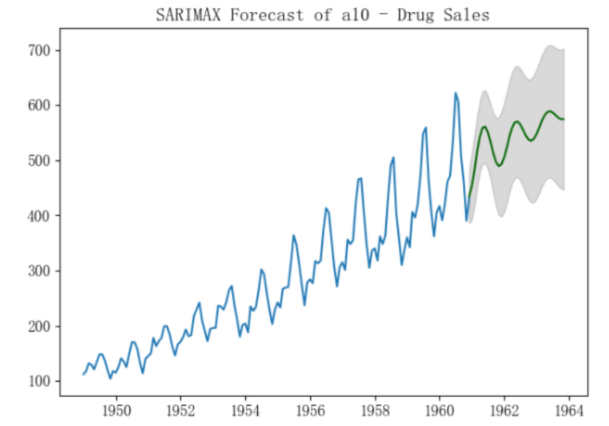
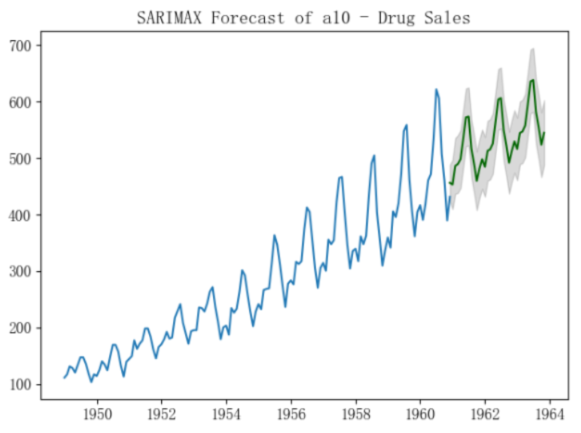
plt.title("SARIMAX Forecast of a10 - Drug Sales")
plt.show()

以下是结果比较:

• 选择ARIMA(3,1,1)来预测：
  
• 选择季节性模型SARIMA(3,0,1),(0,1,0,12)来预测:
  
• 选择带季节性外生变量的ARIMA(3,1,1)来预测:
  

ok,本篇就这么多内容啦~，下一篇将基于一个实际的例子来介绍完整的预测实现过程，感谢阅读O(∩_∩)O。