吴恩达 MachineLearning Week8
知识点概述
1. K - means 算法
K - means 算法用于解决聚类问题,属于无监督学习。可以对没有标记的数据进行处理,将其分成 K 类。其步骤如下:
- 从数据集随机选择 K 个作为起始的均值点
- 计算每个点到各个均值点的距离,并将点归类到距离最近的点类中。(假设 x 点到 m ( m <= K) 号点距离最短,则 x 归为第 m 类)
- 计算各个类的平均值( 即把被分到各个类的 x 相加除以类中 x 的个数)将新的坐标作为新的均值点
- 从 2 开始重复直到收敛
- 从 1 开始重复 ,最后取收敛点到各类点之合最小的一组
2. PLA( Principal Component Analysis )
用于将数据降维,加快模型的处理和计算速度。其步骤如下:
1. 计算参数sigma:
![]()
其中 X 是输入数据的矩阵。
2. 将参数带入公式:
![]()
得到的 U 为一个 N * N 的矩阵 , S 是一个对角矩阵(除了主对角线以外数据全都是0)
假设我们要降到 K 维,则取矩阵 U 的前 K 列,得到U_reduce(n * k) 将 X 和 U_reduce 相乘得到新的矩阵 Z ,就是降后的矩阵,用来代替X
3. 将 Z 和 U_reduce 的转置相乘,可以得到还原矩阵 X_approx,我们有如下公式
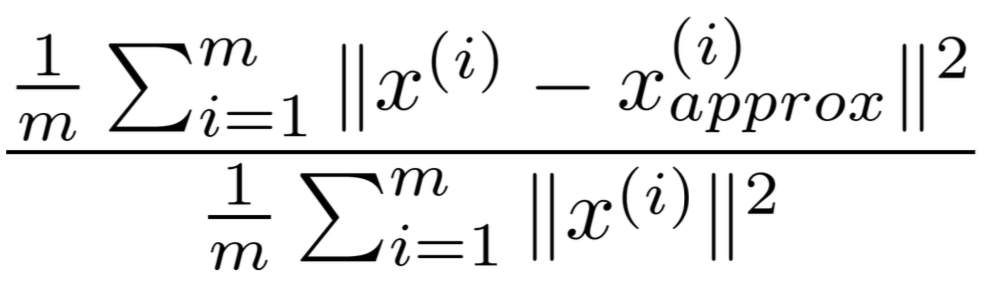
这个值越小,说明降维对原数据造成的影响越小,这个值一般要在 0.01 ~ 0.1之间。而利用 S 矩阵可以很方便的计算这个值。公式:
1 - ![]()
k 即要取的 K 维。我们要找一个 k 值,使得该值小于一定值。
课后练习题代码
pca.m
function [U, S] = pca(X) %PCA Run principal component analysis on the dataset X % [U, S, X] = pca(X) computes eigenvectors of the covariance matrix of X % Returns the eigenvectors U, the eigenvalues (on diagonal) in S % % Useful values [m, n] = size(X); % You need to return the following variables correctly. U = zeros(n); S = zeros(n); % ====================== YOUR CODE HERE ====================== % Instructions: You should first compute the covariance matrix. Then, you % should use the "svd" function to compute the eigenvectors % and eigenvalues of the covariance matrix. % Sigma = (X' * X) / m ; [U , S , V] = svd(Sigma); % ========================================================================= end
projectData.m
function Z = projectData(X, U, K) %PROJECTDATA Computes the reduced data representation when projecting only %on to the top k eigenvectors % Z = projectData(X, U, K) computes the projection of % the normalized inputs X into the reduced dimensional space spanned by % the first K columns of U. It returns the projected examples in Z. % % You need to return the following variables correctly. Z = zeros(size(X, 1), K); % ====================== YOUR CODE HERE ====================== % Instructions: Compute the projection of the data using only the top K % eigenvectors in U (first K columns). % For the i-th example X(i,:), the projection on to the k-th % eigenvector is given as follows: % x = X(i, :)'; % projection_k = x' * U(:, k); % Z = X * U(: , 1:K); % ============================================================= end
recoverData.m
function X_rec = recoverData(Z, U, K) %RECOVERDATA Recovers an approximation of the original data when using the %projected data % X_rec = RECOVERDATA(Z, U, K) recovers an approximation the % original data that has been reduced to K dimensions. It returns the % approximate reconstruction in X_rec. % % You need to return the following variables correctly. X_rec = zeros(size(Z, 1), size(U, 1)); % ====================== YOUR CODE HERE ====================== % Instructions: Compute the approximation of the data by projecting back % onto the original space using the top K eigenvectors in U. % % For the i-th example Z(i,:), the (approximate) % recovered data for dimension j is given as follows: % v = Z(i, :)'; % recovered_j = v' * U(j, 1:K)'; % % Notice that U(j, 1:K) is a row vector. % X_rec = Z * U(: , 1:K)'; % ============================================================= end
findClosestCentroids.m
function idx = findClosestCentroids(X, centroids)
%FINDCLOSESTCENTROIDS computes the centroid memberships for every example
% idx = FINDCLOSESTCENTROIDS (X, centroids) returns the closest centroids
% in idx for a dataset X where each row is a single example. idx = m x 1
% vector of centroid assignments (i.e. each entry in range [1..K])
%
% Set K
K = size(centroids, 1);
% You need to return the following variables correctly.
idx = zeros(size(X,1), 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Go over every example, find its closest centroid, and store
% the index inside idx at the appropriate location.
% Concretely, idx(i) should contain the index of the centroid
% closest to example i. Hence, it should be a value in the
% range 1..K
%
% Note: You can use a for-loop over the examples to compute this.
%
m = size(X , 1);
for i = 1 : m
x = X(i , :);
min = sum((x - centroids(1 , :)) .^ 2);
idx(i) = 1;
for j = 2 : K
sumnum = sum((x - centroids(j , :)) .^ 2);
if sumnum < min
min = sumnum;
idx(i) = j;
end
end
end
% =============================================================
end
computeCentroids.m
function centroids = computeCentroids(X, idx, K)
%COMPUTECENTROIDS returns the new centroids by computing the means of the
%data points assigned to each centroid.
% centroids = COMPUTECENTROIDS(X, idx, K) returns the new centroids by
% computing the means of the data points assigned to each centroid. It is
% given a dataset X where each row is a single data point, a vector
% idx of centroid assignments (i.e. each entry in range [1..K]) for each
% example, and K, the number of centroids. You should return a matrix
% centroids, where each row of centroids is the mean of the data points
% assigned to it.
%
% Useful variables
[m n] = size(X);
% You need to return the following variables correctly.
centroids = zeros(K, n);
% ====================== YOUR CODE HERE ======================
% Instructions: Go over every centroid and compute mean of all points that
% belong to it. Concretely, the row vector centroids(i, :)
% should contain the mean of the data points assigned to
% centroid i.
%
% Note: You can use a for-loop over the centroids to compute this.
%
cnt = zeros(K , n);
for i = 1 : m
centroids(idx(i) , :) = centroids(idx(i) , :) + X(i , :)
cnt(idx(i) , :) = cnt(idx(i) , :) + 1;
end
centroids = centroids ./ cnt;
% =============================================================
end