海明码,又称汉明码,是一种线性纠错码,用于纠正数据。
奇偶校验
我们常听的数据校验,莫过于奇偶校验了。
假设数据传过来01010101, 那么其中有1位作为校验位,如果数据中包含有奇数个1的话,则将奇偶位设定为1;反之,如果数据中有偶数个1的话,则将奇偶位设定为0。
但是这个显然只能知道出错了,但是无法定位具体是哪一位出错了,因此海明码出现了!
海明码
我们用更多的位,作为校验位。
我们有一个公式(如果我们需要一次传输 n 位数据,那么这时候需要 k 为校验位):2^k - 1 >= n + k
显然,我们输入 n,我们就能算出 k 的值。
举个栗子
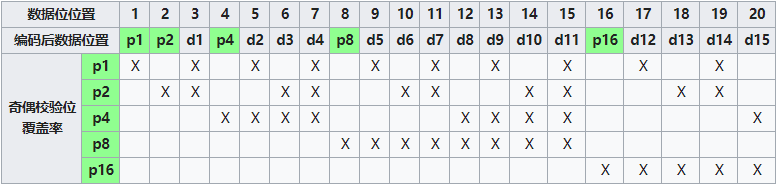
例如下图,我们需要传 15 位数据,套上公式(2^k - 1 >= 15 + k), 算出来 k 最小是 5 才满足。
就是说这个时候,我们需要 5 为校验位;包括数据和校验位,总共会发出去 20 位。
标志位的位置
我们看到图中,标绿的地方就是我们的校验位,这些校验位并不是从1号位排到5号位这么简单,而是专门挑选 2^p 位来放置。
我们把标志位设为 p1、p2、p4、p8、p16
这是为了让标志位能最大程度地表示出编号:p1 * 2^0 + p2 * 2^1 + p4 * 2^2 + p8 * 2^3 + p16 * 2^4,这 5 个校验位的组合不同,不会出现重复的结果
如果直接把校验位从1排到5,那就变成这样:p1 * 2^0 + p2 * 2^1 + p4 * (2^0 + 2^1) + p8 * 2^2 + p16 * (2^0 + 2^2),这 5 个校验位的组合不同会出现重复的结果
标志位的含义
既然 这 5 个校验位各自表示着 1 个编号位,我们看下图
p1 代表了 二进制编号中第一位为 1 的位(第1、3、5、7、9、11、13、15、17、19位)
p2 代表了 二进制编号中第二位为 1 的位(第2、3、6、7、10、11、14、15、18、19位)
.....
每一个校验位 px 的值就是对代表的这些位(除掉其中的校验位),进行异或的结果
p1 = d1 ⊕ d2 ⊕ d4 ⊕ d5 ⊕ d7 ⊕ d9 ⊕ d11 ⊕ d12 ⊕ d14
p2 = d1 ⊕ d3 ⊕ d4 ⊕ d6 ⊕ d7 ⊕ d10 ⊕ d11 ⊕ d13 ⊕ d14
...
至此,数据就已经准备好了,可以发送过来了。然而知道现在,我们的主角海明码还没出现 。莫急等我继续说。
异或
我们知道异或,是2个2进制位的一种运算,相同取0,不相同取1。
再算一遍校验位
我们客户端接收到了上面 1 ~ 20 号的信息,用所有数据位再算一遍,按校验位的策略再算一次校验位,得到 p1'、p2'、p4'、p8'、p16'。
得到海明码
s1 = p1' ⊕ p1
s2 = p2' ⊕ p2
s3 = p4' ⊕ p4
s4 = p8' ⊕ p8
s5 = p16' ⊕ p16
如果 s1 ~ s5 有出现非0,则表示有数据位出错了。
而 s1 ~ s5 组成的编号,就是具体出错的那个位了!!