20172324 2018-2019-1 《程序设计与数据结构》第七周学习总结

20172324 2018-2019-1 《程序设计与数据结构》第七周学习总结

教材学习内容总结

概述

1. 二叉查找树是一种含有附加属性的二叉树，即其左孩子小于父节点，而父节点又小于等于其右孩子。

   它是特殊的二叉树：对于二叉树，假设x为二叉树中的任意一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。那么，这棵树就是二叉查找树。如下图所示：
   

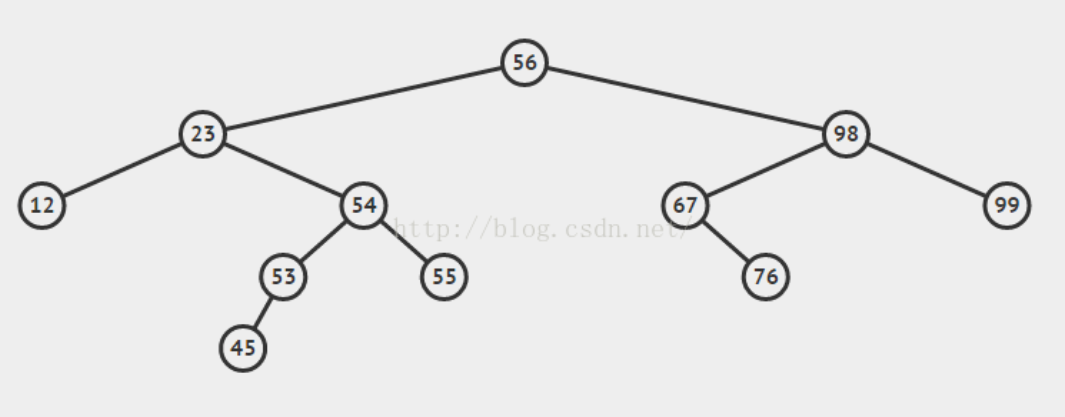
   在二叉查找树中：
   (01) 若任意节点的左子树不空，则左子树上所有结点 的值均小于它的根结点的值；
   (02) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
   (03) 任意节点的左、右子树也分别为二叉查找树。
   (04) 没有键值相等的节点（no duplicate nodes）。

2. 二叉查找树的接口类继承自二叉树的接口类BinaryTreeADT，在其基础上补充了一些操作方法

操作	说明
addElement	往树中添加一个元素
removeElement	从树中删除一个元素
removeAllOccurrences	从树中删除所指定元素的任何存在
removeMin	删除树中最小元素
removeMax	删除树中最大元素
findMin	返回一个指向树中的最小元素的引用
findMax	返回一个指向树中的最大元素的引用

链表实现二叉查找树

• 每个BinaryTreeNode对象要维护一个指向结点所存储元素的引用，另外还要维护指向结点的每个孩子的引用。
• LinkedBinarySearchTree类提供了两个构造函数

//创建空的LinkedBinarySearchTree
public LinkedBinarySearchTree()
{
      super();
}
//创建一棵根结点为特定元素的LinkedBinarySearchTree
public LinkedBinarySearchTree(T element)
  {
      super(element);

      if (!(element instanceof Comparable))
          throw new NonComparableElementException("LinkedBinarySearchTree");
  }

• addElement操作：根据二叉查找树的性质，插入一个节点的时候，如果根节点为空，就此节点作为根节点，如果根节点不为空，就要先和根节点比较，如果比根节点的值小，就插入到根节点的左子树中，如果比根节点的值大就插入到根节点的右子树中，如此递归下去，找到插入的位置。

  例图(插入65，黄色线为比较的轨迹)：

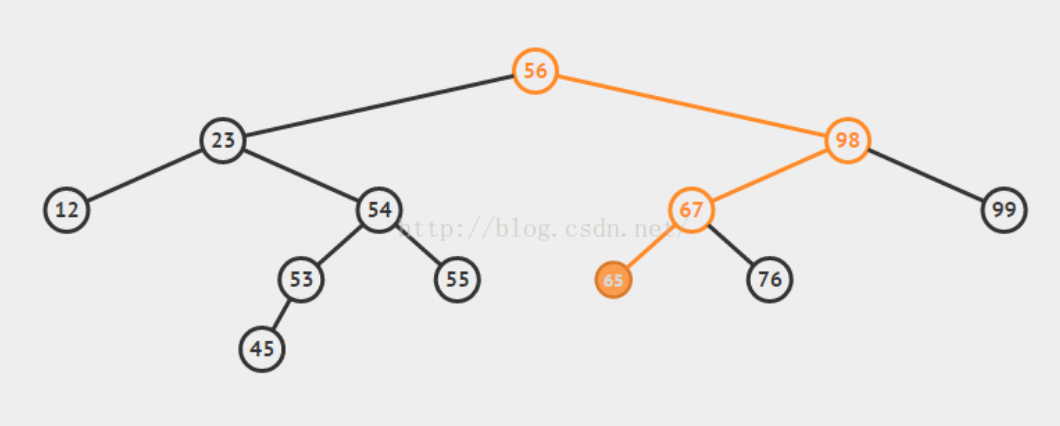
• removeElement操作：
  初始状态：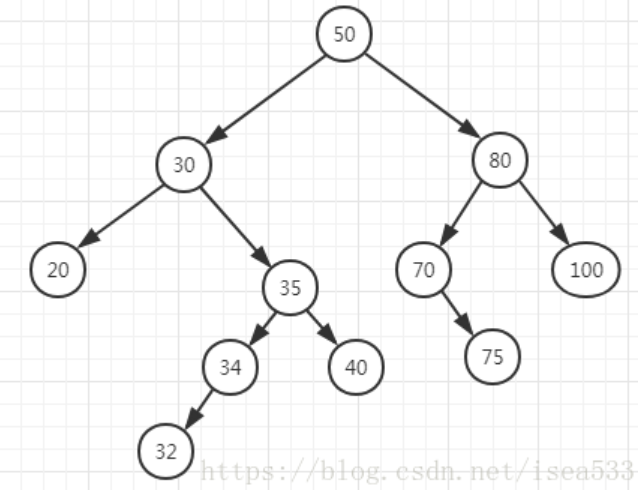

  1. 被删除的节点只有左节点或者只有右节点，这种情况好办，因为节点在一条链上，没有分叉，就像处理链表一样把这个节点摘掉就行了。让它的父节点关联它的子节点，它的子节点关联它的父节点就完事。如果它没有父节点，说明它是根节点，直接将其子节点作为根节点就行。
     满足这个情况的节点有 34, 70 两个节点，这里以 70 为例，如下图所示：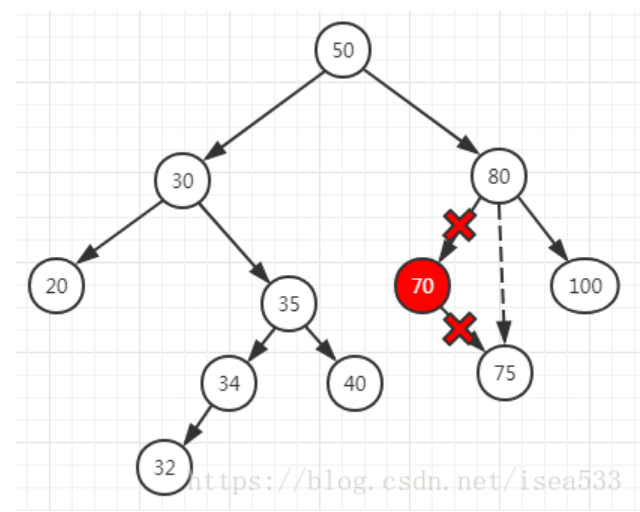
     删除 70 的时候，需要断两个关系，然后建立父节点和子节点的关系，经过上述操作后，节点状态如下图所示：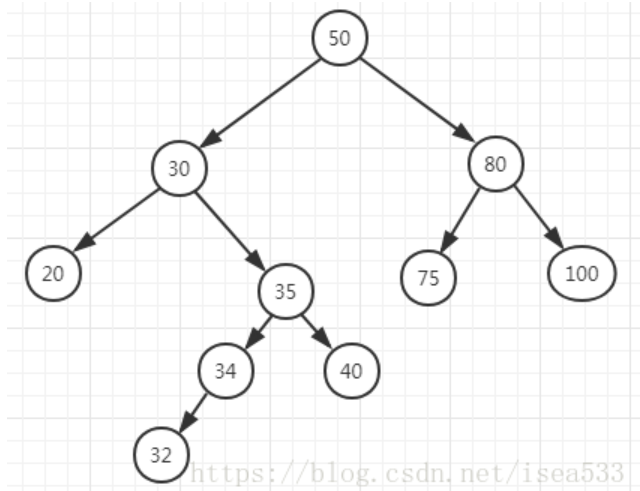

  2. 被删除的节点没有子节点，这种情况也很简单，它是叶子节点，直接置空，将其父节点对应的子节点也置空，就完事。
     在我们图中，符合这个条件的有 20,32,40,75,100，随便找个 20 来演示删除该节点：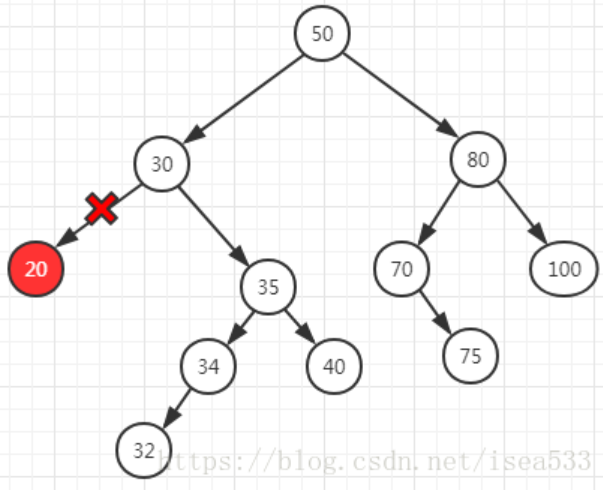
     这种情况是最简单的，我们只需要删除该节点和父节点的关系即可。删除的时候需要先判断自己和父节点的关系是左侧还是右侧，如果父节点的左节点是自己，就清左侧，否则就是右侧。删除后如下图所示：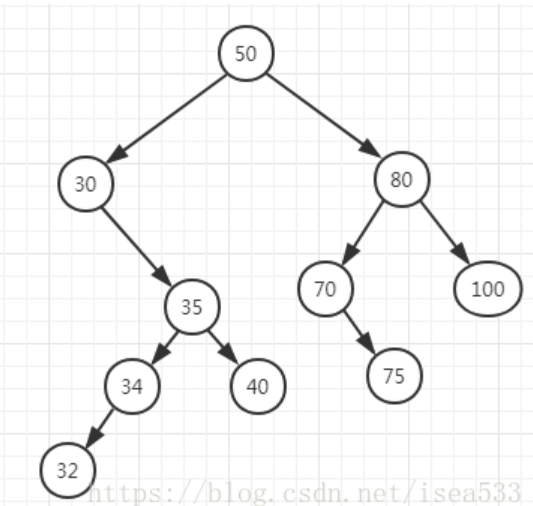

  3. 被删除的节点有左右子节点。树结构中的所有节点按顺序拍好的话，它的前驱和它的后继两个节点刚好在它左右紧挨着它。当一个节点被删除时，为了保证二叉树的结构不被破坏，要让它的前驱或者后继节点来代替它的位置，然后将它的前驱或者后继节点同样做删除操作。
     满足同时存在左右节点的节点有 50,30,80,35 这 4 个节点，30 看起来更复杂，我们以 30 为例。
     当二叉查找树以中序遍历时，遍历的结果是一个从小到大排列的顺序，如下图所示：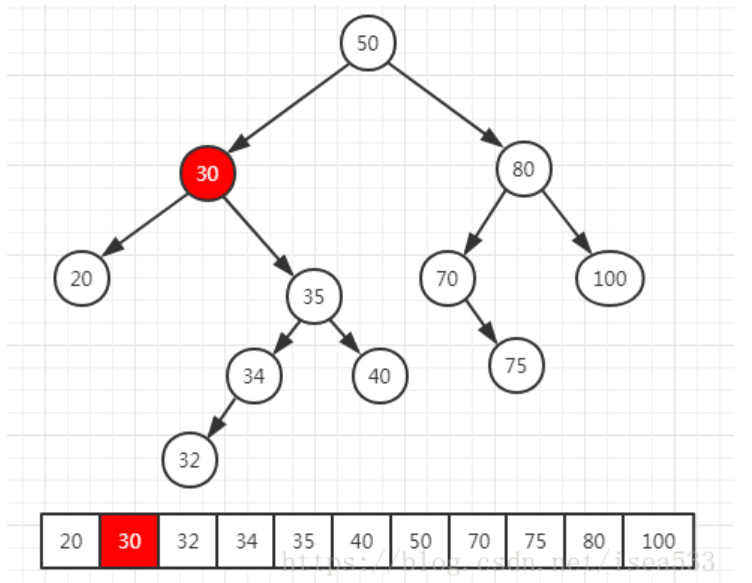
     当我们删除 30 节点的时候，整个中序遍历的结果中，从 32 开始都往前移动了一位。32 是 30 的后继节点，就是比 30 大的节点中最小的节点。当某个节点存在右节点时，后继结点就是右节点中的最小值，由于左侧节点总比右侧节点和父节点小，所以后继节点一定没有左节点。从这一个特点就能看出来，后继结点有可能存在右节点，也有可能没有任何节点。后继结点还有一个特点，就是他比 30 的左节点大，比 30 所有的右节点都小，因此删除 30 的时候，可以直接将后继结点 32 的值（key）转移到 30 节点上，然后删除后继结点 32。由于后继结点最多只有一个子节点，因此删除后继节点时，就变成了 3 种情况中的前两种。图示如下：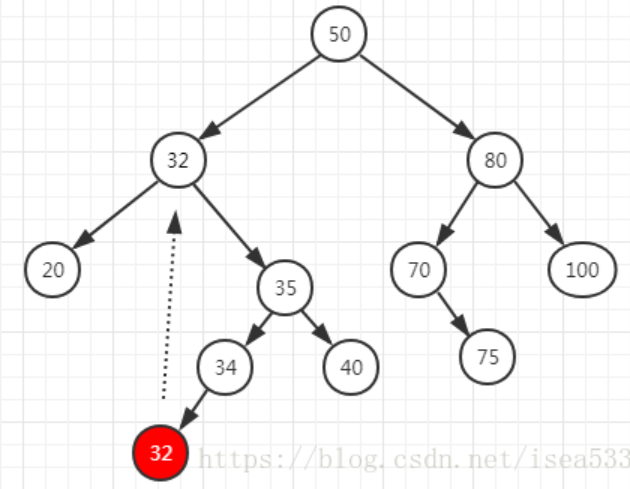

• removeAllOccurrences操作：可以看做调用了removeElement,当在树中找不到指定元素是，则抛出ElementNotFoundException异常，如果指定的元素不是Comparable，则removeAllOccurrences方法也会抛出ClassCaseException异常。只要树中还含有目标元素，就会再次调用removeElement方法。

• removeMin操作：最小元素在树中位置的3种情形：

  1. 树根没有左孩子，树根即为最小元素，树根右孩子变成新的根结点；
  2. 树的最左侧结点为一片叶子，该叶子即为最小元素，设置其父结点的左孩子应用为null；
  3. 树的最左侧结点为内部结点，设置其父结点的左孩子引用指向最小元素的右孩子。

用有序列表实现二叉查找树

列表的一些常见操作：

操作	说明	LinkedList	BinarySearchTreeList
removeFirst	删除列表的首元素	O(1)	O(logn)
removeLast	删除列表的末元素	O(n)	O(logn)
remove	删除列表中的一个特定元素	O(n)	O(logn)
first	考察列表前端的那个元素	O(1)	O(logn)
last	考察列表末端的那个元素	O(n)	O(logn)
contains	判断列表是否含有一个特定元素	O(n)	O(logn)
is Empty	判定列表是否为空	O(1)	O(1)
size	判定列表中的元素数目	O(1)	O(1)

有序列表特有的操作：

操作	说明	LinkedList	BinarySearchTreeList
add	向列表添加一个元素	O(n)	O(logn)

平衡二叉查找树

如果没有平衡假设，它的效率比链表的还低，因为每个结点还附带额外的开销。

• AVL树的旋转规律:

1. LL型

   平衡二叉树某一节点的左孩子的左子树上插入一个新的节点，使得该节点不再平衡。这时只需要把树向右旋转一次即可，如图所示，原A的左孩子B变为父结点，A变为其右孩子，而原B的右子树变为A的左子树，注意旋转之后Brh是A的左子树
   

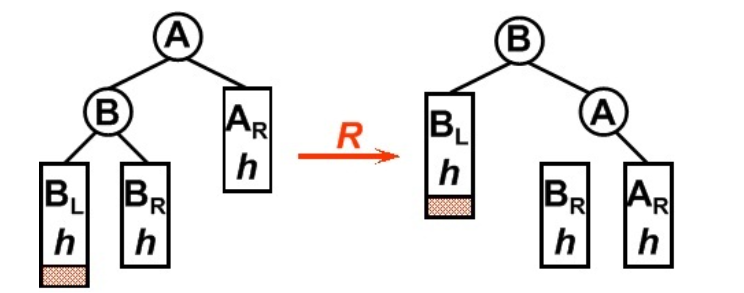
2. RR型

   平衡二叉树某一节点的右孩子的右子树上插入一个新的节点，使得该节点不再平衡。这时只需要把树向左旋转一次即可，如图所示，原A右孩子B变为父结点，A变为其左孩子，而原B的左子树Blh将变为A的右子树。
   

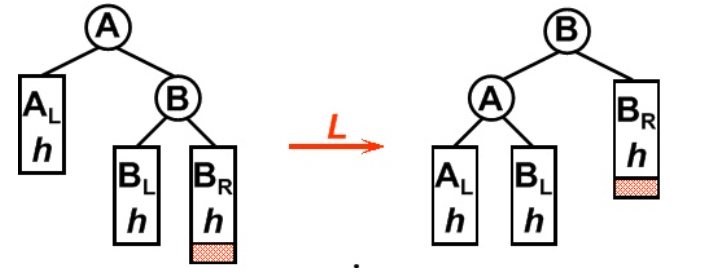
3. LR型

平衡二叉树某一节点的左孩子的右子树上插入一个新的节点，使得该节点不再平衡。这时需要旋转两次，仅一次的旋转是不能够使二叉树再次平衡。如图所示，在B节点按照RR型向左旋转一次之后，二叉树在A节点仍然不能保持平衡，这时还需要再向右旋转一次。

4. RL型

平衡二叉树某一节点的右孩子的左子树上插入一个新的节点，使得该节点不再平衡。同样，这时需要旋转两次，旋转方向刚好同LR型相反。

• 实现二叉查找树：AVL树
  • 平衡因子：右子树的高度减去左子树的高度。

比较	平衡因子<-1	平衡因子>1
孩子的平衡因子<=-1	右旋	右左旋
孩子的平衡因子>=1	左右旋	左旋

• 实现二叉查找树：红黑树

红黑树的特性:

1. 每个节点或者是黑色，或者是红色。
2. 根节点是黑色。
3. 每个叶子节点（Null）是黑色。 [注意：这里叶子节点，是指为空(NULL)的叶子节点！]即每个空结点为黑色，也即默认结点为黑色
4. 如果一个节点是红色的，则它的子节点必须是黑色的。
5. 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

（接下来的部分都让我处于神游状态，先把王老师的讲解粘下来吧）

红黑树-插入:





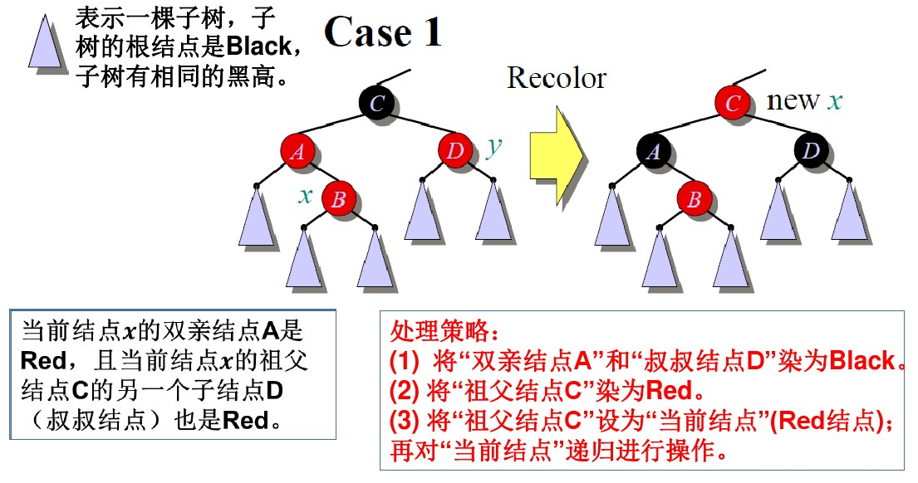
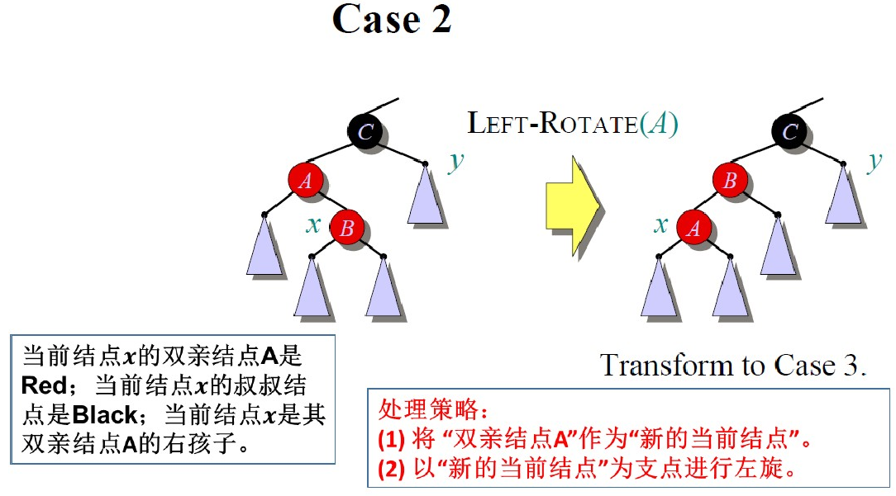
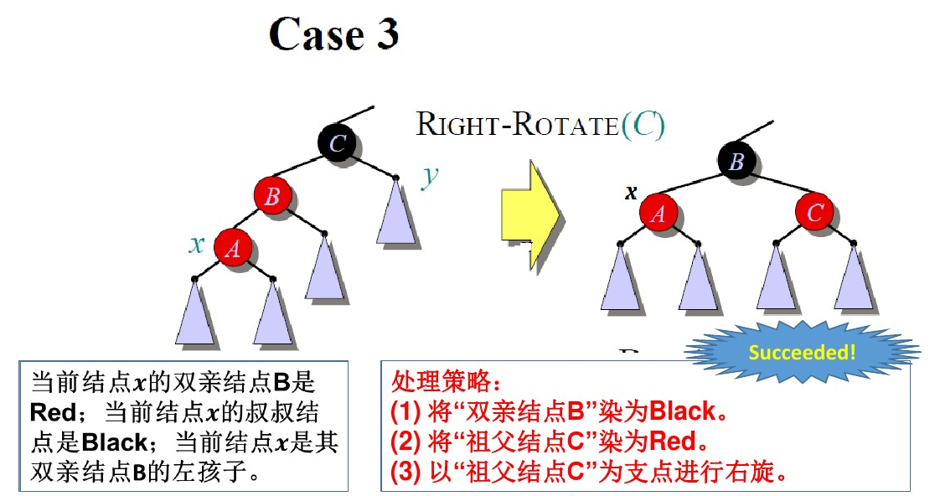
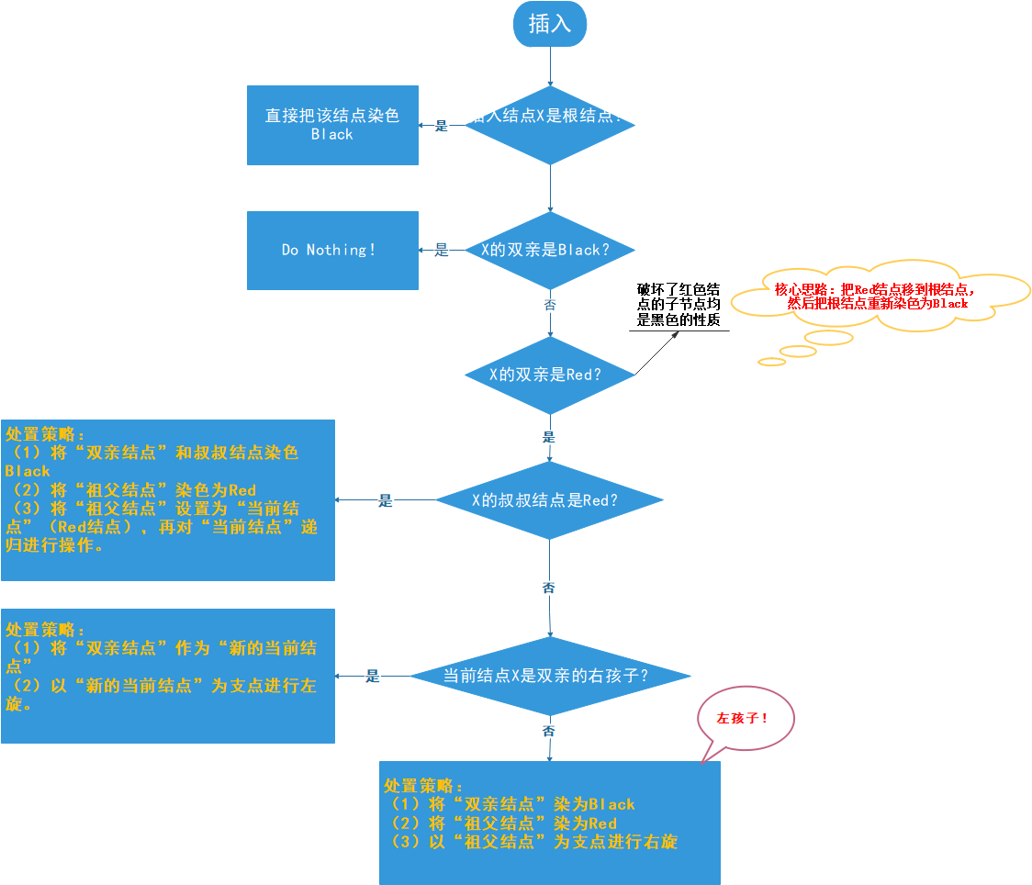
红黑树-删除：

过于复杂 放在教材学习问题中

教材学习中的问题和解决过程

• 问题1：根据二叉查找树的定义，下面这个图是否正确？
  

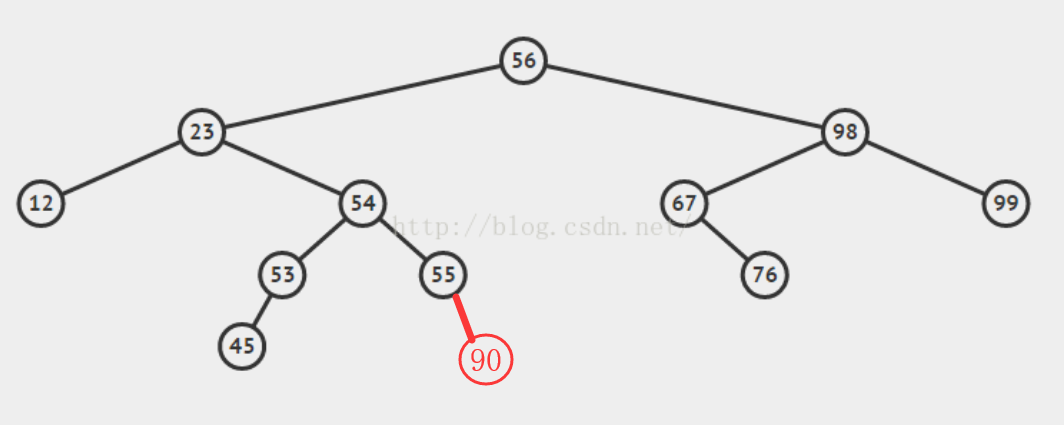
• 问题1解决方案：不正确，虽然它作为右子树满足大于等于它的父节点这一个要求，但它仍然是根结点左子树。90大于56了，所以不满足。可以放在99的左子树

• 问题2：红黑树的删除

• 问题2解决方案：我以为我会懂，但是我没有，先放个博客链接在这里，以后慢慢理解红黑树的删除（算法导论）

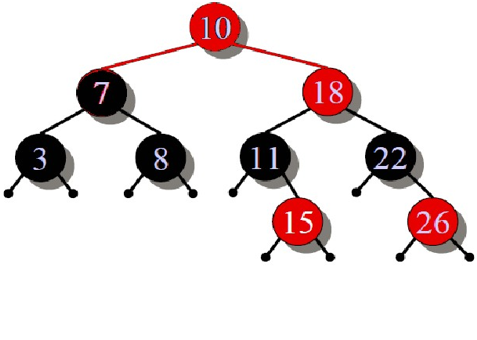
• 问题3：在课上提出来的一个问题，如下图所示，该二叉树不满足红黑二叉树，一种方法是将10重新染色成黑色，再将7染色成红色。现在问题来，能不能把10和18都染成黑色？
  

• 问题3解决方案：还在讨论中

代码托管

上周考试错题总结

无错题

点评过的同学博客和代码

• 本周结对学习情况
  • 结对同学学号21
  • 本周结对学习情况
    内容详略得当；
    代码调试环节比较详细，出现得问题都差不多

其他（感悟、思考等，可选）

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	0	1/1	20/20
第二周	300/500	1/2	18/38
第三周	300/600	1/3	18/38
第四周	400/1000	2/5	18/38
第五周	300/1300	1/6	18/38
第六周	300/1300	3/9	18/38
第七周	300/1300	3/9	18/38

参考资料

• 《Java程序设计与数据结构（第四版）》
• 二叉查找树(三)之 Java的实现
• 红黑树的删除（算法导论）