一、jupyter notebool介绍
Jupyter Notebook是Ipython的升级版,而Ipython可以说是一个加强版的交互式 Shell,也就是说,它比在terminal里运行python会更方便,界面更友好,功能也更强大。
二、安装
pip install jupyter #打开jupyter notebook 也只需要在终端输入:win + R jupyter notebook
然后浏览器就显示下面的界面:

在dos窗口运行jupyter notebook后出现:cannot import name 'create_prompt_application'的错误,这是因为你的python安装的prompt_toolkit版本是2.0以上,而ipython依赖的是1.5.0版本的prompt_toolkit
import prompt_toolkit print(prompt_toolkit.__version__) #'2.0.7'
你只需要pip uninstall 2.0版本的prompt_toolkit,然后安装1.5.0的即可
https://pypi.org/project/prompt_toolkit/1.0.15/#files
下面介绍在Linux上安装jupyter:
pip install jupyter
1)生成配置文件
jupyter notebook --generate-config
2)打开ipython,生成密码
ipython from notebook.auth import passwd passwd() Enter password: Verify password:
需要记住密码并复制一下生成的密文
3)修改配置文件
vim ~/.jupyter/jupyter_notebook_config.py
c.NotebookApp.ip='*' # 就是设置所有ip皆可访问
c.NotebookApp.password = u'sha:ce...刚才复制的那个密文'
c.NotebookApp.open_browser = False # 禁止自动打开浏览器
c.NotebookApp.port =8888 #随便指定一个端口
c.NotebookApp.allow_remote_access = True #允许远程登录
4)启动jupyter
jupyter notebook

5)在windows采用ip+端口号访问即可
通常情况下需要你输入密码,该密码即为你之前通过notebook设置的密码。请熟知
三、使用
1.新建
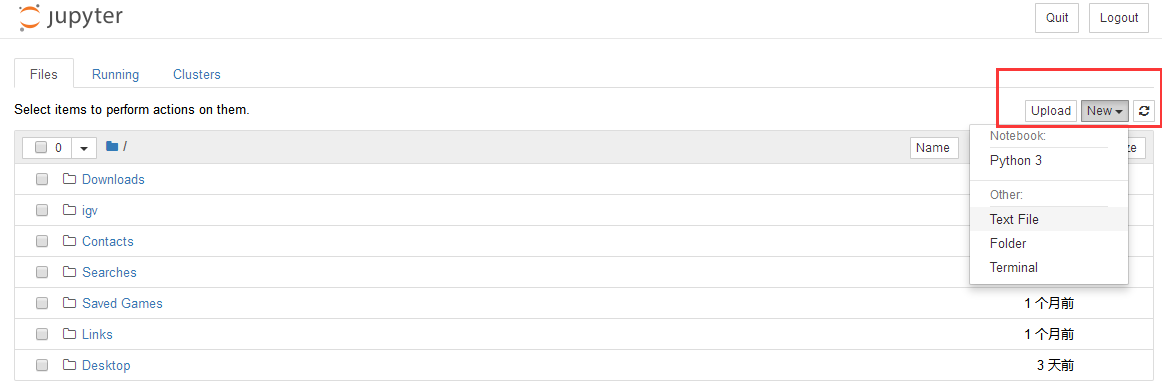
2.点击Python3
出现框叫做单元格,你可以把你的代码分成一段段的单元格输入,然后可以逐个单元格地运行。注意,这个功能是非常友好的,有时候只修改了中间的一小段代码,又不想全部代码都要重新运行的时候这个功能就非常有用了。
另外,单元格是可以改变顺序的。而且可以输出图片和绘图!
3.重命名,下载文档
可以点击Untitled也可以点击File-rename,下载的话点击File-Download as,其中下载格式很多,可以行尝试。
4.保存
Ctrl + S,默认是保存为ipynb,保存在你的主目录下!
5.删除某个cell
将光标停留在待删除的cell内,按下ESC进入命令模式,然后按两次d键即可删除该cell
6.显示行号
点击View-Toggle Line Numbers
7.撤销删除
点击esc后按z键
8.删除选中的行(也可以是一行)
光标停在某一行(或者选中多行),然后ctrl + D