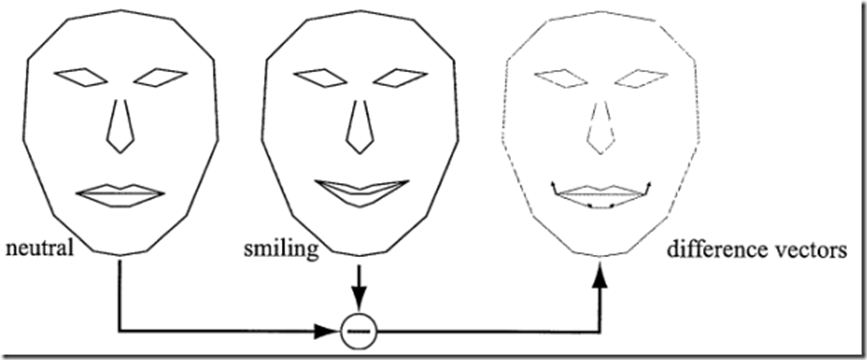
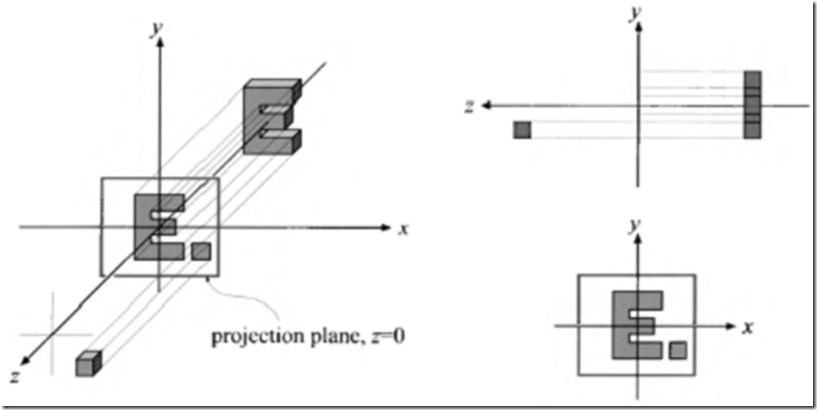
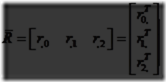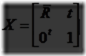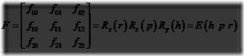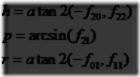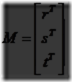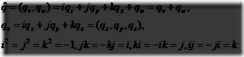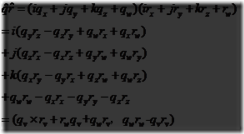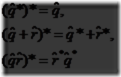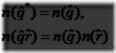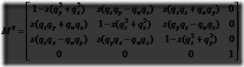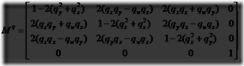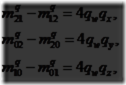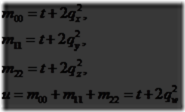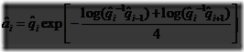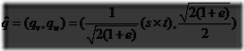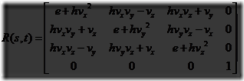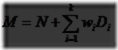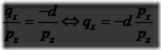图形变换是一个将例如点、向量或者颜色等实体进行某种转换的操作。对于计算机图形学的先驱者,掌握图形变换是极为重要的。有了他们,你就可以对象、光源以及摄像机进行定位,变形以及动画添加。你也可以确认所有的计算都是在同一个坐标系统下面进行的,而物体以不同的方式投影到平面上。在图形变换只有少数操作运行,但它们足以证明图形变换在实时图形学中的重要性,甚至可以说是任何一种计算机图形学。
线性变换是一种保留了向量加法和标量乘法的变换。具体如下:
f(x) + f(y) = f(x+y), kf(x) = f(kx) (4.1)
例如,f(x)=5x就是变换,即将向量中的每个元素都乘以5。这种变换是线性的,因为两个向量先乘以5再相加的出的结果与它们先相加后乘以5的结果是一样的。标量乘法条件是满足的。这个函数叫做缩放变换,因为它改变了对象的缩放比例(尺寸)。使向量绕原点转动的旋转变换是另一种线性变换。缩放和旋转变换,以及所有用于三元向量的线性变换,都可以用一个3×3的矩阵表示。
然而,这个矩阵的大小还不够。用于三元向量x的函数,例如f(x)=x+(7,3,2)不是线性的。分别在两个向量上运行这个函数时,会将(7,3,2)中的每个元素都加两次而形成结果。将一个固定数值的向量加到另一个向量上是执行了平移,即是,它以同样的大小移动所有位置。这是一种十分有用的变换类型,而我们希望将各种变换组合到一起,例如,将对象缩小至一半,移动它到不同的位置。目前为止保持函数的简单形式,使得很难将它们组合起来。
线性变换和平移的结合可以通过仿射变换实现,典型的是将其存储在一个4×4的矩阵中。仿射变换执行线性变换,接着进行平移。为代表四元向量,我们使用以同样方法(粗体小写)指示点和方向的齐次标记。v = (vx vy vz 0)T代表一个方向向量,而v = (vx vy vz 1)T代表一个点。在这一章,我们会大量使用到附录A中解释的术语。你现在或许需要看看附录,特别是905页的关于齐次标记的A.4章节。
所有的平移,旋转,缩放,反射,以及剪切矩阵都是仿射的。仿射矩阵的主要特点是它保持了直线间的平行关系,但不一定保持其长度和角度。一个仿射变换也可以多个个体仿射变换的任意次序的连接。
这一章节将从最基本的,最基础的仿射变换开始。这确实是很基本的,并且这章节可以看着简单转换的“参考手册”。然后更多的是关于专用矩阵的描述,接着的是一个强大的图形变换工具——四元数的描述。然后是顶点混合和变形,这两者都是简单但功能强大的网格的动画表示方式。最后,投影矩阵被描述。大部分的图形变换,他们的符号,函数和属性将在表格4.1中总结。
图形变换是一个操纵几何图形的基本工具。所有的图形应用程序编程接口(APIs)包含了矩阵操作,这些操作实现了很多这章所讨论的图形变换。但是去了解真正的矩阵,以及它们在函数调用背后的互动是值得的。知道在函数调用后矩阵做了什么只是一个开始,但理解矩阵本身的属性会让你更为深入。例如,当你正处理正交的矩阵时,这些理解能帮助你认识到它的逆矩阵也就是它的转置矩阵(见904页),从而得出更快的矩阵求逆。这类知识可以优化代码,加速执行。
|
符号 |
名称 |
特性 |
|
T(t) |
平移矩阵 |
移动一个点。 仿射。 |
|
Rx(ρ) |
旋转矩阵 |
绕x轴旋转ρ的角度。相似的标记用于y轴和z轴。 正交且仿射。 |
|
R |
旋转矩阵 |
所有的旋转矩阵。 正交且仿射。 |
|
S(s) |
缩放矩阵 |
根据s,沿x、y、z轴进行缩放。 仿射。 |
|
Hij(s) |
剪切矩阵 |
相对j对i进行参数为s的剪切变形,i, j∈{x, y, z}。 仿射。 |
|
E(h, p, r) |
欧拉变换 |
欧拉角(head/yaw,pitch,roll)给出的朝向矩阵。 仿射。 |
|
Po(s) |
正交投影 |
向某个平面或体积进行平行投影。 仿射。 |
|
Pp(s) |
透视投影 |
向一个平面或体积进行透视投影。 |
|
slerp() |
插值变换 |
根据四元数和以及参数t,创建一个插值的四元数 |
表格4.1 这一章中讨论的大部分图形变换的总结
4.1 基本图形变换
这一节描述了最基本的图形变换,例如平移,旋转,缩放,剪切,图形变换的连结,刚体转换,法线变换(这并不常见),和矩阵求逆。对于已有相应经验的读者,这可以用作简单图形变换的参考手册;而对于新手,它可以用作该主题的入门。这些材料是这章剩余部分以及本书中其它各章的必须的背景知识。我们从最简单的变换——平移变换开始。
4.1.1 平移
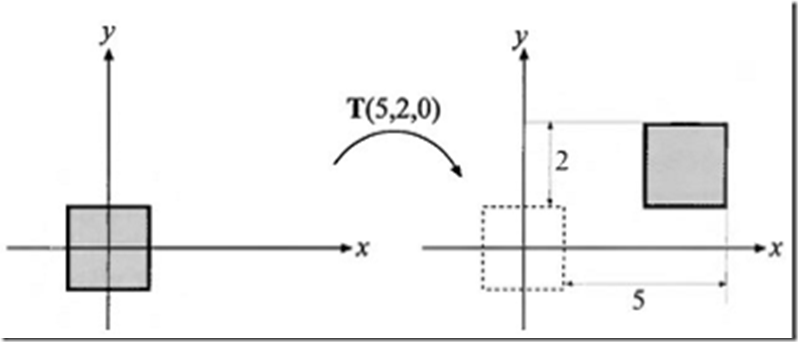
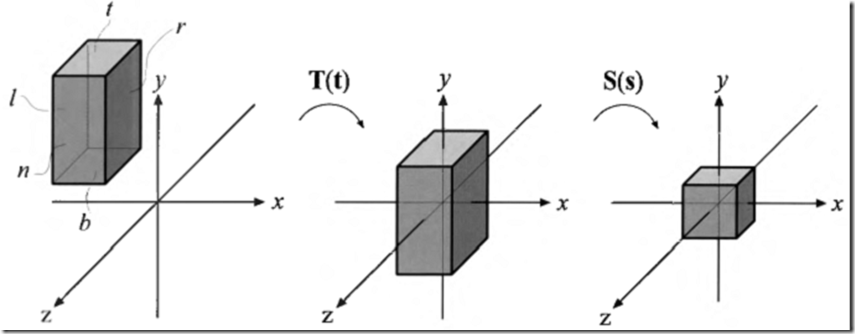
由一个位置到其他位置的变换是由平移矩阵,T所代表。这个矩阵通过一个向量t=(tx,ty,tz)变换一个实体。下面的方程4.2给出T:
图4.1展示了平移变换产生的效果。容易看到的是一个点P=(px, py, pz, 1)与T(t)相乘产生新的点P’=(px+tx, py+ty, pz+tz, 1),这就是平移。注意到向量v=(vx, vy, vz, 0)左乘T后没有变化,因为一个方向向量不能被平移。相反的,其余的仿射变换都能影响点和向量。平移矩阵的逆矩阵是T-1(t)=T(-t),换句话说,向量t是取反的。
图4.1 左边的一个正方形被平移矩阵T(5,2,0)所转换,据此,正方形向右移动了5个单元而向上移动了2个单元。
4.1.2 旋转
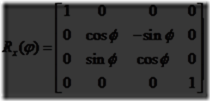
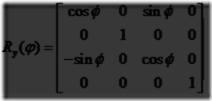
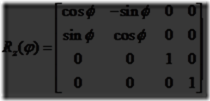
一个旋转变换绕给定的过原点的轴将一个向量(位置或方向)旋转给定的角度。就像平移变换那样,它是刚体变换,也就是它保存被变换的点之间的距离,并且保持旋向性(也就是说他从不会使图形左右交换)。这两种图形变换在计算机图形学中的物体的定位和定向是十分有用的。一个方向矩阵是一个与摄像机视图或者一个定义其在空间中的朝向的对象相关的旋转矩阵,也就是说他的方向是向上和向前。常用的旋转矩阵是Rx(φ),Ry(φ)和Rz(φ),它们使实体绕相应的x,y和z轴转动φ个弧度。方程4.3~4.5给出了相应的矩阵:
对于每个3×3的旋转矩阵,R,绕任何轴旋转φ弧度,它的迹(定义见898页)是独立于轴的常量,计算如下:
tr(R) = 1 + 2cosφ (4.6)
可以在62页的图4.4看到旋转矩阵的效果。Ri(φ)表征一个旋转矩阵,除了它绕i轴转动φ个弧度外,它还保持i轴上所有的点不变。注意到R也用于指示绕任意轴的旋转矩阵。上面给出的轴旋转矩阵可用于一系列的三个图形变换去执行绕任意轴的旋转。这个过程将在4.2.1节中讨论。4.2.4节中直接涵盖了执行一个绕任意轴的旋转。
所有的旋转矩阵行列式为1并且是正交的,十分容易通过904页的附录A给出的正交矩阵定义去验证。对于任意数量的这种变换的连接,这个性质也是保持的。这是另一个获得逆矩阵的方法:Ri-1(φ) = Ri(-φ),也就是,绕同一轴的相反方向转动。因为旋转矩阵是正交,其行列式总是为1.
例子:绕一个点旋转。假设我们想让一个对象以z轴为轴,以某个点P为旋转中心,旋转φ弧度。这是什么图形变换?这个情景在图4.2中描绘。因为一个绕一点的旋转的特点是点本身事实上不能被旋转所影响,于是图形变换首先平移对象,通过T(-p)使得P与原点重合。其后接着的是真正的旋转:Rz(φ)。最后,对象使用T(p)被平移回原来的位置。产生的变换,X,如下
X=T(p)Rz(φ)T(-p) (4.7)
图4.2 绕指定点P旋转的例子。
4.1.3 缩放
一个缩放矩阵,S(s)=S(sx, sy, sz),根据对应x,y和z轴的因子sx,sy,sz缩放一个实体。这意味着一个缩放矩阵可以用于物体的放大缩小。si(i∈{x, y, z})越大,缩放的实体在相应的方向就越大。将S的任何分量设置为1通常避免该方向发生缩放变化。方程4.8展示了S:
62页的图4.4展示了缩放矩阵的效果。如果sx=sy=sz则将缩放操作叫做一致的,否则就是不一致的。有时会用各向同性和各向异性代替一致的和不一致的。其逆矩阵为S-1(s)=S(1/sx, 1/sy, 1/sz)。
另一个使用齐次坐标创建一个一致的缩放矩阵的合法方法是操纵矩阵中位于(3,3)位置的元素,也就是右下角的元素。这个数字影响齐次坐标的w分量,因此所有的坐标都通过矩阵进行缩放变换。例如,一致地以因子5进行缩放,(0,0),(1,1)(2,2)位置上的元素可以设置为5,或者(3,3)位置上的元素设置为1/5。执行这个操作的两个不同矩阵如下:
与将S用于一致缩放相反,S’的使用必须遵守均匀化,缩放要一致。这可能是低效的,因为它在均匀化过程中涉及了除法;如果右下角((3,3)位置)的元素为1,则不需要相除。当然,如果系统总是执行除法而不先测试除数为1,那么这里就没有额外的消耗。
一或三个S分量为一负值给出了反射矩阵,也叫做镜像矩阵。如果只有两个缩放因子是-1,那么我们会旋转π个弧度。当发现反射矩阵时,通常需要特殊处理。例如,一个顶点顺序是逆时针的三角形经过反射变换后会得到顺时针顺序。这个顺序的改变会导致不正确的光照和背部消隐产生。为检测一个给定矩阵是属于那种情况,计算左上3×3的元素组成的矩阵的行列式。如果数值是负的,矩阵就是反射的。
例子:某个方向上的缩放。缩放矩阵S仅沿着x,y和z轴进行缩放。如果需要在其他方向上进行缩放,那么就需要复合变换了。假设需要沿着标准正交的,右手定则的向量fx,fy和fz进行缩放。首先,如下构建矩阵F:
其思路是使这三个轴给出的坐标系与标准的轴重合,接着使用标准的缩放矩阵,然后再转换回来。第一步通过与F的转置矩阵,也就是逆矩阵,相乘而得出。方程4.11展示了这个变换:
X=FS(s)FT (4.11)
4.1.4 剪切变换
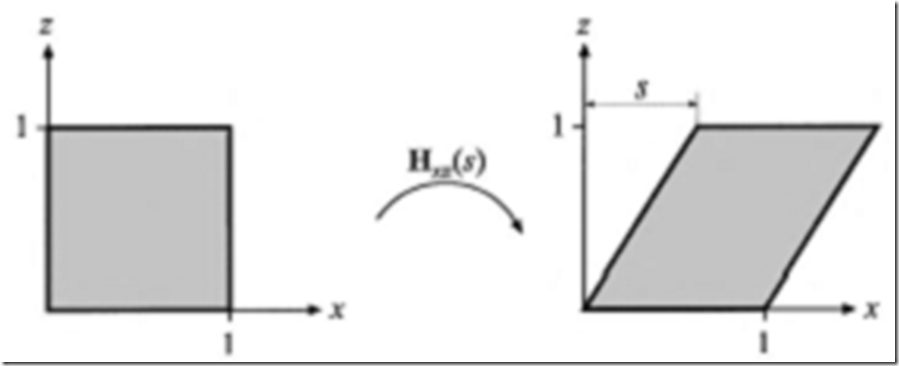
另一类图形变换是一组剪切矩阵。它们可以做,例如被用于游戏中去扭曲场景中的实体以营造迷幻的效果或是通过抖动创造模糊反射(见9.3.1节)。这有6种基本的剪切矩阵,它们被标记为Hxy(s),Hxz(s),Hyx(s),Hyz(s),Hzx(s)和Hzy(s)。第一个下标用于标记那个坐标被剪切矩阵改变,而第二个下标指出那个坐标执行这个剪切。方程4.12展示了剪切矩阵Hxz(s)。观察到下标可以用于确定参数s在下面矩阵的位置;x(其数字索引是0)标记为第0行,而z(其数字索引为2)标记为第2列,所以s定位于那儿:
这个矩阵与一个点P相乘产生一个点:(px+spz py pz)T。图4.3生动地将其展示在单元正方形上。Hij(s)的逆矩阵(相对第j号坐标,剪切第i号坐标,且i≠j)通过反方向的剪切变换生成,即H-1ij(s) = Hij(-s)。
图4.3 使用Hxz(s)剪切单位正方形的效果。y和z的值都没有受到图形变换的影响,而x值则是x的原数值与s与z的乘积的和,使得正方形倾斜。
一些计算机图形学的文章使用稍不同种的剪切矩阵:
但在这里,所有的下标都用于标记被第三个坐标剪切的坐标。这两种不同种类的描述之间的关联是H’ij(s,t)=Hik(s)Hjk(t), k用作第三个坐标的索引。使用何种矩阵是个人的喜好和API是否提供支持。
最后,应该注意到的是任何剪切矩阵的行列式|H|=1,这是一个保存体积不变的图形变换。
4.1.5 图形变换的串接
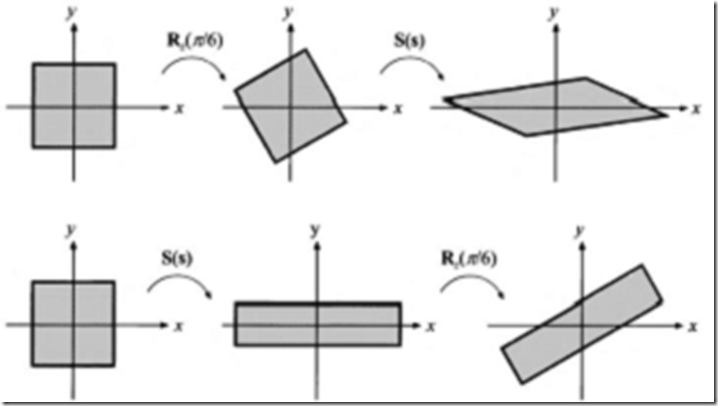
因为矩阵乘法的不可交换性,矩阵出现的顺序变得十分要紧。图形变换的串接因此被认为是依赖于顺序的。
举个顺序依赖的例子,考虑两个矩阵,S和R。S(2,0.5,1)对x进行2倍,对y进行0.5倍的缩放。Rz(π/6)以逆时针绕z轴(其指向从书页面向外)转π/6。这些矩阵可以以两种方式相乘,而产生完全相反的结果。图4.4展示了两个结果。
图4.4 这展示了矩阵相乘时的顺序相关。在上面一行中,旋转矩阵Rz(π/6)被应用,紧接着的是缩放矩阵S(s),其中s=(2, 0.5, 1)。其复合矩阵为S(s)Rz(π/6)。在下面一行中,矩阵以相反的顺序被应用,产生为Rz(π/6)S(s)。两者的结果是明显地不同。对于任意的矩阵M和N,总体上是MN≠NM的。
将一系列矩阵串接合成一个单一矩阵的一个显而易见的原因是效率。例如,想象一下你需要对一个有数千个顶点的对象进行缩放,旋转,以及最后的平移。现在,所有的顶点不是和三个矩阵的每个都相乘,而是三个矩阵串接结合成一个单独的矩阵。这个单独的矩阵被应用在顶点上。这个复合的矩阵C=TRS。注意到这里的顺序:缩放矩阵S将会首先应用在顶点上,因此出现在复合矩阵的右边。这顺序为TRSp=(T(R(Sp)))。
值得注意的是矩阵的串接是顺序相关的,但矩阵可以按需要进行分组。例如,对于TRSp你希望一次计算出刚体运动的图形变换TR。将这两个矩阵分为一组(TR)(Sp),然后用中间结果替换是合法的。因此,矩阵是相关的。
4.1.6 刚体图形变换
当一个人拿一个固体的物体,例如从桌上拿一支钢笔,并且将它移动到另一个位置,例如她衬衫的口袋里,仅仅是物体的朝向和位置发生变换,而物体的形状总体上没有受到影响。这种由平移和旋转串接而组成的图形变换,被称为刚体图形变换,其特点为保持物体的长度,角度和旋向性。
任何刚体矩阵X可以被写成平移矩阵T(t)和旋转矩阵R的串接。因此X形如方程4.14中的矩阵:
X求逆矩阵的计算为X-1=(T(t)R)-1=R-1T(t)-1=RTT(-t),因此,为了计算逆矩阵,左上3×3矩阵R被转置,而T的平移数值改变了符号。这两个新的矩阵以相反的顺序相乘在一起得到逆矩阵。计算X逆矩阵的另一个方法是将R(R为3×3的矩阵)和X认为是如下的标记:
这里,0是一个以0填充的3×1的列向量。产生逆矩阵的一些简单的计算展示在方程4.16的表达式中:
4.1.7 法向图形变换
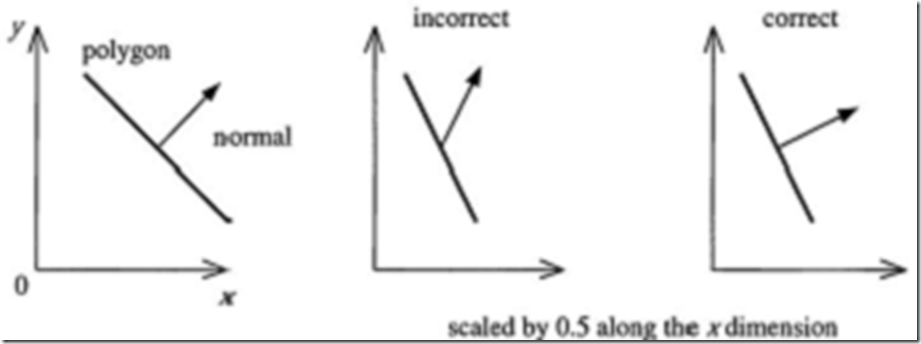
一个单独的矩阵可以用于点,线,多边形和其他几何体的一致变换。同样的矩阵可以变换沿着这些线或多边形表面的切线向量。但是这些矩阵不能用于变换一个重要的图形属性,表面法线(以及顶点光照法线)。图4.5展示了如果同样的矩阵被使用将会发生什么情况。
图4.5 在左边的是原来的几何体,从侧面展示了一个多边形和它的法线。中间的图展示了经过沿x轴进行0.5倍的缩小,而且法线使用同样的矩阵进行变化后图片发生了什么变化。右边的图展示了法线的正确变换。
不是乘以矩阵本身,合适的方法是使用矩阵的伴随矩阵的转置。伴随矩阵的计算在A.3.1节中描述。伴随矩阵总是被认为是存在的。法线在变换以后不保证其为单位长度,因此必须对其标准化。
对于法线变换的传统方法是计算逆矩阵的转置。这个方法通常是可行的。完全求逆(full inverse)是不必要的,但偶尔不能创建。逆矩阵是邻接矩阵除以原矩阵的行列式。如果这个行列式为0,矩阵是奇异的,那么他的逆矩阵就不存在。
即使是计算一个4×4矩阵的邻接矩阵,其运算量也是很大的,而且通常是不需要的。因为法线是一个向量,平移是不会影响它的。此外,多数模型的变换是仿射的。它们不会改变传入的齐次坐标的w分量,也就是说它们不会进行投影。在这些(通常的)环境下,法线变换的计算仅需要计算左上3×3分量的邻接矩阵。
通常甚至这个邻接矩阵也不需要计算。我们知道图形变换矩阵由整个平移,旋转,和整体缩放操作(没有拉伸或压缩)串接而成的。平移不影响法线。整体缩放因子简单地改变法线的长度。剩下的是一系列旋转,它们总是产生某种纯粹的旋转,仅此而已。一个旋转矩阵的特性是它的转置矩阵就是它的逆矩阵。逆矩阵的转置可以用于变换法线,并且两次转置(或者两次求逆)可以互相消去。将这些放在一起,其结果是在这样的环境下,原来的矩阵本身可以直接用于变换法线。
最后,完整的重标准化不总是需要的。如果只是平移和旋转串接在一起,当通过矩阵变换时,法线长度不会变化。如果整体缩放也被串接,那么整体缩放因子(出自4.2.3节)可以直接用于输出法线标准化。例如,如果我们知道一系列的缩放被使用使得对象变为5.2倍大,那么法线变换直接通过这个矩阵,其通过除以5.2实现标准化。或者,要创建一个产生标准化结果的法线变换矩阵的方法是,原来的矩阵左上3×3除以这个缩放因子。
注意到法线变换不是一个问题,在系统中,变换后表面法线源自三角形(例如,三角形的边的叉积)。切线向量与法线在本质上是不同的,而且总是直接被原矩阵所变换。
4.1.8 矩阵求逆
很多的地方需要求逆矩阵,例如,在两个坐标系统中来回变换。基于可得到的图形变换信息,可以使用以下三种计算逆矩阵的方法中的一种。
·如果矩阵是一个单独的图形变换或者一些列带有给定参数的简单变换,那么矩阵可以通过“参数取反”和矩阵的顺序,容易地计算得出。例如,如果M=T(t)R(φ),那么M-1=R(-φ)T(-t)。
·如果已知矩阵是正交的,那么M-1=MT,也就是说转置矩阵就是逆矩阵。任何顺序的旋转都是旋转,并且因此是正交的。
·如果没有已知任何特性,那么邻接矩阵方法(902页的方程A.38),克拉默法则,LU分解,或者高斯消元可以被用于计算逆矩阵(见A.3.1节)。克拉默法则和邻接矩阵总体上是更好的,因为他们有较少的分支操作;在现代架构中避免“if”测试是好的。见4.1.7节中如何使用邻接矩阵求逆去变换法线。
在优化时,可以将计算逆矩阵的目的也考虑上。例如,如果逆矩阵将被用于变换向量时,通常仅矩阵左上3×3部分需要被求逆(见前面章节)。
4.2 特殊矩阵以及其操作
在这一节,一些与实时计算机图形学息息相关的矩阵的变换和操作将被介绍和推导。首先我们展示欧拉变换(以及它的参数的提取),一个描述朝向的直观方法。然后我们涉及从一个单独矩阵返回一系列基础的图形变换。最后,一个让实体绕任意轴旋转的方法被推导出来。
4.2.1 欧拉变换
这个图形变换是一个直观的方法,去构建一个矩阵,以确定你自己(也就是说摄像机)或者其他实体在某个方向的朝向。它的名字来自伟大的瑞士数学家莱昂哈特·欧拉(1707-1783)。
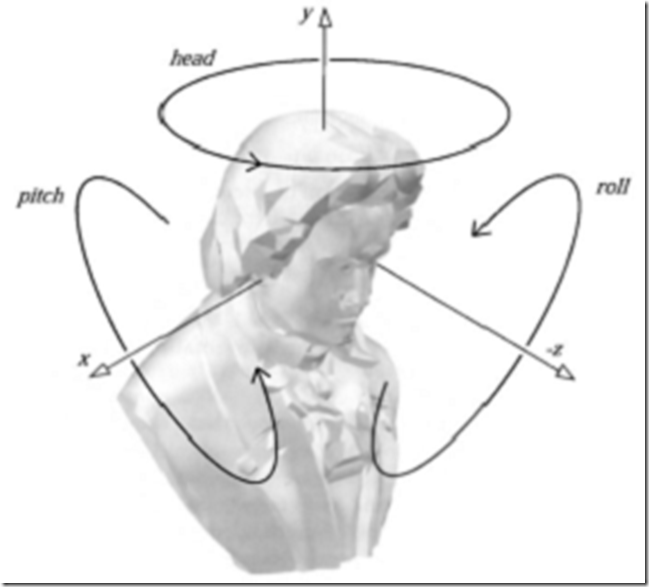
图4.6 以欧拉变换的术语描述,你转动你的head, pitch和roll。默认的视图方向被展示,朝z轴负向看而且head朝向沿着y轴。
某种默认的视觉方向必须首先被建立。通常它会沿z轴负向且head朝向沿y轴,就像图4.6所示的那样。欧拉变换是三个的矩阵的相乘,即图中所示的旋转。更确切地说,这个以E标记的转换矩阵,以方程4.17给出:
E(h, p, r)=Rz(r)Rx(p)Ry(h) (4.17)
因为E是一个旋转矩阵的串接。它无疑也是正交的。因此它的逆矩阵可以表达为E-1=ET=(RzRxRy)T=RyTRxTRzT,尽管当然是更容易使用的E的转置矩阵直接。
欧拉角h,p和r代表顺序和head,pitch和roll应该绕他们对应的轴转过多少度。这变换是直观的并且因此易于与外行人讨论。例如,改变head角度使得观察者摇晃他的头说不,改变pitch使得他点头,而roll使他的头侧倾。注意到的是这个图形变换不仅可以给摄像机定向,也可以用于其他对象或实体。这些变换可以用于世界空间的全局坐标轴或者相对一个局部框架的参考。
当你使用欧拉变换,一种叫做万向锁的情况可能出现。发生这种情况是,旋转使得物体失去一个自由度。例如,变换的顺序是x、y、z。考虑一个绕y轴转π/2的转动,第二个旋转运行。实施这样的旋转后局部坐标的z轴将会与原来坐标的x轴重合,如此的话最后绕z的旋转成了冗余的。
另一个看到失去一个自由度的方法是设置p=π/2并检查欧拉矩阵E(h, p, r)发生了什么:
因为矩阵是依赖于一个角(r+h),我们断定失去了一个自由度。
欧拉角一般按x、y、z的顺序出现在模型系统中,然而绕局部坐标的旋转也可以按照其他顺序的。例如,用于动画的z、x、y和用于动画和物理的y、x、z。所有都是合法的指定三个分离旋转的方式。最后一个顺序,y、x、z,对于某些应用场景是表现优秀的,因为只有当绕x轴转过π弧度(转一半)才会引发万向锁。这就是说,“毛球定理”万向锁是不可避免的,没有完美的顺序可以避免它。
虽然对于小角度的改变和观察者定位十分有用,欧拉角有其他很严重的限制。将两个欧拉角组合起来是很困难的。例如,一个欧拉角与另一个之间的插值不是简单地对每个角进行插值。事实上,两个不同的欧拉角可以得出相同的朝向,所以任何插值都不应该旋转对象。这些是使用另外的一些朝向表达,例如后面讨论的四元数,的原因。
4.2.2 从欧拉变换中提取参数
在某些情况,能够从正交矩阵中提取欧拉参数h,p和r是很有用的。这个提取步骤如方程4.19所示:
串接这方程4.19产生的三个旋转矩阵
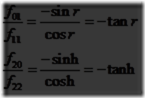
从这可以明显地看到参数pitch由sinp=f21给出。同样的,f01除以f11,以及相似的f20除以f22,推导出了接下来用于参数head和roll的提取公式:
因此,欧拉参数h(head),p(pitch),r(roll)使用函数atan2(y, x)(见第一章中的第7页)从矩阵F中提取如公式4.22所示:
但是,这里有一个特殊例子我们需要处理。当cosp=0时它发生,因为这时f01=f11=0,而因此函数atan2不能使用。Cosp=0意味着sinp=±1,所以F可以简化为
剩余的参数可以通过任意设置h=0,那么sinr/cosr=tanr=f10/f00,通过r=atan2(f10, f00)得到。
注意到arcsin(见B.1节)的定义域为[-π/2, π/2],这意味着如果F如果由这个范围以外的值p创建,那么就不能提取原来的参数。h,p和r不是唯一的,多于一组的欧拉角参数可以产生同样的变换。更多欧拉角的转换可以在Shoemake的1994的论文中看到。以上描述的简单的方法会产生数值不稳定的问题,这在损失一定速度后可以避免。
例子:图形变换的限制。想象你正拿着一个靠在螺栓上的扳手并绕x轴旋转扳手以上紧螺栓。现在假设你的输入设备(鼠标,数据手套,轨迹球等)给出扳手运动的正交变换。你遇到的问题是你并不愿意将变换应用在这个一般应该只绕x轴旋转的扳手上。因此为了将输入的变换P,限制在绕x轴的旋转,使用本节介绍的方法提取欧拉角h,p和r并且创建新的矩阵Rx(p)。这是一个很好用的能使扳手绕x轴旋转的变换(如果P包含了这样的运动)。
4.2.3 矩阵分解
到现时为止,所有的工作都基于假设我们知道所用的变换矩阵的变化的源头和历史。这并不是常见的情况:例如,除了与变换对象相关的已串接矩阵外没有其他东西。从串接矩阵中返回多个矩阵的任务叫做矩阵分解。
需要返回一系列变换的原因有很多,包括:
·为对象提取缩放因子。
·查找粒子系统所需的图形变换。例如,VRML使用变换节点(见4.1.5节)并且不允许使用任意的4×4矩阵。
·检测模型的变换是否只含有刚体图形变换。
·当仅可以获得对象的矩阵时,可以在关键帧之间进行动画插值。
·将剪切变换从旋转矩阵中移除。
我们已经展示了两种分解,这些包括在一个刚体变换中划分平移和旋转矩阵(见4.1.6节),以及在一个正交矩阵中划分出欧拉角(见4.2.2节)。
像我们看到的,返回整个平移矩阵并不是重要的,因为我们只需要这个4×4矩阵的最后一行。我们也可以通过检查矩阵的行列式是否为负从而确定反射是否发生。为了区分旋转,缩放和剪切需要更多工作。
幸运的是在网上可以获取到相当多的关于这方面的论文,以及代码。Thomas和Goldman都提出了稍微不同的对应各种类型变换的方法。Shoemake对用于仿射矩阵的技术进行改进,他的算法独立于参照物的框架并试图分解矩阵以得到刚体变换。
4.2.1 绕任意轴的旋转
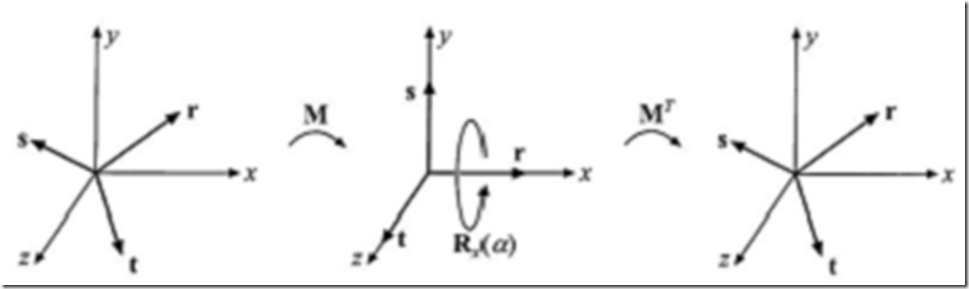
某些时候如果能够让一个实体绕任意轴转动一定角度是十分方便的。假设旋转轴r是标准化的而且变换被创建为绕r旋转α弧度。
为此,首先找到任意两个单位长度的,与r都两两相互正交,也就是标准正交的轴。由这些形成一个空间的基。其方法就是将空间的基从标准空间的基转变为这个新的基,然后绕x轴(与r轴相对应)旋转α个弧度,并且最后变换回标准空间基。这个过程在图4.7展示。
图4.7 绕任意轴r的选择是通过找到由r,s和t组成的标准正交的基完成的。接下来将这个基与标准基对齐,使得r与x轴对齐。绕x轴的选择在此执行,然后变换回去。
第一步是计算基的标准正交的轴。第一个轴是r,也就是旋转所绕的那一个。我们现在集中到寻找第二个轴s,而第三个轴t将会是第一个轴和第二个轴的叉乘,t=r×s。一个数值稳定的实现方法是找到r的最小分量(绝对值)并将它设置为0。交换另外两个分量,然后将这些数字的第一个取负。数学上可以表示为:
这保证了![]() 是正交(垂直)于r,而(r,s,t)是一个标准正交的基。我们可以如下将这三个向量作为矩阵的行:
是正交(垂直)于r,而(r,s,t)是一个标准正交的基。我们可以如下将这三个向量作为矩阵的行:
这个矩阵将r变换到x轴(ex),s变换到y轴和t变换到z轴。所以绕标准化向量r旋转α个弧度最终的矩阵为
X=MTRx(α)M (4.26)
简而言之,这意味着我们先变换已使得r成为x轴(使用M),接着我们绕x轴旋转α个弧度(使用Rx(α)),接着我们使用M的逆矩阵变换回来,在这个例子中是MT,因为M是正交的。
Goldman展示了另一个绕任意轴r旋转φ个弧度的方法。我们在这简单展示他的变换:
在4.3.2节,我们展示了解决这种问题的另一种方法,使用四元数。这也是这章中处理相关问题,例如从一个向量旋转到另一个向量的更高效的算法。
4.3 四元数
尽管四元数可以追溯到1843年Sir William Rowan Hamilton关于复数的扩展,它直到1985年才被Shoemake引入到计算机图形学科中。四元数是一个功能强大的工具,在构造图形变换有着引人注目的特性,在某些方面,它超越了欧拉角与矩阵,尤其是对于旋转和定向。给出坐标轴和角度的代表,变换或计算一个四元数是很直观的。然而欧拉角在任意一个角度的变换都是困难的。四元数可以用于稳定不变的朝向插值,欧拉角在这方面变现不好。
一个复数包含了实数和虚数。两者都由实数字代表,第二个实数乘以![]() 。相似地四元数有四个部分。前三个数值与旋转的轴紧密相关,旋转的角度影响所有四部分(关于这些的更多在4.3.2节)。每个四元数由4个与不同部分关联的实数代表。因为四元数有四个部分,我们使用向量去代表它,但为了区分它们,我们给它们戴个帽子:
。相似地四元数有四个部分。前三个数值与旋转的轴紧密相关,旋转的角度影响所有四部分(关于这些的更多在4.3.2节)。每个四元数由4个与不同部分关联的实数代表。因为四元数有四个部分,我们使用向量去代表它,但为了区分它们,我们给它们戴个帽子:![]() 。我们由一些四元数的数学背景开始,这些将用于四元数的构建和有用的变换。
。我们由一些四元数的数学背景开始,这些将用于四元数的构建和有用的变换。
4.3.1数学背景
我们从四元素的定义开始。
定义 四元数q可被下列方法定义,这些方法都是等效的
变量qw被称为四元数![]() 的实数部分,虚数部分是qv,而i,j和k叫做虚单元
的实数部分,虚数部分是qv,而i,j和k叫做虚单元
对于虚部,,我们使用正常的向量运算,例如加减数乘,点乘,叉乘及更多其它。根据四元数的定义,两个四元数![]() 和
和![]() 相乘推导如下。注意到虚单元的乘法是不满足交换律的。
相乘推导如下。注意到虚单元的乘法是不满足交换律的。
乘法:
如方程所示,我们对两个四元数的相乘使用了叉乘和点乘。由四无数的定义可得出其加法,共轭,标准化和单位四元数如下:
当![]() 被简化(结果展示如上),其虚部被消除而只有实数部分保留。标准化有时可标记为
被简化(结果展示如上),其虚部被消除而只有实数部分保留。标准化有时可标记为![]() 。上述的结果是乘法逆元,标房为
。上述的结果是乘法逆元,标房为![]() ,这可被推导。方程式
,这可被推导。方程式![]() 必须成立(因为这是乘法逆元共有的)。我们取模的定义推导出公式
必须成立(因为这是乘法逆元共有的)。我们取模的定义推导出公式
这给出乘法逆元如下:
逆元的公式使用了标量乘法,这个运算源自公式4.29的乘法:![]() ,而
,而![]() ,这意味着标量乘法是可交换的:
,这意味着标量乘法是可交换的:![]()
以下一系列的定理可以容易从定义中获是:
乘法法则:
对于一些三维向量uq,例如||uq||=1,因为
这些且仅当uq.uq=1=||uq||2才成立。像在下一节所见,单位四元数是十分适合构建高效旋转和朝向。但在此之前,一些对于单位四元数的额外运算将被引入。
对于单位四元数的对数及幂运算如方程4.38:
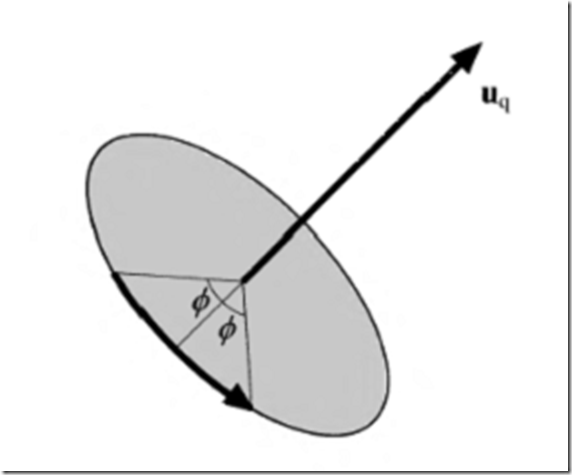
图4.8 由单位四元数![]() 代表的旋转变换的图例。变换绕uq轴旋转2φ个弧度。
代表的旋转变换的图例。变换绕uq轴旋转2φ个弧度。
4.3.2 四元数图形变换
我们现在研究四元数的一个子类,即其长度为单位长,称为单位四元数。单位四元数的重要之处在于它们可代表任意三维旋转,并且其表示是极为简洁和简单。
现在我们描述什么使单位四元素对于旋转和朝向如引有用。首先,将点或向量的四个坐标(Px Py Pz Pw)T放入四元数![]() 的分量,并假定我们有一个单位四元数
的分量,并假定我们有一个单位四元数![]() 。那么
。那么
旋转![]() (并由此点P)绕轴uq转2φ弧度。注意到因为
(并由此点P)绕轴uq转2φ弧度。注意到因为![]() 是一个单位四元数,
是一个单位四元数,![]() 。这个旋转在图4.8上展示出来,它显然可被用于绕任意轴旋转。
。这个旋转在图4.8上展示出来,它显然可被用于绕任意轴旋转。
任何![]() 的非零实数乘法也代表相同的变换,这意味着
的非零实数乘法也代表相同的变换,这意味着![]() 和-
和-![]() 代表相同的旋转。这就是对uq取负轴,和实数部分,qw,创建一个像原来的四元数那样旋转和四元数。这也意味着由矩阵中提取四元数可以返回
代表相同的旋转。这就是对uq取负轴,和实数部分,qw,创建一个像原来的四元数那样旋转和四元数。这也意味着由矩阵中提取四元数可以返回![]() 和-
和-![]() 。
。
给出两个单位四元数,![]() 和
和![]() ,串联连结是先后将
,串联连结是先后将![]() 和
和![]() 应用到一个四元数,
应用到一个四元数,![]() (可认为是点P),由公式4.41给出:
(可认为是点P),由公式4.41给出:
矩阵转换
因为某些系统将矩阵乘法用硬件实现,而且事实上矩阵乘法相较公式4.40有更高的效率,我们需要一个矩阵与四元数的相互转换的方法。四元数,![]() ,可以被转换成矩阵Mq,像公式4.42所表达的:
,可以被转换成矩阵Mq,像公式4.42所表达的:
一旦四元数被构建,就不再需要计算三解函数了,因此在实践中,这转换过程是高效的。
相反的转换,从正交矩阵,Mq,转换到一个单位四元数,![]() ,泛及更多方面。这过程的关健是下面由方程4.43中的矩阵的不同之处:
,泛及更多方面。这过程的关健是下面由方程4.43中的矩阵的不同之处:
这组公式暗示如果qw是已知,向量vq可似被算出,而因些![]() 可被导出,Mq的迹(见898页)可以被计算为
可被导出,Mq的迹(见898页)可以被计算为
这个结果对单位四元数产生以下的变换:
为了在数值上能稳定,应避免除以一个小值数。因此,首先设![]() 由此可得
由此可得
这意味着最大的m00,m11,m22以及u决定了qx,qy,qz和qw那个最大,如果qw是最大,那么公式4.46被用于导出四元数。否则,我们注意到下面:
在方程4.44用于计算![]() 剩余的部分之后,以上之一的合适方程用于计算qx,qy和qz之间的最大值。幸运的是在这一章最后的进一步阅读和资源中有这方面的代码。
剩余的部分之后,以上之一的合适方程用于计算qx,qy和qz之间的最大值。幸运的是在这一章最后的进一步阅读和资源中有这方面的代码。
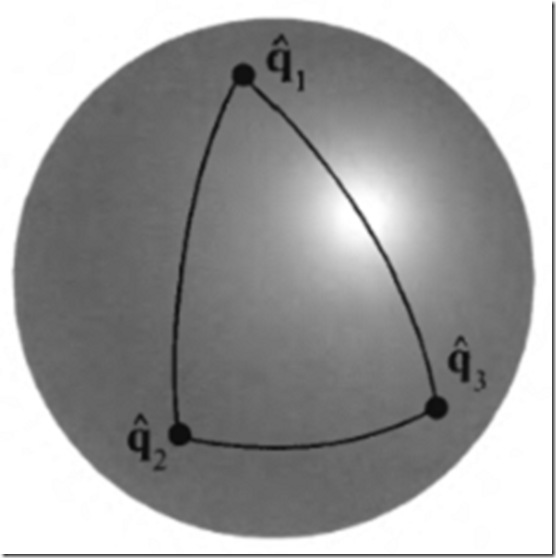
球面线性插值
球面线性插值是一个这样的运算,给出两个单位四元数,![]() 和
和![]() ,以及参数t∈[0,1],计算之间的插值四元数。这对动画对象很有用。它在摄像机朝向的插值用处不大,因为摄像机的“上”向量会在插值中变倾斜,这通常是不好的效果。
,以及参数t∈[0,1],计算之间的插值四元数。这对动画对象很有用。它在摄像机朝向的插值用处不大,因为摄像机的“上”向量会在插值中变倾斜,这通常是不好的效果。
但是,对于软件实现,以下的形式,球形线性插值点,是更为合适:
为了计算φ这一方程所需的值,以下可用:![]() ,对于t∈[0,1],球面插值函数计算一系列(唯一的)插值四元数一起组成了四维单位球上由
,对于t∈[0,1],球面插值函数计算一系列(唯一的)插值四元数一起组成了四维单位球上由![]() (t=0)到
(t=0)到![]() (t=1)的最短弧。圆弧落在
(t=1)的最短弧。圆弧落在![]() 、
、![]() 以及原点所给出的平面与四维单位球体相交所形成的圆形上。这如图4.9所示。计算的旋转四元数绕固定轴似恒定速度旋转。这样的以常速运行,因此加速为零的曲线,叫做测地曲线。
以及原点所给出的平面与四维单位球体相交所形成的圆形上。这如图4.9所示。计算的旋转四元数绕固定轴似恒定速度旋转。这样的以常速运行,因此加速为零的曲线,叫做测地曲线。
图4.9 单位四元数用于表示单位圆上的点。Slerp函数用于四元数间的插值,并且插值路径是球上的弧,注意到由![]() 到
到![]() 的插值与由
的插值与由![]() 到
到![]() 再到
再到![]() 的插值不是同一样,即使他们最后都到达同一朝向。
的插值不是同一样,即使他们最后都到达同一朝向。
Slerp函数十分适合在两个朝向间的插值并且它表现得很好(固定轴,常速)。在使用一些欧拉角进行插值时并非如此。在实践中,直接计算slerp是一个昂贵的运算,涉及了三角函数的调用。Li提供了更快的递增方式去计算Slerps并用不牺牲精度。
当多于两个朝向,记为![]() ,可得,而我们希望从
,可得,而我们希望从![]() 到
到![]() 再到
再到![]() ,直到
,直到![]() 进行插值,Slerp可直接使用。现在当我们接近
进行插值,Slerp可直接使用。现在当我们接近![]() ,我们会以
,我们会以![]() 和
和![]() 为Slerp插值的参数。之后越过
为Slerp插值的参数。之后越过![]() ,我们会使用
,我们会使用![]() 和
和![]() 作为Slerp的参数。这会使朝向插值出现突然间的急速变化,这可见于图4.9。与之相似的是点被线性插值,见578页图13.2的右上部分。一些读者可能想在读完13章关于样条曲线后重读接下来的段落。
作为Slerp的参数。这会使朝向插值出现突然间的急速变化,这可见于图4.9。与之相似的是点被线性插值,见578页图13.2的右上部分。一些读者可能想在读完13章关于样条曲线后重读接下来的段落。
一个更好的插值方法是使用某种样条曲线。我们在![]() 和
和![]() 之间引入四元数
之间引入四元数![]() 和
和![]() 。球面立方插可被定义一系列四元数,
。球面立方插可被定义一系列四元数,![]() ,
,![]() ,
,![]() 和
和![]() 中。出乎意料地,三个额外的四元数可如下被计算:
中。出乎意料地,三个额外的四元数可如下被计算:
![]() 和
和![]() 会用于四元数的球面插值,使用三次样条平滑,如方程4.52:
会用于四元数的球面插值,使用三次样条平滑,如方程4.52:
由上可见,squad函数通过重复球面插值使用slerp构建(见13.1.1节中关于点的重复线性插值的信息)。插值会经过初始朝向![]() ,i∈[0,...,1],缺不穿过
,i∈[0,...,1],缺不穿过![]() ——这是用于指示初始朝向的切线朝向。
——这是用于指示初始朝向的切线朝向。
从一个向量旋转到另一个
通常的操作是从一个方向s通过最短路径转到t。四元数数学极大地简化了这一步骤,并且展示了四元数与这一表示方式的紧密关系。首先,规范化s和t ,然后计算单位旋转轴,称为u,通过![]() 计算,下一步,
计算,下一步,![]() 并有
并有![]() ,这2φ是s和t之间的夹角。四元数表示由s旋转到t是
,这2φ是s和t之间的夹角。四元数表示由s旋转到t是![]() ,实际上使用半角关系(见19页)以及三角函数恒等式(公式B.9)可将
,实际上使用半角关系(见19页)以及三角函数恒等式(公式B.9)可将![]() 简化为
简化为
以这种方式直接生成四元数(相较于规范化s与t 的叉乘)避免了当s与指向几乎相同的t叉乘时数值上的不稳定。稳定性问题同样出现在s和t指向相反方向,因为出现了除以零。当检测到这样的特殊例子,任何垂直于s的转动轴可用于旋转至t。
有时我们需要矩阵表示从s到t 的旋转。在代数和三角函数简化公式4.43后,旋转矩阵变为
在这个方程,我们使用以下的中间计算:
就像可见的,所有平方根和三角函数由于化简而消失,因此这是一个高效的构建矩阵的方法
需特别注意到,当s与t 是平行或都几乎平行,因此||s×t||≈0。如果φ≈0那么我们可似返回单元矩阵。然而,如果2φ≈π,那么我们可似绕任何轴旋转π个弧度。这个轴可以由s和其它任意不平行于s的向量的叉积而得(见4.24节)。Moller和Hughes使用户主矩阵以不同的方式处理这种特殊的情况。
例子:为摄像机设置位置和朝向。假设默认的虚摄像机(或视点)的位置是(0 0 0)T并且默认的视觉方向v是沿z轴负向,也就是说是v=(0 0 -1)T。现在,目标是创建一个变换将摄像机移到新的位置p,看向新的方向w。由摄像机的定向开始,这可以由从默认视图方向转到目标视图方向实现。R(v,w)负责这些。定位是简单地由平移到p实现,这产生了结果变换X=T(p)R(v,w)。在实践中,在第一次旋转之后其它的向量与向量间的旋转很可能会将视图向上方向旋转到所需要的方向。
4.4顶点混合
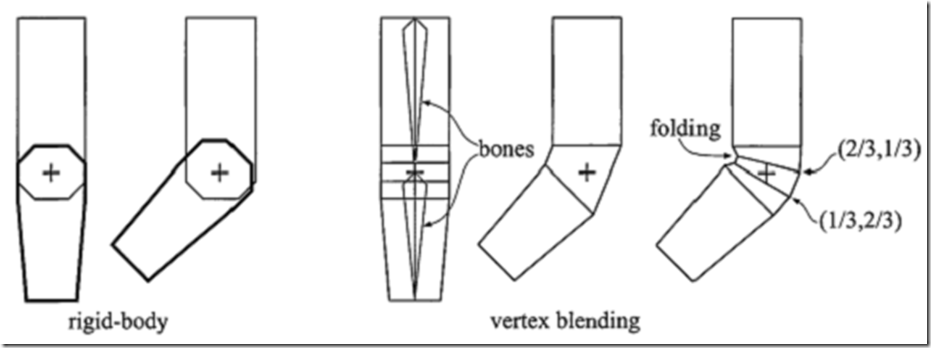
设想一个数字人物的手臂动画化被分为两部分,前臂和上臂,像图4.10左边那样显示。这个模型的动画可使用刚体变换(见4.1.6节)。但两部分间的连接点却不像真正的手肘。这是因为使用的是两个分离的对像,而且因此连接点由两个分离的对像的重合部分组成。显然,使用一个独立的对象更好。然而,静态模型部分并不能使连接点灵活。
图4.10 一个手臂由前臂和上臂组成,其动画化使用左边的两个分离对象的刚体变换。手肘并未表现真实。对于右边,顶点混合用于一个单独的对象。最右边旁边的手臂展示了当一个简单的皮肤直接连接两部分覆盖手肘将会发生什么。最右边手臂展示了当顶点混合被使用将会发生什么,并且一些顶点被以不同的权重进行混合:(2/3, 1/3)意味着顶点的变换的权重是上臂2/3,前臂1/3。这图也在最右边展示了顶点混合的不足,这里,在手肘内部的折叠是可见的,更好的结果可以由更多骨骼,以及更细的权值设定而获得。
顶点混合是这个问题的一个解决方案。这技术有许多其它名称,例如蒙皮,包络和骨骼子空间变形。虽然这所展示的算法的精确起源不为人所清楚,但定义骨骼并使皮肤对变化作出反应是计算机动画的旧概念。在它最简单的形式,前臂及上臂像此前那样,但在连接点,两个部件通过弹性的“表皮”连接。因此,这个弹性部分将会有一组顶点由前臂矩阵变换,而另一组由上臂矩阵变换。这个结果为三角形,其顶点可能被不同的矩阵变换,与每个三角形都使用单独的矩阵形成鲜明的对比。见图4.10。这种基本的技术叫做拼接。
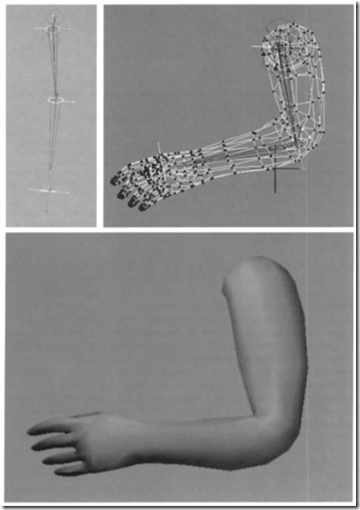
在这步继续深入,一个单独的顶点可以被多个不同矩阵变换,并包含了结果位置的加权混合。这由拥有骨骼的动画对象实现,其每个骨骼的变换会通过用户自定义的权重影响每一各顶点。因为整个手臂可能都是“有弹性的”,也就是,所有的顶点可以被一个以上的矩阵影响,整个网格通常称为皮肤(包裹着骨骼)。见图4.11。很多商业建模系统拥有这同种骨骼建模的功能。虽然有这样一个名称,但骨骼并非一定需要是刚硬的。例如,Mohr和Gleicher提出了关于增加额外的连接点以启用例如肌肉膨胀的效果的想法。James和Twigg讨论了动画蒙皮使用可以压缩和拉伸的骨骼。
图4.11 一个真实的顶点混合例子。左上图片在一个延伸的位置上展示手臂的两个骨骼。右上图展示了网格,并且以颜色标记了每根骨骼所拥有的顶点。下面的图:着色后的手臂网格,与前图位置稍异。
这在数学上被表示为公式4.56,其p是顶点原本位置,而u(t)是变换后顶点,其位置由时间参数t确定。n块骨骼影响着p的位置(即其世界坐标)。矩阵Mi从原来的骨骼坐标系统变换到世界坐标系。典型的是骨骼有它在其坐标系统原点的控制节点。例如,前臂骨骼会以手肘节点为原点,以动画旋转矩阵绕着该节点移动手臂的这部分。Bi(t)矩阵是第i块骨骼随时间变化使对象动画化的世界变换,并且通常是一些列矩阵的串联,例如层次化中之前的骨骼变换以及局部动画矩阵。Woodland深入讨论了一个维护和更新Bi(t)矩阵动画功能的方法。最后,wi是骨骼i对定点p的权重。定点混合公式是
每块骨骼都就自有的框架参考点变换顶点,而最终的位置是由一些列计算出来的点插值得出的。在蒙皮的一些讨论中,矩阵Mi不是显式展示的,而是被当做Bi(t)的一部分。我们在这展示它是因为它是有用的矩阵,几乎总是矩阵串接过程的一部分。
在实践中,每帧动画的每块骨骼的矩阵Bi(t)和Mi-1串接一起,而且每个结果矩阵都是用于变换顶点的。顶点p被不同骨骼串接后的矩阵变换,并且使用权重wi混合到一起——因此名为顶点混合。权重为非负数值以及其和为1,因此顶点根据一些位置变换并在其中插值的情况将会发生。同样地,变换后的点u会位于一些列点Bi(t)Mi-1p(固定时刻t下由0到n-1的所有的i)。法向量通常也可以由公式4.56变换。根据变换的使用(例如如果一块骨骼被延伸或者压缩一个相当大的数值),Bi(t)Mi-1的逆矩阵可以由转置矩阵代替,就像4.1.7节中讨论的那样。
顶点混合十分适合用于GPU。网格中的一系列顶点可以至于静态缓存中,一次性提交给GPU然后重复使用。在每一帧中只有骨骼矩阵发生变化,顶点着色器计算他们在已存储的网格上产生的作用。在这个方法中,数据处理和与CPU交互的数据量是最少的,允许GPU高效地渲染网格。如果模型的整套骨骼可以一起使用的话是最容易的;否则模型就必须分割并且一些骨骼将会重复。
使用顶点着色器时,可以指定[0,1]以外,或者总和不为1的一组权重。但是,这样使得场景只能使用其他的混合算法,例如目标变形(见4.5节)正被使用。
原始的顶点混合的一个缺点是会发生不需要的折叠、扭曲和自相交。见图4.12。一个最佳的解决方法是使用Kavan以及其他人所展示的对偶四元数。这个处理蒙皮的技术帮助保留原变换的刚性,故避免了肢体发生“糖果包裹纸”般的扭曲。计算量小于线性蒙皮混合的1.5倍,并且结果优秀,导致该技术的快速普及。感兴趣的读者可以参考该论文,它也包括了一关于之前关于线性混合改进的简述。
图4.12 左边的图展示了使用线性混合时在连接点发生的问题。在右边,使用对偶四元数的混合改进了其外观。
4.5 变形
在展示动画时,从一个三维模型变形到另一个是十分有用的。一个模型的图像在时刻t0显示而我们希望它在时刻t1变换到另一个模型。对于t0到t1之间的所有时间,由某种差值得出一个连续的“混合”模型。图4.13展示了一个变形的例子。
图4.13 顶点变形。两个位置和法线定义了每个顶点。每一帧中,中间位置和法线被顶点着色器线性差值得出。
变形由两个主要的问题构成,分别是顶点对应问题和插值问题。给出两个任意的模型,它们有着不同拓扑结构、不同顶点和不同的网格连接,首先通常需要从设置这些顶点的对应关系开始。这是一个困难的问题,而且这方面已有很多的研究。感兴趣的读者可以参考Alexa的综述[16]。
然而,如果两个模型间顶点的一对一对应,那么插值可以在逐顶点的基础上实现。这就是,对于第一个模型的每个顶点,在第二个模型中必须存在唯一一个对应的顶点,反之亦然。这使得插值成了简单的任务。例如,线性插值可以直接应用到顶点中(见13.1节中其他插值的方法)。为了计算时间在[t0,t1]之间的变形顶点,我们首先计算s=(t-t0)/(t1-t0),而线性顶点混合为
m=(1-s)p0+sp1 (4.57)
其中p0和p1 对应同一顶点在不同时刻t0和t1 。
一个有趣的变形的变体被称作为目标变形或者形状混合[671],它使得用户能够更为直观地控制。其基本的理念可由图4.14解析。
图4.14 给出两个嘴巴的姿势,一组不同的向量被计算出来去控制内插插值,或甚至外推插值。在目标变形,不同顶点的向量被用于向中性的面部“增加”动作。随不同的向量的位置权重,我们得出了一个微笑的嘴巴,而负值的权重可以给出相反的效果。
我们从一个中性的模型开始,在这个例子中是一张脸。我们标记这个模型为N。此外,我们也有一组不同的面部表情。在例子中仅有一个微笑的表情。通常,我们可以允许标记为Pi,i∈[1,...,k]的不同表情的k≥1。作为前处理,“表情的差异”被计算为:Di=Pi-N,也就是每个表情模型中减去中性表情。
在这一点,我们有中性模型,N,以及一组姿势差异,Di。一个变形后的模型M可以使用一下公式得到:
这是中性模型,而紧接着我们按需要使用权重wi增加不同的姿势。对于图4.14,设置w1=1给出了图中间的精确的笑脸。使用 w1=0.5给出半笑的表情,等等。也可以使用负向或者大于1的权重。
对于这个简单的面部模型,我们可以以增加另外的拥有忧伤眉毛的脸。因为位移是可附加的,这个眉毛的位置可以结合微笑嘴巴的姿势使用。目标变形是一个强大的技术为动画制作人提供更多的控制,因为模型的不同突出部可以独立与其他部分而被操控。Lweis等人[770]介绍了骨骼(姿势)空间变形,它结合了顶点混合和目标变形。硬件支持的DirectX 10可以使用流输出和其他改进的功能实现在单个模型上使用多个目标并且仅在GPU中计算效果[793]。
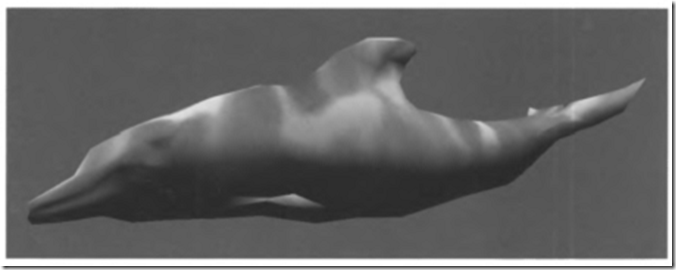
图4.15展示了一个使用蒙皮和变形的真实例子。
图4.15 瑞秋角色面部表情和动作由蒙皮和顶点变形控制,它在使用图形硬件支持下可以加速
4.6 投影
在渲染一个场景之前,所有在场景中相关的对象必须投影在某个平面上或者投影到某个简单形体中。此后再执行裁剪和渲染(见2.3节)。
这章中迄今为止所见的变换都留下第四个分量,w,不作改变。也就是说点和向量在变换后仍保留着他们的类型。同样的是4×4矩阵的最底一行总是(0 0 0 1)。透视投影矩阵对这些属性而言是个例外:底行包含向量和点的操纵数字,而且通常需要齐次化过程(也就是w通常不是1,因此需要除以w去获得非齐次点)。这节中先前处理的正交投影,是一种简单的被普遍应用的投影。它不会影响w分量。
在这一节中,假设视角是朝z轴的负向看,y轴朝上而x轴朝右。这是右手坐标系。一些文章和软件,例如DirectX,使用的是左手坐标系,其视角是朝z轴正。两者都是同样正确的,并且能达到同样的效果。
4.6.1 正交投影
一个正交投影的特征是在投影后平行线依然是平行线。下面所示的矩阵Po是一个简单的正交投影矩阵,它留下点的x和y分量不变,而设置z分量为0,也就是它正交地投影到z=0的平面上:
这个投影的效果展示在图4.16。明显的,Po是不可逆,因为它的行列式|Po|=0。简而言之,变换从三维降到二维,而且没有办法重新获得所丢弃的那一维。使用这种正交投影成像存在一个问题,那就是它将z分量正值和负值的点都投影到一个投影平面上。它能将z值(或者x,y值)限制在某一个区间,形成所说的从n(近平面)到f(远平面)。这是下一个变换的目的。
图4.16 公式4.59生成的简单正交投影的三个不同的视角。这投影可以认为视角是沿着z轴负向,这意味着投影简单地略过坐标z(或者设置为0),但保留x和y坐标。注意到z=0的两边都被投影到投影面上。
一个更为普遍的执行正交投影的矩阵以一个六个数组合的方式表述,(l,r,b,t,n,f),标记为左、右、下、上、近、远平面。这个矩阵本质上是轴对齐(AABB;定义见16.2节)地缩放和平移,由这些平面形成一个轴对齐的以原点为中心的立方体。AABB的最小转角是(l,b,n)而最大转角是(r,t,f)。认识到n>f很重要,因为我们是在空间是沿着z轴负向去看。我们的常识是近的数值应该小于远的。同样是朝z轴负向看的OpenGL,在调用glOrtho生成正交投影矩阵时以小于远值的近值作为输入参数,而后在内部将两个参数取负。另一种方法是认为OpenGL的近值和远值是沿视角方向(负向z轴)的(正的)距离,而非z视点坐标值。
OpenGL的轴对齐立方体有最小转角(-1,-1,-1)以及最大转角(1,1,1);DirectX的范围则是(-1,-1,0)到(1,1,1)。这个立方体叫做正规化可视空间而这个空间的坐标叫做规范化设备坐标。图4.17展示了变换的过程。转换到正规化可视空间的原因是在这个状态下裁剪更为高效。
图4.17 在正规化视图空间中变换轴对齐。在左边的盒子是第一个变换,使得它的中心位于原点。之后它像右边所示的,缩小至正规化视图空间。
在变换到正规化视图空间后,将被渲染的几何体的顶点会被这个立方体裁剪。不在立方体外的几何体最终通过将剩余的单位正方形映射到屏幕而被渲染。OpenGL中这个正交投影如下:
正如公式所示,Po可被写成变换的串接,T(t),接着是缩放矩阵,S(s),其中s=(2/(r-l), 2/(t-b), 2/(f-n)),而t=(-(r+l)/2, -(t+b)/2, -(f+n)/2)。这个矩阵是可逆的,也就是说Po-1=T(t)S((r-l)/2, (t-b)/2, (f-n)/2)。
在计算机图形学中,投影后通常使用左手坐标系——也就是说,对于视口,x轴指向右,y轴指向上,而z轴指向里。因为我们定义轴对齐包围盒(AABB)的方式是远值小于近值,所以正交投影变换通常包含一个镜像变换。要明白这个,所谓轴对齐包围盒大小保持不变是规范化视图空间的目标。于是,轴对齐包围盒的坐标是(-1, -1, -1)对应(l, b, n)而(1, 1, -1)对应(r, t, f)。公式4.60推导出:
这是一个镜像矩阵。这个镜像将右手坐标系(朝z轴负向看)转换为左手的规范化的设备坐标系。
DirectX将z深度映射到范围[0, 1]而OpenGL则是[-1, 1]。这可以在应用正交投影矩阵后通过应用简单的缩放和平移矩阵而实现,这就是,
因此,DirectX使用的正交投影矩阵为
这通常以转置的形式出现,因为DirectX使用行主元去输出矩阵。
4.6.2 透视投影
一个相较正交投影更为有趣的投影是透视投影,它被应用于大多数的计算机图形程序。此时,投影后平行线一般不再平行,他们会在极远处汇聚成一个点。透视投影更为接近我们对真实世界感知,简而言之,远处的物体通常更小。
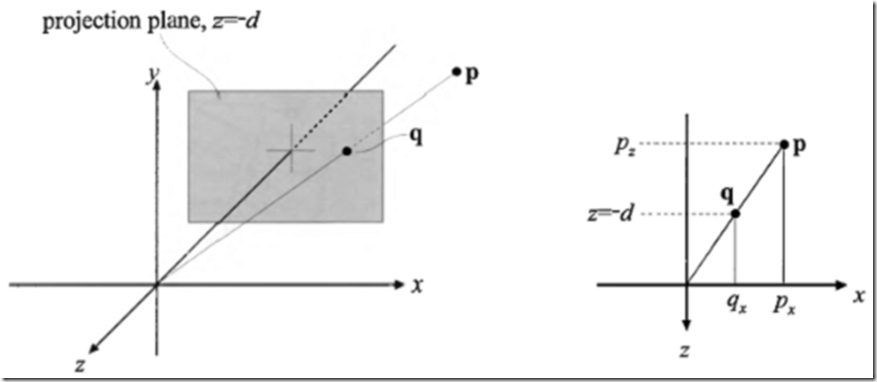
首先,我们展示一个启发性的透视投影矩阵的推导,这个投影投影到z = -d的平面,d > 0。我们从世界空间开始推导,简化关于世界到视图转换的理解。这个推导之后就是更为常用的矩阵使用,例如OpenGL。
图4.18 用于导出透视投影矩阵的图标。点p被投影到z = -d平面(d > 0),产出投影点q。投影由位处原点的透视摄像机产生。推导时使用的x分量的相似三角形如右图所示。
假设摄像机(视点)被放置在原点,而我们希望投影一个点,p,到z = -d的平面(d > 0)而产生一个新的点q(qx, qy, -d)。这个场景如图4.18所描述。从这幅图所示的相似三角形,以下关于q的x分量的推导可得:
q的另一个分量的表达式为qy=-dpy/pz(推导与qx相似),并且qz=-d。联合上面的公式,我们得出投影透视矩阵,Pp,如下:
这个矩阵是否产生正确的透视投影可简单地通过公式4.66验证:
最后一步是整个向量都除以w分量(例子中的-pz/d),使得w分量保持为1。Z值的结果总是为-d,因为我们投影到一个平面。
直觉上容易理解为何齐次坐标允许投影。一几何的解释是齐次化的过程是将点(px,py,pz)投影到w=1的平面。
对于正交变换,也是一个透视变换,不是实际投影到一个平面上(这是不可逆的),而是将视图平截头体变换到前面所说的标准视图空间。这里的视图平截头体设定为始于z = n而终于z = f,其中0 > n > f。在z=n的正方形有小角(l, b, n)而最大角在(r, t, n)。这展示在图4.19中。
图4.19 矩阵Pp将视图平截头体变换到单元立方体(也就是所谓的规范化可视空间)
参数(l, r, b, t, n, f)决定了摄像机的视图平截头体。视体的水平视野由平截头体的左右平面(由l和r确定)间的夹角决定。水平视野越大,摄像机看到的就越多。非对称平截头体通过r≠-l或t≠-b创建。非对称平截头体用于诸如立体感的观察(见18.1.4节)和CAVEs[210]。
视体的视野是一个给出场景真实感觉的重要因素。相比计算机屏幕,视点本身有一个物理实体上的视野,其关系为:
Φ=2arctan(w/(2d)) (4.67)
其中φ是视野,w是对象垂直于视线的宽度,而d是对象的距离。例如,一个21英寸监视器是大约16英寸宽,而最小的推荐观看距离(产生35度的实体视野)是25英寸。当距离为12英寸,视野是67度;18英寸,则为48度;30英寸,则为30度。这个简单的公式可以用于将摄像机镜头转换到视野,例如,一个标准的50mm镜头对于35mm摄像机(拥有36mm外框尺寸)给出Φ=2arctan(36/(2*50))=39.6度。
使用一个相比实体更窄的视野设置会降低透视的效果,就像观察者在场景中被放大。设置一个更宽的视野会使得对象表现得出现扭曲(像使用广角镜),尤其是在靠近屏幕的边缘会增大旁边对象的比例。但是,更宽的视野使得观察者感觉场景更为广大和震撼,并有提供用户更多周遭信息的好处。
将平截头体变换到单元立方体的透视变换矩阵由公式4.68给出:
在对点应用变换后,我们得到另一个点q=(qx,qy,qz,qw)T。这个点的W分量,qw,既非零也不等于1。为了得到投影的点,p,我们需要除以qw:p=(qx/qw,qy/qw,qz/qw,1)T。矩阵Pp总是实现z=f对应+1而z=n对应-1。透视投影被执行,裁剪和齐次化(除以w)会被执行以得到规范化的设备坐标。
为了得到OpenGL的透视变换,因为与正交投影相同的原因首先乘以s(1,1,-1)。这可以简单地通过对公式4.68的第三列数值取负实现。在这镜像变换被应用后,其远值和近值会变成正值,其中0< n’< f’,就像它传统展示给用户那样。然而,它依然代表沿着世界坐标系的z轴负向,这个视图的方向。为了提供参照,这是OpenGL的公式:17
一些APIs(例如DirectX)将近平面对应为z = 0(而非z = -1)而远平面z = 1。还有,DirectX使用左手坐标系定义它的投影矩阵。这意味着DirectX沿z轴正向看,并且近值和远值都为正数。以下是DirectX的公式:
DirectX在它的文档中使用行主元的形式,所以这个矩阵通常以转置的形式出现。
使用透视变换的一个效果是深度计算值并非与输入的pz值成线性变化。例如,如果n’= 10和f’= 110(使用OpenGL的术语),当pz是60个单位沿z轴负向(也就是中间点)规范化设备坐标深度值为0.833,而非0。图4.20展示了不同的近平面到原点距离的影响。近远平面的放置影响着Z缓存的精度。这个影响将在18.1.2节中深入讨论。
图4.20 不同近平面与原点距离的影响。距离n’- f’恒定保持为100。当近平面靠近原点,远平面附近的点使用一个较小的规范化设备坐标深度空间。这个影响使得当点距离近平面远时z缓存降低精度
进一步阅读和资源
一本以较不痛苦的方式建立一个人对矩阵的直觉的书是Farin和Hansford的《The Geometry Toolbox》[333]。另一本有用的著作是Lengyel的《Mathematics for 3D Game Programming and Computer Graphics》[761]。对于不同的视角,很多计算机图形学文章,例如Hearn和Baker[516],Shirley[1172],Watt和Watt[1330],和Foley等人的两本书[348,349],都包括了矩阵的基本知识。《Graphics Gems》系列[36,405,522,667,982]展示各种变换相关的算法并在线提供相应的代码。Golub和Van Loan的《Matrix Computations》[419]是综合研究矩阵技术的一个起点。见http://www.realtimerendering.com中用于不同变换的代码,包括四元数。更多的关于骨骼子空间的变形、顶点混合和形体插值可以阅读Lewis等人的SIGGRAPH论文[770]。
Hart等人[507]和Hanson[498]提供了一个可视化的四元数。Pletinckx[1019]和Schlag[1126]展示在一系列的四元数见进行平滑插值的不同方法。Vlachos和Isidoro[1305]堆到了用于四元数C2插值的公式。与四元数插值问题相关的是沿曲线计算一个一致的坐标系统。这为Dougan[276]尝试。
Alexa[16]和Lazarus和Verroust[743]展示了关于不同变形技术的综述。