|
很多球友,对直接有下球线路的球,已经练习到成功率过70%了。但是切磋中经常会遇见被做安全球之后。束手无策,盲目解球。造成给对手自由球的机会。丢掉好好的局势。 今天。我特别查了资料,给大家附上颗星公式,希望对你有用。 一、母球撞一岸解球。 这是解障碍球最常用的方法。由于具体情况千变万化,我们很难靠几个范例来总结,但万变不离其宗基本原理就是在理想状态下,母球撞案的反射角等于入射角。现实中由于球案的弹性,母球的旋转,击球力度的变化,反射角通常是不等于入射角的。但是在击球的力度很柔,而且母球不带有任何侧旋(不加塞)的情况下,反射角与入射角的偏差就非常小,可以忽略。这个原理是撞案救球的基础,但在事实上同样的入射角,击球的力量越大,反射角就越大;加塞的情况就更复杂,要靠反复的练习去慢慢体会了。 应用公式解球首先要了解两个概念,一是星点数值的定义,就是给花式九球台边的刻度赋值。这个公式星点数值的定义为球杆延伸至岸边的星点数值为0;二是母球旋转值,即我们说的加塞,数值越大塞加得越大,击球点在范例中均已标明。 范例一:如图,球杆延伸至球台的点为0,目标点为6,所以第1岸星点应该是2的位置。 算法为6=2(第1岸星点)x2+2(母球旋转值) 需要说明的是,所谓第1岸星点的瞄准点,并不是母球撞岸点正好在2,而是瞄准2的点打,实际撞点应该靠前一些,后面的例子均如此。母球旋转值2即图中所示击球点,为右塞(顺塞)。
 范例二:如图,球杆延伸至球台的点为0,目标点为8,所以第1岸星点应该是3的位置。 8=3(第1岸星点)x2+2(母球旋转值)。 范例二:如图,球杆延伸至球台的点为0,目标点为8,所以第1岸星点应该是3的位置。 8=3(第1岸星点)x2+2(母球旋转值)。 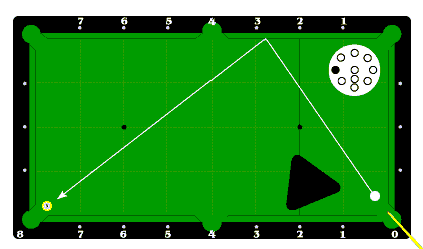 范例三:球杆延伸至球台的点为0,目标点为6,所以第1岸星点应该是2的位置。 6=2(第1岸星点)x2+2(母球旋转值)。如图 范例三:球杆延伸至球台的点为0,目标点为6,所以第1岸星点应该是2的位置。 6=2(第1岸星点)x2+2(母球旋转值)。如图 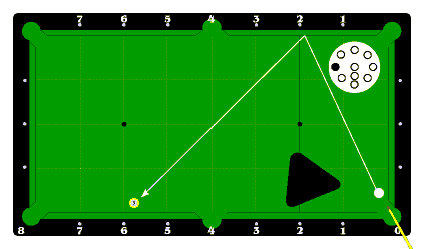 此打法需要加强烈的顺塞,比较难以掌握,这里仅供参考。我个人觉得也未必科学,比如这几个例子都是撞长边的,如果撞短边呢,母球旋转值为2就显然多了。吃一库解球的应用最多,一定要灵活掌握,感觉很重要,所以平时要多加练习。 此打法需要加强烈的顺塞,比较难以掌握,这里仅供参考。我个人觉得也未必科学,比如这几个例子都是撞长边的,如果撞短边呢,母球旋转值为2就显然多了。吃一库解球的应用最多,一定要灵活掌握,感觉很重要,所以平时要多加练习。 |
很多球友,对直接有下球线路的球,已经练习到成功率过70%了。但是切磋中经常会遇见被做安全球之后。束手无策,盲目解球。造成给对手自由球的机会。丢掉好好的局势。
今天。我特别查了资料,给大家附上颗星公式,希望对你有用。
一、母球撞一岸解球。
这是解障碍球最常用的方法。由于具体情况千变万化,我们很难靠几个范例来总结,但万变不离其宗基本原理就是在理想状态下,母球撞案的反射角等于入射角。现实中由于球案的弹性,母球的旋转,击球力度的变化,反射角通常是不等于入射角的。但是在击球的力度很柔,而且母球不带有任何侧旋(不加塞)的情况下,反射角与入射角的偏差就非常小,可以忽略。这个原理是撞案救球的基础,但在事实上同样的入射角,击球的力量越大,反射角就越大;加塞的情况就更复杂,要靠反复的练习去慢慢体会了。
应用公式解球首先要了解两个概念,一是星点数值的定义,就是给花式九球台边的刻度赋值。这个公式星点数值的定义为球杆延伸至岸边的星点数值为0;二是母球旋转值,即我们说的加塞,数值越大塞加得越大,击球点在范例中均已标明。
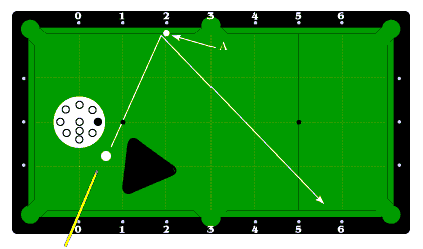
范例一:如图,球杆延伸至球台的点为0,目标点为6,所以第1岸星点应该是2的位置。
算法为6=2(第1岸星点)x2+2(母球旋转值)
需要说明的是,所谓第1岸星点的瞄准点,并不是母球撞岸点正好在2,而是瞄准2的点打,实际撞点应该靠前一些,后面的例子均如此。母球旋转值2即图中所示击球点,为右塞(顺塞)。

范例二:如图,球杆延伸至球台的点为0,目标点为8,所以第1岸星点应该是3的位置。
8=3(第1岸星点)x2+2(母球旋转值)。

范例三:球杆延伸至球台的点为0,目标点为6,所以第1岸星点应该是2的位置。
6=2(第1岸星点)x2+2(母球旋转值)。如图

此打法需要加强烈的顺塞,比较难以掌握,这里仅供参考。我个人觉得也未必科学,比如这几个例子都是撞长边的,如果撞短边呢,母球旋转值为2就显然多了。吃一库解球的应用最多,一定要灵活掌握,感觉很重要,所以平时要多加练习。
今天。我特别查了资料,给大家附上颗星公式,希望对你有用。
一、母球撞一岸解球。
这是解障碍球最常用的方法。由于具体情况千变万化,我们很难靠几个范例来总结,但万变不离其宗基本原理就是在理想状态下,母球撞案的反射角等于入射角。现实中由于球案的弹性,母球的旋转,击球力度的变化,反射角通常是不等于入射角的。但是在击球的力度很柔,而且母球不带有任何侧旋(不加塞)的情况下,反射角与入射角的偏差就非常小,可以忽略。这个原理是撞案救球的基础,但在事实上同样的入射角,击球的力量越大,反射角就越大;加塞的情况就更复杂,要靠反复的练习去慢慢体会了。
应用公式解球首先要了解两个概念,一是星点数值的定义,就是给花式九球台边的刻度赋值。这个公式星点数值的定义为球杆延伸至岸边的星点数值为0;二是母球旋转值,即我们说的加塞,数值越大塞加得越大,击球点在范例中均已标明。
范例一:如图,球杆延伸至球台的点为0,目标点为6,所以第1岸星点应该是2的位置。
算法为6=2(第1岸星点)x2+2(母球旋转值)
需要说明的是,所谓第1岸星点的瞄准点,并不是母球撞岸点正好在2,而是瞄准2的点打,实际撞点应该靠前一些,后面的例子均如此。母球旋转值2即图中所示击球点,为右塞(顺塞)。

范例二:如图,球杆延伸至球台的点为0,目标点为8,所以第1岸星点应该是3的位置。
8=3(第1岸星点)x2+2(母球旋转值)。

范例三:球杆延伸至球台的点为0,目标点为6,所以第1岸星点应该是2的位置。
6=2(第1岸星点)x2+2(母球旋转值)。如图

此打法需要加强烈的顺塞,比较难以掌握,这里仅供参考。我个人觉得也未必科学,比如这几个例子都是撞长边的,如果撞短边呢,母球旋转值为2就显然多了。吃一库解球的应用最多,一定要灵活掌握,感觉很重要,所以平时要多加练习。