任务:实现一个能够生成数独局并且能求解数独问题的控制台程序。
1、GitHub:https://github.com/MiaoZhou48/SoftwareEngineeringProject
2、时间耗费
|
PSD2.1 |
Personnal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
| Planning | 计划 | 40 | 40 |
| .Estimate | .估计这个任务需要多长时间 | ||
| Development | 开发 | 150 | 120 |
| .Analysis | .需求分析(包括学习新技术) | 180 | 200 |
| .Design Spec | .生成设计文档 | 150 | 150 |
| .Design Review | .设计复审(和同事审核设计文档) | 60 | 60 |
| .Coding Standard | .代码规范(为目前的开发制定合适的规范) | 60 | 60 |
| .Design | 具体设计 | 80 | 80 |
| .Coding | .具体编码 | 1600 | 1800 |
| .Code Review | .代码复审 | 100 | 150 |
| .Test | .测试(自我测试,修改代码,提交修改) | 200 | 250 |
| Reporting | 报告 | 120 | 150 |
| .Test Report | .测试报告 | 80 | 100 |
| .Size Measurement | .计算工作量 | 40 | 30 |
| .Postmortem & Process Improvement Plan | .事后总结,并提出过程改进计划 | 50 | 40 |
| 合计 | 2910 | 3190 |
3、解题思路:
此项目可以细分为两个功能:生成数独、解数独。
生成数独我考虑采用的是回溯的方法,对残缺数独不断求解,从而得到相应数量的完善的数独。
确定好方法之后便是漫长的学习之路,参考了相应的回溯算法的博客以及其他算法的数独生成博客。
在学习过程中也见识到了很多新的思路生成数独,比如说对一个已经合理的数独进行变换,然后判断其在变换之后是否依然是符合数独规范。通过这种方式生成数独,首先会保证结果的互异性,其次相比于回溯不需要大量的计算,节省了大量的时间。
但是由于已经开始用回溯算法写了,所以之后的改进阶段会再尝试一下敢变思路。
4、设计实现过程
程序主体是3个函数
judge():解数独函数中用此函数判断回溯条件。
solve():具体的解函数本体。
construct():构建函数。
封装成函数有利于代码的复用,与此同时提升了程序的简洁性和可读性。
函数逻辑说明:
生成数独函数construct():首先进入函数判断目前生成的数独是否数量达标,若符合标准则结束函数体,否则进入下一步。下一步判断一下1-9个数字是否经过遍历数字全排列完,若是则跳到行间的全排列判断,若行全排完就结束函数体,否则改变行的排列顺序再初始化数排列进行终局输出。若判断数字全排未完,就改变数字的顺序再进行终局生成。也就是两个嵌套的判断,数字全排和行数组的全排。
解数独函数solve():解数独首先加一个判断条件,看是否已经生成了需求规定的9x9数独,若是输出数独并结束;否则进行递归:利用judge函数判断防止条件,能放就放并进入下一层递归,不能就回溯到上一层遍历到下一个数再进行递归,最终递归结束返回最初的判断,进行数独输出。
其实思路很简单但是实际运行的话,若给定的数独数量是1000000或更大跑的时间差不多是在20s,所以还是有待提升的。
5、性能改进及思路
测试程序的时候,同学建议我优化一下数字的输出,construct函数其实是最耗时的,所以优化也是从这里着手。
之前使用的printf输出格式,但其实putchar()这种以字符形式输出会更节省时间,所以我替换了之前的printf输出方式,结果生成时间减少到了7s左右,相较之前的20多秒提升了很多。
性能测试:
这是输入为1000000时的性能情况
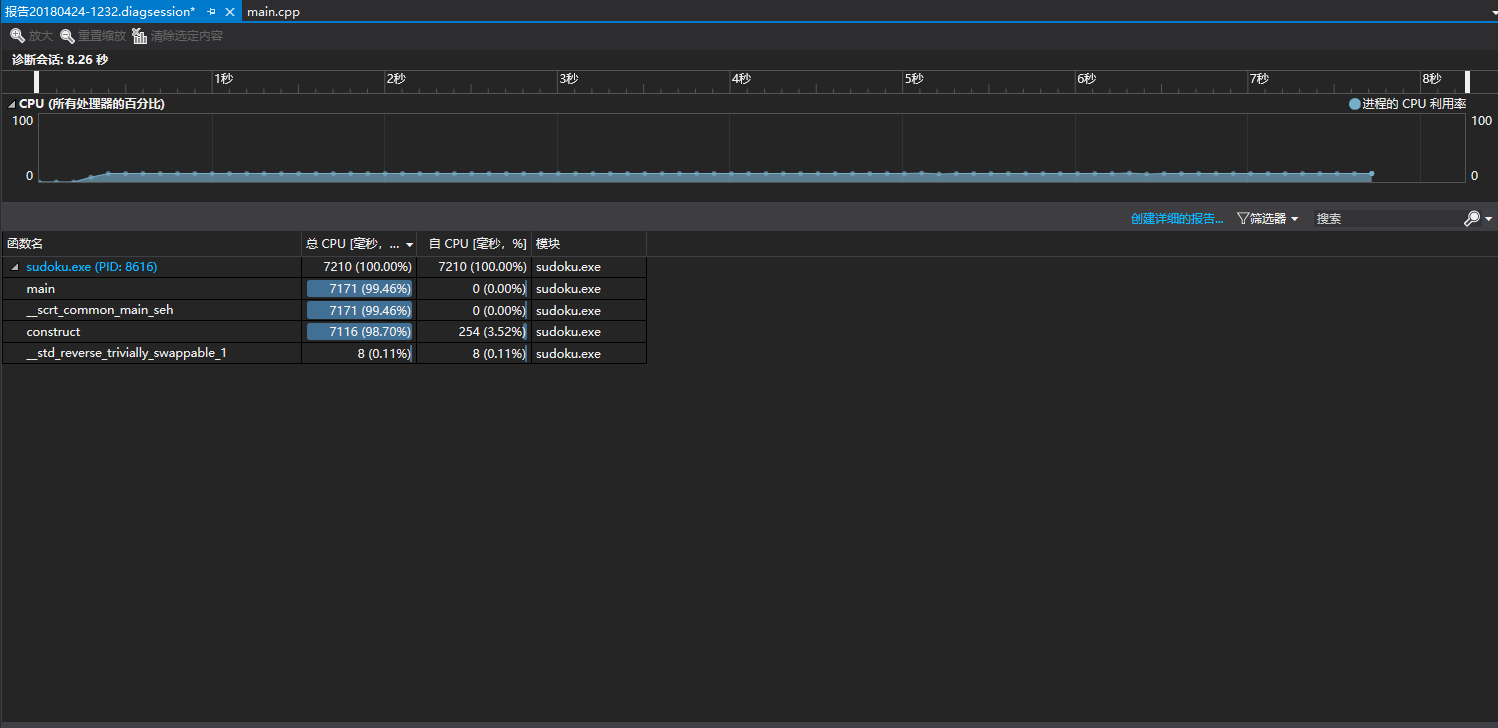
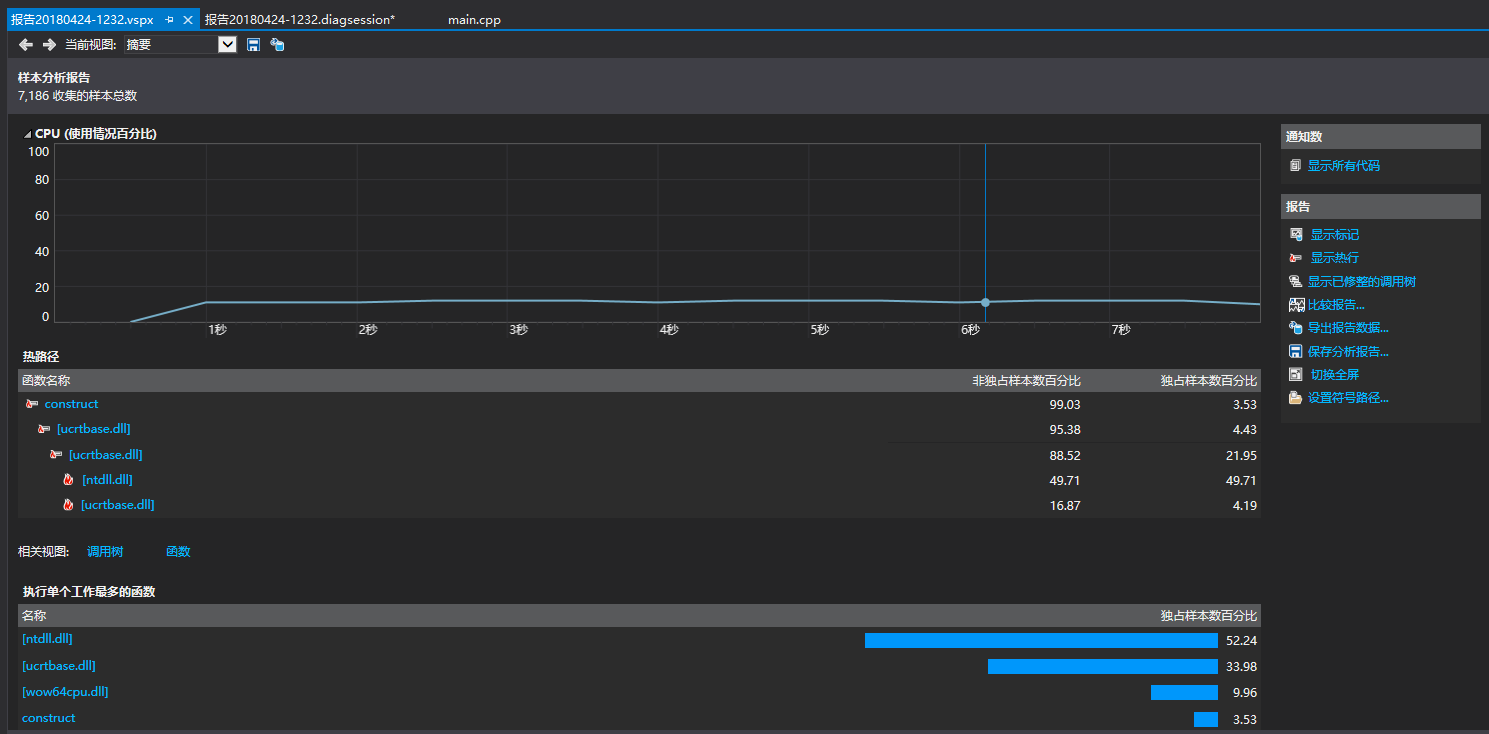
6、代码说明(思路解释+注释说明)
旁边的小铭同学提供给我一种非常好的思路:就是对任意的一个终局数独,任意交换1-3、4-6、7-9行的顺序得到的依然是满足需求的数独,这也就弥补了8!=40320远远小于1000000这样的大数字的尴尬境地。
下面是具体的construct()函数代码

void construct(int n) { int count = 0; int trans[10] = { 0, 0, 6, 5, 4, 3, 2, 1, 7, 8 }; int Temp_column; char fn[10] = { '9','7','1','2','3','4','5','6','8','9' }; if (count < n) { for (int a = 0; a < 6; a++) { if (count == n) break; if (a) next_permutation(trans + 4, trans + 6); for (int b = 0; b < 6; b++) { if (b) next_permutation(trans + 7, trans + 9); int t = 0; char kong = ' '; do{ if (t) next_permutation(fn + 2, fn + 9); for (int i = 1; i <= 9; i++) { for (int j = 1; j <= 9; j++) { if (j - trans[i] >= 0) Temp_column = j - trans[i]; else Temp_column = j - trans[i] + 9; putchar(fn[Temp_column % 9]); if (j < 9) printf(" "); } printf(" "); } count++; t++; if (count == n) break; else printf(" "); } while (t<40320); if (count == n) break; } } } }
下面是具体的solve()函数代码

void solve()//解数独 { judge(1, 1); int flag = 0,countcolumn[10] = { 0 }; for (int i = 1; i <= 9; i++) { int counts[10] = { 0 }; for (int j = 1; j <= 9; j++) { if (!Tdarray[i][j]) { flag = 1; break; } else { if (j == 1) countcolumn[Tdarray[i][j]]++; counts[Tdarray[i][j]]++; if (counts[Tdarray[i][j]] > 1 || countcolumn[Tdarray[i][j]] > 1) { flag = 1; break; } } } if (flag) { cout << "解数独失败" << ""; break; } } if (!flag) { for (int i = 1; i <= 9; i++) { for (int j = 1; j <= 9; j++) { putchar(Tdarray[i][j]); if (j < 9) putchar(' '); } if (i < 9) putchar(' '); } } }
解数独就是要有一个判断函数judge()用来在遍历的阶段看是否能够发放置这个数,思路就是回溯法~
7、实际耗时
具体的时间消耗见最上方的表格。
