-
正交
正交对于向量来说是内积/点积为0,对于函数来说是乘积的积分为0. -
共轭
对于复数来说是实部相同,虚部相反。
对于函数来说,共轭对称函数是实部为偶函数,而虚部为奇函数的函数。 -
周期函数可以表示为离散傅里叶级数(三角级数)加权和。
-
非周期函数可以看成一个周期无限大的函数,在一个周期内同样可以分解为不同频率的函数之和,如果频率分量是连续的,那么求和就变成了积分。
而不同频率的函数,用复平面上一个旋转的点来表示,为了消除虚部的分量,我们把积分下限扩展到了 -无穷。我们得到的频率分量前面的权值,就是频谱函数的y坐标。 -
傅里叶级数和Fourier Transform的统一。
一个周期实函数(还要满足一些其他条件)可以表示为带系数的正交三角函数(或者用欧拉公式表示三角函数,这样也会引入虚数部分,但是虚数部分正负相互抵消了)之和,而系数部分是一个复数形式的。当写成系数*e的幂级数时,与傅里叶变换的幂级数幂次符号正好相反。因此可以理解为,对于能做FT的函数,它的FT是求系数。系数的实部分代表了频率的Amplitude,表达为y轴坐标, 而虚数部分代表相位,x轴代表频率。 -
傅里叶变换之后为什么会有负频率?
我们所看到的频谱其实是对应频率的magnitude,或者说对应F(w)=R(x)+jI(x)=O(x)+jE(x)=|F(w)|e^(jwt)的magnitude,|F(w)|。
R(x)代表实函数,I代表imagine function,O代表odd function,E则是even function。
首先,我们是为了把正弦和余弦函数统一表示才引入了e^(x)。
因为实函数的FT结果中,实部是偶而虚部是奇,因此当我们把它和原函数对应,做逆傅里叶变换时偶函数积分相当于正频率积分2,而积分的表达式中可以看出,表达虚数的部分都是奇函数,都变成了0(注意,此处并不是说FT的结果中的I(x)IFT之后没了,因为IFT是乘上e^(jwt)用欧拉展开后发现一部分是虚,另一部分变成了实),结果就又变成一个纯实函数。
并且|F(w)|是一个偶函数。
-
信号的直流分量与信号FT结果中的0频率分量是两个概念,具体见以下链接:
https://dsp.stackexchange.com/questions/21583/difference-between-dc-component-and-zero-frequency-component-of-signal -
离散采样的结果和结果的DFT内含周期性。
因此,离散采样结果f和滤波函数(也是周期函数)l卷积时就会出现warp-around error。而warp-around error的解决方法就是padding,人为拉长两个周期之间的距离。
然而padding也会带来新的问题,当sampled function的边缘非0时,padding之后的结果就会出现一个骤降,这等同于sample function*box function。换句话说,padding之后
的结果做DFT就会出现新的sinc分量,因为我们需要逼近这个骤降,需要无限高频。而这个问题的解决方法就是windowing,padding之后再乘上一个windowing function将这个骤变
平滑处理。 -
频率filter不padding
padding还有一个问题在于,sampled function可以padding,但是filer很难padding,最后DIP的做法是,在频域直接生成和padding之后的sampled function大小一致的filter,
也就是一个padding,一个不做。 -
混叠-整数个周期
有限频率的采样总是会出现频谱混叠,因为现实中的频率总是会有很高频的存在,解决的方法是在采样之前用低通滤波器滤波。
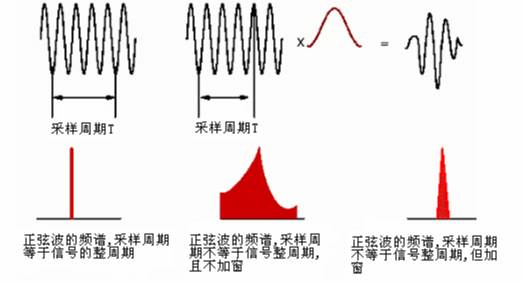
同样的,有限时间的采样很有可能正好把某个频率截断,也就是说图像的边缘很可能分布着大量陡峭的边缘,而这些边缘DFT之后都会产生新的无限高频分量。当我们的截断正好包括了整数个周期,
也就是没有产生任何陡峭的边缘时,就不会产生这种现象,然而这是极少发生的。