树
概念
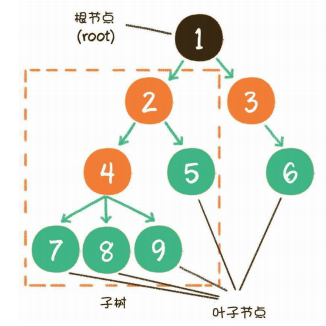
示例

或者企业里的职级关系

又比如一本书的目录
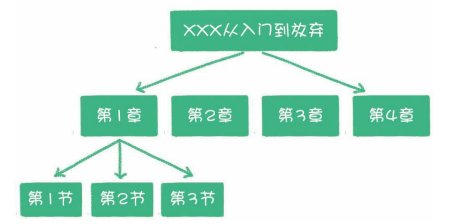
常用树
二叉树
概念

分类
1、满二叉树(完美二叉树)
概念:一个二叉树的所有非叶子节点都存在左右孩子,并且所有叶子节点都在同一层级上,那么这个树就是满二叉树。
图示:

2、完全二叉树
概念:若设二叉树的深度为k,除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大个数,第k 层所有的结点都连续集中在最左边,这就是完全二叉树。
图示:
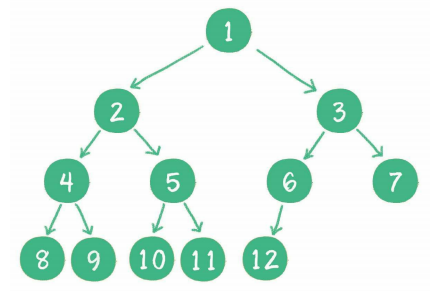
3、平衡二叉树
概念:它或者是一颗空树,或它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1,且它的左子树和右子树都是一颗平衡二叉树。
图示:

二叉树存储
链式存储

- 存储数据的data变量
- 指向左孩子的left指针
- 指向右孩子的right指针
数组存储

二叉树应用
查找
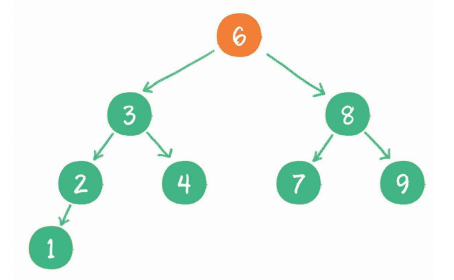
非常适合查找的树-----二叉查找树(Binary Search)
- 如果左子树不为空,则左子树上所有节点的值均小于根节点的值
- 如果右子树不为空,则右子树上所有节点的值均大于根节点的值
- 左、右子树也都是二叉查找树
图示:
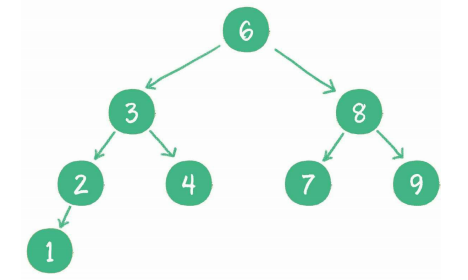
在原本二叉树的基础上增加这些条件又会带来什么样的效果呢?

package arithmetic.com.ty.binary; public class BinarySearchTree { private Node tree; public Node find(int data) { Node p = tree; while (p != null) { if (data < p.data) p = p.left; else if (data > p.data) p = p.right; else return p; } return null; } public static class Node { private int data; private Node left; private Node right; public Node(int data) { this.data = data; } } }
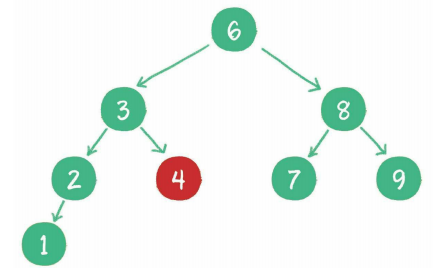
维持相对顺序
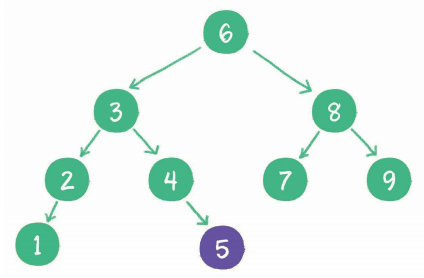
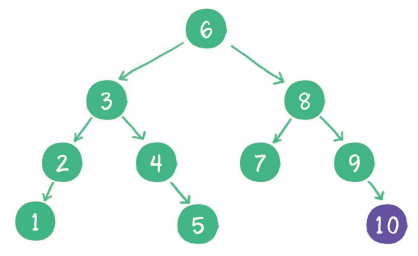
但是二叉查找树也会存在一个问题,例如:
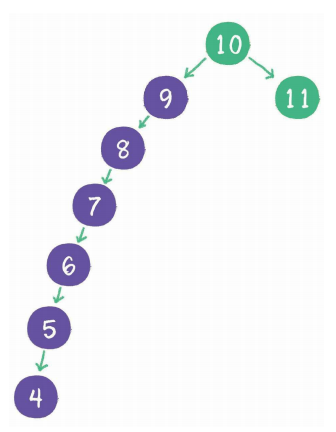
1、插入
public void insert(int data) { if (tree == null) { tree = new Node(data); return; } Node p = tree; while (p != null) { if (data > p.data) { if (p.right == null) { p.right = new Node(data); return; } p = p.right; } else { // data < p.data if (p.left == null) { p.left = new Node(data); return; } p = p.left; } } }
2、删除
针对要删除节点的子节点个数的不同,我们需要分三种情况来处理。
第一种情况是,如果要删除的节点没有子节点,我们只需要直接将父节点中,指向要删除节点的指针置为 null。比如图中的删除节点 55。
第二种情况是,如果要删除的节点只有一个子节点(只有左子节点或者右子节点),我们只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就可以了。比如图中的删除节点 13。
第三种情况是,如果要删除的节点有两个子节点,这就比较复杂了。我们需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 18。

public void delete(int data) { //p指向要删除的节点,初始化指向根节点 Node p = tree; //pp记录的是 p的父节点 Node pp = null; while (p != null && p.data != data) { pp = p; if (data > p.data) { p = p.right; }else { p = p.left; } } if (p == null) { // 没有找到 return; } // 要删除的节点有两个子节点 if (p.left != null && p.right != null) { // 查找右子树中最小节点 Node minP = p.right; Node minPP = p; // minPP 表示 minP 的父节点 while (minP.left != null) { minPP = minP; minP = minP.left; } // 将 minP 的数据替换到 p 中 p.data = minP.data; // 下面就变成了删除 minP 了 p = minP; pp = minPP; } // 删除节点是叶子节点或者仅有一个子节点 Node child; // p 的子节点 if (p.left != null) { child = p.left; }else if (p.right != null) { child = p.right; }else { child = null; } if (pp == null) { // 删除的是根节点 tree = child; }else if (pp.left == p) { pp.left = child; }else { pp.right = child; } }
二叉树遍历
遍历方式
- 前序遍历-----根结点-->左子树-->右子树
- 中序遍历-----左子树-->根结点-->右子树-----中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是 O(n),非常高效。
- 后序遍历-----左子树-->右子树-->根结点
- 层序遍历
- 深度优先遍历(前序遍历、中序遍历、后序遍历)
- 广度优先遍历(层序遍历)
深度优先遍历
概念:所谓深度优先,顾名思义,就是偏向于纵深,“一头扎到底”的访问方式。
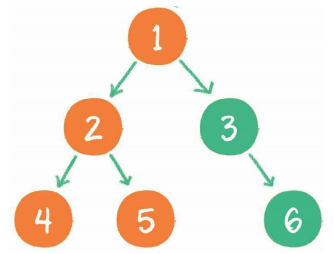
前序遍历
示例:
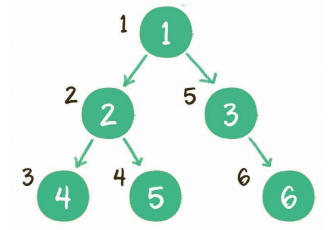
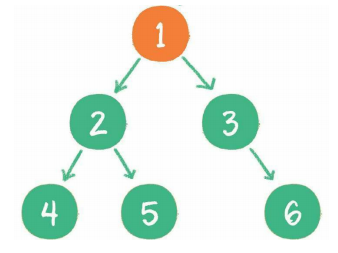
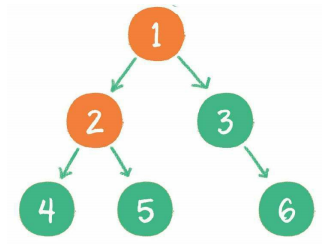




中序遍历




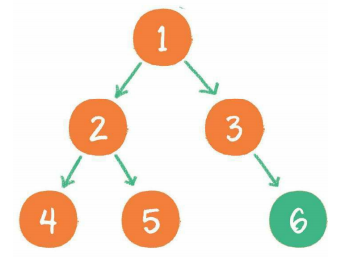

后序遍历
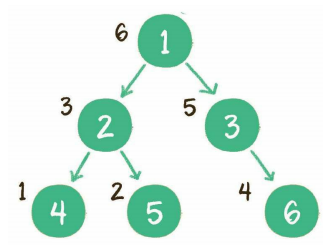
深度优先遍历代码示例:
package arithmetic.com.ty.binary; import java.util.Arrays; import java.util.LinkedList; public class BinaryTreeTraversal { public static void main(String[] args) { LinkedList<Integer> inputList = new LinkedList<Integer>( Arrays.asList(new Integer[] { 3, 2, 9, null, null, 10, null, null, 8, null, 4 })); TreeNode treeNode = createBinaryTree(inputList); System.out.println(" 前序遍历:"); preOrderTraveral(treeNode); System.out.println(" 中序遍历:"); inOrderTraveral(treeNode); System.out.println(" 后序遍历:"); postOrderTraveral(treeNode); } /** * 构建二叉树 * * @param inputList 输入序列 */ public static TreeNode createBinaryTree(LinkedList<Integer> inputList) { TreeNode node = null; if (inputList == null || inputList.isEmpty()) { return null; } Integer data = inputList.removeFirst(); if (data != null) { node = new TreeNode(data); /** * 1、循环LinkedList:{3, 2, 9, null, null, 10, null, null, 8, null, 4} * 2、如果List中不为null是数据,都会封装成TreeNode,并递归创建leftChild * 3、当遇到index为3的null时,创建leftChild=createBinaryTree(inputList)的递归返回,此时leftChild为9 * 4、然后开始执行rightChild = createBinaryTree(inputList),但是index为4的数据依然为null,因此9的兄弟节点为null * 5、然后开始往回执行,此时leftChild为2,开始执行rightChild = createBinaryTree(inputList),因此2的右子树为10 * . * . * . */ node.leftChild = createBinaryTree(inputList); node.rightChild = createBinaryTree(inputList); } return node; } /** * 二叉树前序遍历 * @param node 二叉树节点 */ public static void preOrderTraveral(TreeNode node) { if (node == null) { return; } System.out.println(node.data); /** * 1、leftChild也可能有leftChild以及rightChild,因此需要递归下去 */ preOrderTraveral(node.leftChild); preOrderTraveral(node.rightChild); } /** * 二叉树中序遍历 * @param node 二叉树节点 */ public static void inOrderTraveral(TreeNode node) { if (node == null) { return; } inOrderTraveral(node.leftChild); System.out.println(node.data); inOrderTraveral(node.rightChild); } /** * 二叉树后序遍历 * @param node 二叉树节点 */ public static void postOrderTraveral(TreeNode node) { if (node == null) { return; } postOrderTraveral(node.leftChild); postOrderTraveral(node.rightChild); System.out.println(node.data); } /** * 二叉树节点 */ private static class TreeNode { int data; TreeNode leftChild; TreeNode rightChild; TreeNode(int data) { this.data = data; } } }
广度优先遍历
其基本思想是尽最大程度辐射能够覆盖的节点,并对其进行访问。
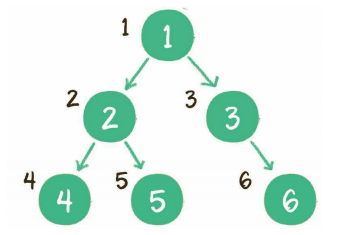
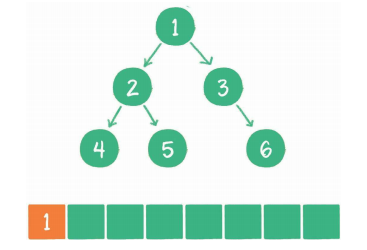


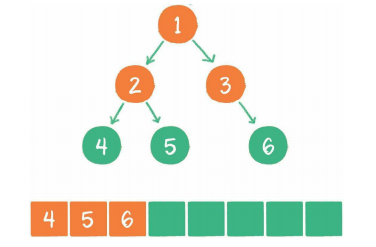
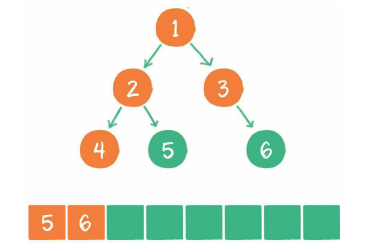
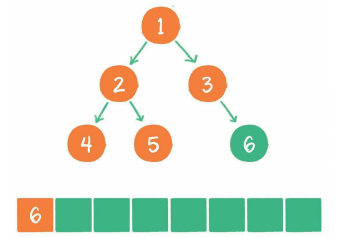

广度优先代码示例:
public static void levelOrderTraversal(TreeNode root) { Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.offer(root); while (!queue.isEmpty()) { TreeNode node = queue.poll(); System.out.println(node.data); if (node.leftChild != null) { queue.offer(node.leftChild); } if (node.rightChild != null) { queue.offer(node.rightChild); } } }