20182307 2019-2020-1 《数据结构与面向对象程序设计》第九周学习总结

20182307 2019-2020-1 《数据结构与面向对象程序设计》第九周学习总结

教材学习内容总结

• 第十六章 树 介绍了另一种数据结构：树。不同于之前学习的栈、队列、链表等线性集合，树是一种非线性集合，其中的元素组织为层次结构。本章还介绍了包括树的分类、四种遍历树的方法在内的知识，完善了树的基本知识的框架。

学习笔记：

• 树
  • 树是非线性结构，其中的元素组织为层次结构
  • 树只有唯一的根结点
  • 树的度表示树中任意结点的最大子结点数
  • 有m个元素的平衡n叉树的高度是logn(m)
• 结点
  • 没有任何子结点的结点称为叶结点
  • 结点的层是从根到该结点的路径长度，而路径长度为从根到该结点的路径上的边数
• 树的遍历
  • 先序遍历：访问根，自左至右遍历子树
  • 中序遍历：遍历左子树，再访问根，然后自左至右遍历剩余子树
  • 后序遍历：自左至右遍历子树，最后访问根
  • 层序遍历：从树顶到树底，从左至右访问每个结点
    • 进行层序遍历时可用队列来存储树中的元素
• 数组计算链
  • 对于存储在数组中位置为n的元素，元素的左子结点存储在(2n+1)的位置，元素的右子结点存储在(2*(n+1))的位置
  • 树的基于数组的存储链实现方式可以占据数组中的连续位置，不管树是不是完全树
• 二叉查找树
  • 对于二叉查找树的每个结点，左子树上的元素小于父结点的值，右子树上的元素大于等于父结点的值
  • 最有效的二叉查找树是平衡的，所以每次比较时可以排除一半的元素
  • 删除元素时需要考虑的三种情况
    • 叶结点
    • 有一个子结点
    • 有两个子结点

教材学习中的问题和解决过程

• 问题1：如何区别先序、中序、后序三种遍历？层序又有何不同？
  • 书本内容：树的遍历有4种基本的方法，这4种方法都从根结点开始
  • 个人理解：先序、中序、后序三种遍历的方法其实从命名方法上就可以读出分辨点，即根据访问根的先后次序来区分。比如，先序遍历就是先访问根，而中序是先访问左子树，中间次序时访问根，最后访问右子树。而层序遍历的思想与前三种无法比较，但却是一种较好理解的遍历方式，即一层层、从左至右的访问各个结点，个人认为是属于最简单的遍历方式。
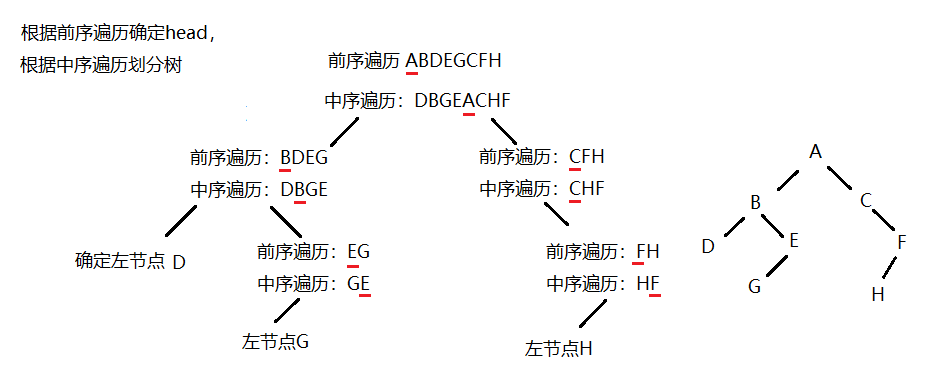
• 问题2：如何根据先序与中序序列构建一棵唯一二叉树
  • 网络资料：根据树前序遍历和中序遍历构建二叉树
  • 个人理解：如果要编写一个这样的程序，首先要注意的是只有已知先序和中序、中序和后序这两种情况的时候才可以确立一棵唯一二叉树，而已知先序和后序是不能确定的，因为左右子树可能不同。所以构建时的基本思想是这样的：先序序列的第一个结点肯定是根节点，所以先在中序序列中找到相同的根节点，以它为划分左右分别为左右子树。再进行相似的步骤，先序序列的第二个元素就是左子树的第一个节点，再在中序序列中以它为中心划分左右子树，以此类推。构建完左边的整个子树后，以相同的原理构建右子树。
    
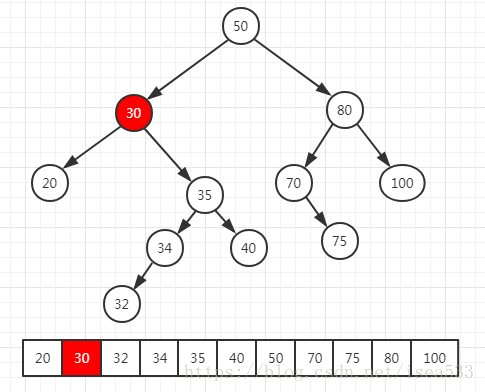
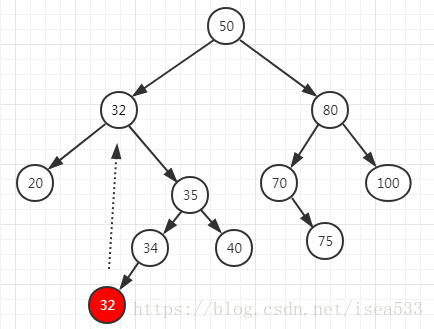
• 问题3：二叉查找树怎么处理三种情况？
  • 书本内容：删除元素时需要考虑的三种情况：叶结点、有一个子结点、有两个子结点
  • 个人理解：首先要清楚删除时的三种情况。最简单的是删除叶子结点的情况，由于叶子结点是没有子结点的，所以不需要考虑重新链接的问题，直接删除即可；若是要删除有一个子结点的结点，只需要用该结点的子结点来替代被删的父结点，程序中使用递归重新链接一次即可；最复杂的是有两个子结点的结点，当遇到这种情况的时候，比较好的解决方法是用被删结点的中序后继结点取代它。所谓中序后继结点即为中序序列中，按顺序出现的下一个结点。实现过程为先从树中删除结点的中序后继，然后用此结点来替代实际要删除的结点。
    
    

代码调试中的问题和解决过程

• 问题1：教材代码中的ArrayIterator类无法识别
  • 原因分析：Iterator模式是用于遍历集合类的标准访问方法。它可以把访问逻辑从不同类型的集合类中抽象出来，从而避免向客户端暴露集合的内部结构.每一种集合类返回的Iterator具体类型可能不同，例如setArray(array)就返回ArrayIterator
  • 
  • 解决方案：修改方法的定义类型为ArrayList
• 问题2：设计决策树的时候，无法按变量命名顺序赋值
  • 原因分析：由于决策树程序所使用的LinkedBinaryTree类中包含的构造方法设计思路是自底向上的，所以要先定义决策树的叶子节点，然后再根据设计逐层向上连接左右子树。所以如果变量赋值不按顺序是正常的。
  • 
  • 解决方案：按照自底向上的顺序定义、赋值变量，最终构建成树

代码托管

上周考试错题总结

• 上周无考试

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	10000行	30篇	400小时
第一周	209/209	2/2	9/9
第二、三周	290/499	2/4	18/28
第四周	516/1015	2/6	22/50
第五周	2981/3996	2/8	32/82
第六周	1498/5494	2/10	20/102
第七周	1519/7013	2/12	51/153
第八周	1641/8654	2/14	21/174
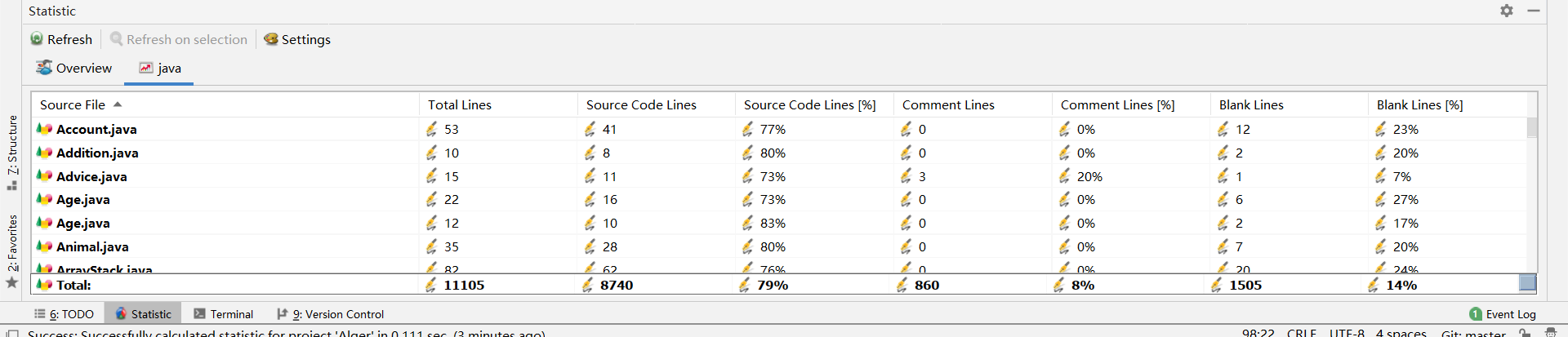
第九周	2451/11105	2/16	30/204

点评过的同学博客和代码

• 本周结对学习情况

  • 20182320
  • 结对照片

• 结对学习内容

  • 树的分类
  • 树的四种遍历方法
  • 二叉树的实现与应用
  • 二叉查找树的实现
  • 决策树的实现

• 上周博客互评情况

  • 20182320