目录:
01. Week01
- 数字通过 #define 来定义,可读性更高,另外就是修改方便
不要忘记 return EXIT_SUCCESS; or return 0;
fiveDigit.c - 计算矩阵內积的时候,其实看上去蛮复杂的
方法:将计算过程写出来,自己找到规律,找到遍历的逻辑
innerProdFun.c
matrixProdFun.c - 可以通过表达式来实现 if 语句
int fastMax(int a, int b, int c) { int d = a * (a >= b) + b * (a < b); // d is max of a and b return c * (c >= d) + d * (c < d); // return max of c and d }fastMax
02. Week02
- 测试系统
int:4 bytes
float:4 bytes
pointer:8 bytes
不足 4 bytes 的补齐
opal.c (注意struct分级构建,重命名之类的)
注意字符串数组保留最后一位
3. The data structure can be improved in various ways:
* encode both origin and destination (''from'' and ''to'') using
Sydney Transport's unique stop IDs along with a lookup table that
links e.g. 203311 to "Anzac Pde Stand D at UNSW"
* use a single integer to encode the possible "Fare Applied" entries
* avoid storing redundant information like the weekday, which can be
derived from the date itself
*/ - fprintf 的下一句,可以是 return 1 or exit(1)
最简单的 Makefile
sumnum: sumnum.c
gcc sumnum.c -o sumnum
clean:
rm -f sumnum
sumnum.c - 递归的思路就是找出递推公式,然后找到第一项的成立条件
类似以前学的递推数列的思路,肯定会给一个关系和前几个值
recount+.c
03. Week03
- atoi() does no error detection: it simply returns 0 if its argument is non-integer.
sum3argB.c - getchar() 一个字符一个字符读取,按照 不等于 EOF 可以判断是否到达文件结尾
scanf() 可以读取一行
如果读取多行的字符串,只需利用while循环即可,知道无法获取合理的字符串为止
char str[10];
while (scanf("%s", str) == 1) {
printf("%s
", str);
}
04. Week04
- 数组的地址运算,不是直接加数字,需要乘以数据类型本身占据的空间(bytes)
int nums[12] = {5,3,6,2,7,4,9,1,8};
and assuming that &nums[0] is 0xbabeface, what are the values of the following expressions?
nums + 4
类似 *(nums + 4) 表示 index 为 4 的元素
所以 nums + 4 == 0xbabeface + 4*4bytes == 0xbabefade
pointers.txt - Albert 给的答案中,都是用“==”来表示结果的
因为在 C 语言中 = 表示赋值
== 表示等于的判断
另外在写的时候,可以使用制表符,这样可能看上去舒服一点
structs.txt - 关于 stderr 的下一句
可以是 exit(1);
return 1;
return EXIT_FAILURE;
为了统一起见,按照老师代码规则,尽量使用 return
因为 Albert 后面的练习答案也是用的 return EXIT_FAILURE;
base2.c - 判断字符串的结尾 '�' 或者 0,两者一样,一个是 char 一个是 int 表示一个东西
prefixes.c
这道题目,Albert 的解法真是厉害,通过对于一个字符串,分别获取第一个字符的和最后一个字符的指针
然后将最后一个字符逐渐向前移动,并且每次重新赋值最后一个字符为 '�'
然后分别打印字符串,每次字符串不同,每次都是逐渐变短
Hilarious: 每次通过 sscanf 读取字符串,其实字符可以直接用,毕竟参数就是字符串 argv[]
05. Week05
- 用 malloc 分配内存的时候,可以使用 struct student 也可以用 typedef 的名称 如 Student,以下等效
- malloc(sizeof(struct student))
- malloc(sizeof(Student))
- 所有的指针都需要分配空间,并且后面都需要释放空间 free 指针,一一对应
- 对于 string 分配空间,需要增加一个位置给 '�'
- malloc(sizeof(char)*(strlen(name)+1))
- malloc(sizeof(char)*(strlen(name)+1))
- scanf 读取字符串时候,定义的字符串需要使用数组形式,或者malloc
我自己理解:如果不能直接为字符串赋值,或者不等引用地址的话,就需要malloc分配空间,切记!!!
06. Week06
- 字符串比较使用 strcmp(),不能直接通过 == 来比较,后者是比较地址
args2heap.c - isalnum() ctype.h 用来判断字符是否为字母数字
cHeap.c
07. Week07
- Hamilton cycle and path 没有判断定理
只能自己来具体看
有 Hamilton cycle 肯定有 Hamilton path
Eulerian cycle:度都是偶数
Eulerian path:两个度是奇数,其他都是偶数
HamiltonEuler.txt - 使用 Edge e 的时候,需要判断是否有效,因为如果数字过大,会引起错误的
对于 Graph 或者 LinkedList 等,再补充的时候
要特别注意判断是否为 NULL (虽然基本都不是) - Notice removeE() is static, which mean it is allowed to be called only from within the ADT.
同时需要将 g->nE 减少一个
删除 链表 node 的时候,要考虑是不是删除 head,需要特别考虑(if...else...)
08. Week08
- Spnanning Tree:通过图生成的树,没有回路,必须经过所有顶点
-
a. path
-
smallest: any path with one edge (e.g. a-b or g-m)
-
largest: some path including all nodes (e.g. m-g-h-k-i-j-a-b-c-d-e-f)
-
-
b. cycle
-
smallest: need at least 3 nodes (e.g. i-j-k-i or h-i-k-h)
-
largest: path including most nodes (e.g. g-h-k-i-j-a-b-c-d-e-f-g) (can't involve m)
-
-
c. spanning tree(连接所有顶点的树)
-
smallest: any spanning tree must include all nodes (the largest path above is an example)
-
largest: same
-
-
d. vertex degree
-
smallest: there is a node that has degree 1 (vertex m)
-
largest: in this graph, 5 (b or f)
-
-
e. clique
-
smallest: any vertex by itself is a clique of size 1(任何一个点都满足)
-
largest: this graph has a clique of size 5 (nodes b,c,d,e,f)
GraphFundamentals.txt
-
- 邻接矩阵 Adjacent Matrix
- 邻接链表 Adjacent List
a. nV |6| Adjacency Matrix nE |6| [0] [1] [2] [3] [4] [5] edges |.|----> 0 1 1 0 0 0 1 0 0 1 0 0 1 0 0 1 1 0 0 1 1 0 0 0 0 0 1 0 0 1 0 0 0 0 1 0 b. nV |6| nE |6| Adjacency List edges |.|----> |.|--> 1 --> 2 |.|--> 0 --> 3 --> 4 |.|--> 0 --> 3 |.|--> 1 --> 2 |.|--> 2 --> 5 |.|--> 4GraphRepresentations.txt
- GraphStorageCosts.txt
-
For the purposes of this exercise you may assume:
- a pointer is 8 bytes long, an integer is 4 bytes
- a vertex is an integer
- a linked list node stores an integer
- an adjacency matrix element is an integer
-
For a given graph:
-
Analyse the precise storage cost for the adjacency matrix (AM) representation of a graph of V vertices and E edges.
- Do the same analysis for the adjacency list (AL) representation.
-
Determine the approximate V:E ratio at which point it is more storage efficient to use an AM representation than an AL representation.
- If a graph has 100 vertices, how many edges should it have for AM to be more storage efficient than AL?
-
You can save space by making the adjacency matrix an array of bytes instead of integers. What difference does that make to the ratio?
-
- 【注意】写数学表达式的时候注意乘号,类似编程一样
另外,有些答案好像写反了。。
a. An AM representation requires a V*V matrix of 4 bytes each, regardless of the number of edges. It also requires an array of V pointers. This gives a size of 4*V*V + 8*V. 不需要考虑 edges 本身的地址,因为其与 edges[0] 共用一个地址 b. An AL representation requires an array of V pointers (the starts of the lists), and then one node for each edge in each list. The total number of edges is 2*E. A node is an integer plus a pointer, which is 4+8 bytes. This gives 8*V + 12*2*E. 点会重复,因此需要乘以2 c. So if 8*V + 12*2*E < 4*V*V + 8*V then the AL version requires less storage. Simplifying, if E < V*V/6 then AL requires less storage. 只需要建立不等式即可 If you have a largish graph of 100 vertices, then up to about 1666 edges (which is a lot) it is better to use AL if storage is the main issue. As V gets very large, the factor 6 becomes insignificant. Hence asymptotically if the number of edges is less than V*V then AL is more space efficient than AM. 解不等式即可 d. If the adjacency matrix is just 1 byte instead of 4 bytes, then the formula is E < V*V/24. 原来的4变成1
- DepthAndBreadthFirst.txt
-
Consider the following graph:
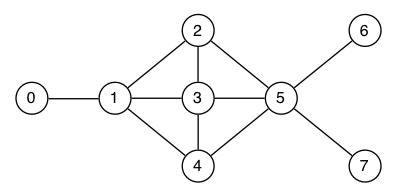
Show the contents of the stack or queue in a 'search' traversal of the graph using:
-
depth-first search starting at vertex 0
-
depth-first search starting at vertex 3
-
breadth-first search starting at vertex 0
-
breadth-first search starting at vertex 3
-
-
对于 stack 和 queue
stack 是 左边压入 左边弹出,push,pop
queue 是 右边压入 左边弹出,qush,pop
stack 是 从大到小 push
queue 是 从小到大 qush
最终目的就是让小的数据先被 pop -
对于 DFS,算法不会加入前面已经 Pop 的点
但是还是会加入存在 stack 内部的点
然后是 top 在左,从 top 往里面放入,从大到小,显示的效果就是小的在上面
从左边压入数据,从左边弹出数据a. DFS starting at 0: Pop Stack (top at left) - 0 0 1. 1 2 3 4. 2 3 5. 3 4 3 4 5. 5 3 4 4 5. 5 5 3 4 5 6 7. 5 5 3 4 6 . 7 5 5 3 4 7 . 5 5 3 4 . where above the '.' shows the newly pushed adjacent vertices b. DFS starting at 3: Pop Stack (top at left) - 3 3 1 2 4 5. 1 0 2 4. 2 4 5 0 . 2 4 2 4 5 2 5. 4 2 4 5 5 4 6 7. 4 2 4 5 4 . 6 7 4 2 4 5 6 . 7 4 2 4 5 7 . 4 2 4 5 . where I've left out the all visited pops
对于 BFS 算法,算法不会加入前面出现过的点
然后是 head 在左,从右边压入数据,从左边弹出
压入数据也是从小到大,显示效果就是小的在前面c. BFS starting at 0: Pop Queue (head at left) - 0 0 . 1 1 . 2 3 4 2 3 4. 5 3 4 5. 4 5. 5 . 6 7 6 7. 7 . d. BFS starting at 3: Pop Queue (head at left) - 3 3 . 1 2 4 5 1 2 4 5. 0 2 4 5 0. 4 5 0. 5 0. 6 7 0 6 7. 6 7. 7 .
- VisitedArray.txt
-
Consider the following 2 graphs (the right graph is missing edge 7-8):
0--1--2 0--1--2 | | | | | | 3--4--5 3--4--5 | | | | | | 6--7--8 6--7 8Starting at vertex 0, and using a depth-first search (assume the smallest vertex is selected):
- compute the visited array for the graph on the left
-
can you deduce a path from vertex 0 to vertex 8 from the visited array?
-
- compute the visited array for the graph on the right
-
can you deduce a path from vertex 0 to vertex 8 from the visited array?
-
Can you draw any conclusions?
- compute the visited array for the graph on the left
-
{{{ 0--1--2 0--1--2 | | | | | | 3--4--5 3--4--5 | | | | | | 6--7--8 6--7 8 }}} a. DFS visited = {0, 1, 2, 5, 4, 3, 6, 7, 8} It is tempting to say that the path is indicated by the visited array, but this is wrong, as we shall see. b. DFS visited = {0, 1, 2, 5, 4, 3, 6, 7, 8} This array is the same as the previous. Clearly the path from vertex 0 to 8 cannot include edge 7--8, so the visited array does not indicate a path. The visited arrays are the same because 'backtracking' is not visible in the visited array: * when DFS reaches vertex 5, it places vertex 8 on the stack, and continues with vertex 4 * when DFS reaches vertex 7, this branch traversal concludes, and it continues with the vertex 8 that remains on the stack * it does not matter whether there is an edge 7-8 or not, the visited arrays are identical Conclusion: a visited array does not show the path
09. Week09
- Dijkstra.txt
-
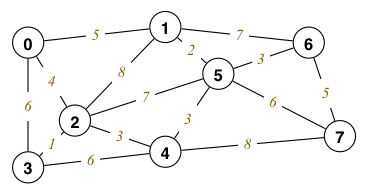
Dijkstra's algorithm computes the minimum path costs from the source node 0 to all the other vertices, resulting in the Shortest Path Tree (SPT). For the following graph:
-
show the order that vertices are visited, and the path cost pacost[] of each of the vertices
- (when faced with a choice, select the edge to the lowest vertex)
-
there are 4 vertices that undergo non-trivial edge relaxation. What are they, and what is the reduction in cost for each vertex?
- draw the SPT
-
-
a. 按照访问顺序填写,pacost[0] = 0.00,另外注意是 float
b. non-trivial 表示具体数字的变化,注意符号 ==>,以及 float
c. 绘制 SPT 的时候,尽量按照具体数字顺序,小的在左,大的在右Actions taken by Dijkstra's Algorithm a. The visit order of the vertices, together with the path costs visit 0, pacost[0] = 0.00 visit 2, pacost[2] = 4.00 visit 1, pacost[1] = 5.00 visit 3, pacost[3] = 5.00 visit 4, pacost[4] = 7.00 visit 5, pacost[5] = 7.00 visit 6, pacost[6] = 10.00 visit 7, pacost[7] = 13.00 b. The 4 vertices that are relaxed are 3, 5, 6 and 7 pacost[3] = 6.00 ==> 5.00 pacost[5] = 11.00 ==> 7.00 pacost[6] = 12.00 ==> 10.00 pacost[7] = 15.00 ==> 13.00 c. The SPT is: 0 / 1 2 | / 5 3 4 / 6 7 - Prim.txt
-
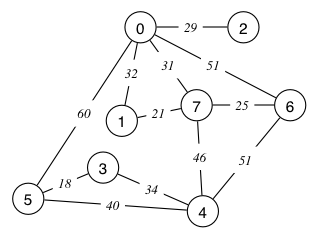
Prim's Algorithm generates a Minimum Spanning Tree (MST). For the following graph:
-
by hand, use the sets mst and rest to build an MST one vertex at a time Do this in the form of a table, where the first 2 lines have been completed for you.
mst
rest vertex
cost
{0}
2
29
{0,2}
7
31
...
...
...
- draw the MST
- how many edges in the MST?
- what is the cost of the MST?
-
-
Actions taken by Prim's Algorithm using sets MST and REST a. new MST vertex cost {0} 2 29 {0,2} 7 31 {0,2,7} 1 21 {0,2,7,1} 6 25 {0,2,7,1,6} 4 46 {0,2,7,1,6,4} 5 18 {0,2,7,1,6,4,5} b. 0 / 2 7 / | 1 6 4 | 3 | 5 c. 7 edges d. cost is 204 - Kruskal.txt
-
Kruskal's Algorithm also generates an MST. For the following graph:
- show which edges are considered at each step and ...
- whether the edge gets accepted, or rejected (because it causes a cycle)
- draw the MST.
- is the MST the same of different to the MST generated by Prim's algorithm?
-
-
【注意】cost 用 float 表示,另外就是格式
还有就是 Prim 和 Kruskal 算法的结果一致Actions taken by Kruskal's algorithm a. Accept 3-5: 18.00 Accept 1-7: 21.00 Accept 6-7: 25.00 Accept 0-2: 29.00 Accept 0-7: 31.00 Reject 0-1: 32.00 Accept 3-4: 34.00 Reject 4-5: 40.00 Accept 4-7: 46.00 b. Same as Prim's MST. - stdin 的时候,就是 通过 scanf() 或者 getchar() 等按照顺序读取
对于第一次开始的 white space 不能直接跳过,通过下面代码跳过
上面的代码可以跳过开头不确定的 空格、制表符、回车键 等。char space[100]; scanf("%[ /t/n]", space);
然后继续读取井号,通过 getchar() 实现
一次只读取一个字符,然后通过 scanf() 每次读取一对数据,这地方对于格式有要求
判断条件可以是 scanf("%d %d", &v1, &v2) != EOF
也可以是 scanf("%d %d", &v1, &v2) == 2
经验证,两种方法均可
#6 0 1 0 2 1 2 3 4 3 5 4 5 - 实现代码:
-
// By Alex int read_num() { char space[100]; scanf("%[ /t/n]", space); getchar(); int num; scanf("%d", &num); return num; } Graph read_graph(int nV) { int v, w; Graph g; g = newGraph(nV); while (scanf("%d %d", &v, &w) != EOF) { //while (scanf("%d %d", &v, &w) == 2) { Edge e; e = newE(v, w); insertE(g, e); } return g; } -
// By Albert #define WHITESPACE 100 int readNumV(void) { // returns the number of vertices numV or -1 int numV; char w[WHITESPACE]; scanf("%[ ]s", w); // skip leading whitespace if ((getchar() != '#') || (scanf("%d", &numV) != 1)) { fprintf(stderr, "missing number (of vertices) "); return -1; } return numV; } int readGraph(int numV, Graph g) { // reads number-number pairs until EOF int success = true; // returns true if no error int v1, v2; while (scanf("%d %d", &v1, &v2) != EOF && success) { if (v1 < 0 || v1 >= numV || v2 < 0 || v2 >= numV) { fprintf(stderr, "unable to read edge "); success = false; } else { insertE(g, newE(v1, v2)); } } return success; } - 使用 iteration 实现 unreachable
思路,首先将 visited[0] = 1,其他均为访问
然后无限循环,从里面找一个未访问的节点,然后便利其邻接点,若存在访问过的节点
则标记一下,另外就是标记这个点访问过,直到退出循环
// By Alex int main() { int nV = read_num(); Graph g = read_graph(nV); showGraph(g); int visited[nV]; visited[0] = 1; for (int i = 1; i < nV; i++) { visited[i] = 0; } int one_graph_all_vis = 0; while (!one_graph_all_vis) { one_graph_all_vis = 1; for (int v = 0; v < nV; v++) { if (!visited[v]) { for (int w = 0; w < nV; w++) { if (visited[w] && isEdge(g, newE(v, w))) { visited[v] = 1; one_graph_all_vis = 0; } } } } } int unreachable = 0; for (int i = 0; i < nV; i++) { if (!visited[i]) { unreachable = 1; } } if (unreachable) { printf("Unreachable vertices = "); for (int i = 0; i < nV; i++) { if (!visited[i]) { printf("%d ", i); } } putchar(' '); } else{ printf(" Unreachable vertices = none "); } return 0; }
10. Week10
- Heap-Order Property (sometimes called HOP)
Complete-Tree Property (sometimes called CTP)
a. BST because it has Left-Right order b. Heap because it satisfies HOP and CTP c. Heap because it satisfies HOP and CTP d. It is neither a BST nor a heap. It is just a binary tree. e. Could be either. It has L-R order, and it satisfies the HOP and CTP. f. Could be either. It has L-R order, and it satisfies the HOP and CTP
- BSTrootleafinsert.txt
-
Consider an initially empty BST and the sequence of values 1 2 3 4 5 6.
-
Show the tree resulting from inserting these values "at the leaf". What is its height?
-
Show the tree resulting from inserting these values "at the root". What is its height?
-
Show the tree resulting from an alternate at-root-insertion and at-leaf-insertion, starting with at-the-leaf. What is its height?
-
-
说明:at the leaf:说明直接插入到 leaf 即可,不需要移动
at the root:说明需要调整到 root,但是一个一个调整
- Splaying.txt
- Given an initially empty splay tree:
-
show the changes in the splay tree after each splay-insertion of the node values 5 3 8 7 4
-
- Given an initially empty splay tree:
-
show the changes in the splay tree after each splay-insertion of the node values b c d e f g ...
-
and then the splay tree after a search for node a ...
-
and then the splay tree after a search for node d
说明:如果 search 不到元素,就将那个元素 splay,按照 zigzag 或者 zigzig 规则操作
-