灯塔(LightHouse)

灯塔(LightHouse)

---

Description

As shown in the following figure, If another lighthouse is in gray area, they can beacon each other.

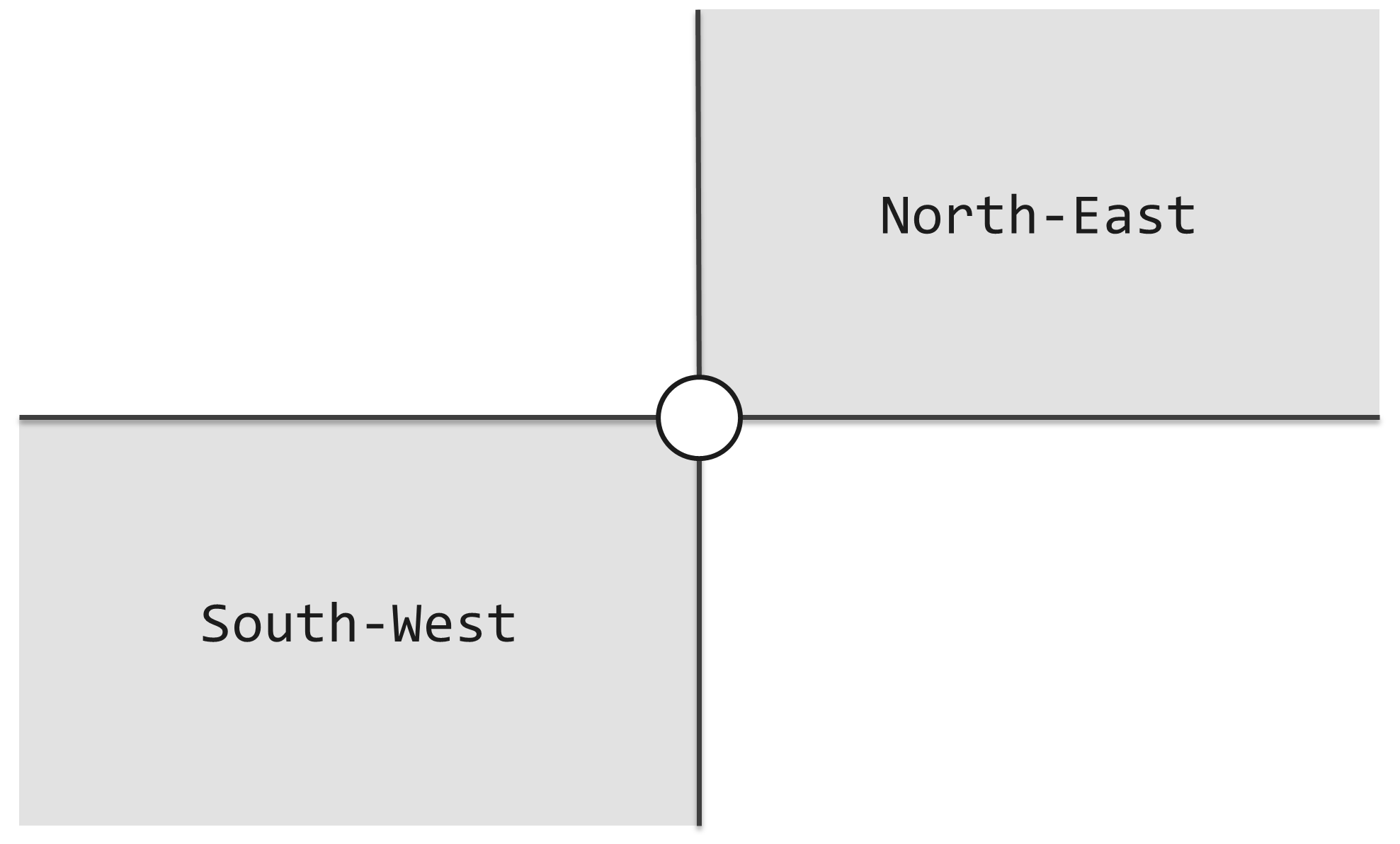
For example, in following figure, (B, R) is a pair of lighthouse which can beacon each other, while (B, G), (R, G) are NOT.

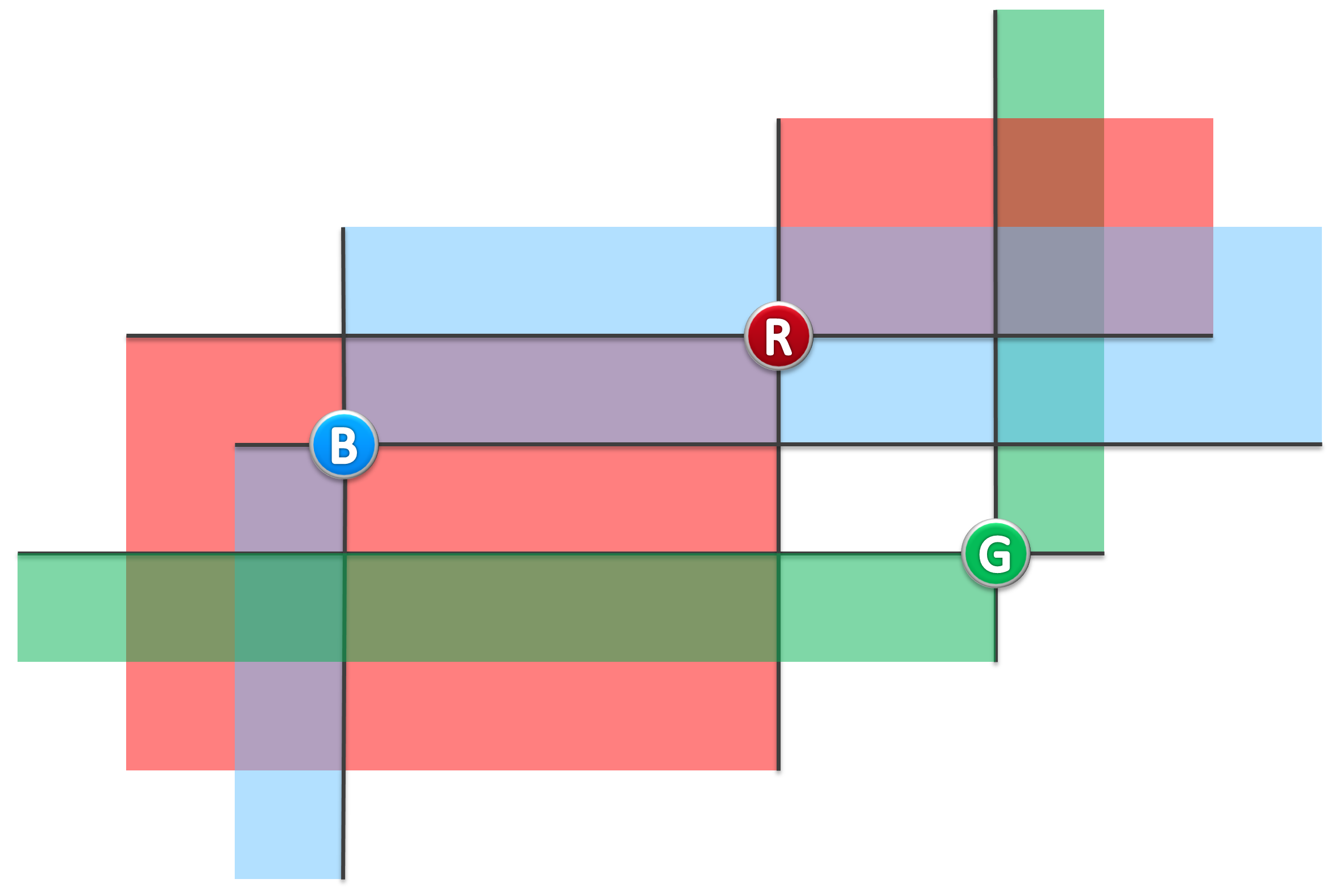
Input

1st line: N

2nd ~ (N + 1)th line: each line is X Y, means a lighthouse is on the point (X, Y).

Output

How many pairs of lighthourses can beacon each other

( For every lighthouses, X coordinates won't be the same , Y coordinates won't be the same )

Example

Input

3
2 2
4 3
5 1

Output

1

Restrictions

For 90% test cases: 1 <= n <= 3 * 105

For 95% test cases: 1 <= n <= 106

For all test cases: 1 <= n <= 4 * 106

For every lighthouses, X coordinates won't be the same , Y coordinates won't be the same.

1 <= x, y <= 10^8

Time: 2 sec

Memory: 256 MB

Hints

The range of int is usually [-231, 231 - 1], it may be too small.

1. 原理与要点： 根据题意，一个点可以看见位于其右上方的点。先按照x从小到大，如果x相同就y从小到大的次序排序。显然，排序后的序列中若(y_j>y_i(j>i)) ，则i与j两个灯塔可以互相照到。能够互相照到的灯塔对数也就是排序后序列中的顺序对数。用归并排序进行排序，在排序的过程中求顺序对。
2. 遇到的问题：无
3. 时间和空间复杂度： 时间复杂度(O(nlogn))，空间复杂度(O(n))

#include "iostream"
#include "cstdio"
#include "cstring"

using namespace std;


const int SZ = 1<<20;  //快速io
struct fastio{
    char inbuf[SZ];
    char outbuf[SZ];
    fastio(){
        setvbuf(stdin,inbuf,_IOFBF,SZ);
        setvbuf(stdout,outbuf,_IOFBF,SZ);
    }
}io;

const int maxn = 4e6 + 100;
typedef long long ll;
struct node {
    int x, y;
} a[maxn], b[maxn];
ll ans = 0;

void merge1(int l, int mid, int r) {
    if (l == r) return;
    merge1(l, (l + mid) >> 1, mid);
    merge1(mid + 1, (mid + 1 + r) >> 1, r);
    int i = l, j = mid + 1;
    for (int k = l; k <= r; k++) {
        if (j > r || (i <= mid && (a[i].x < a[j].x || (a[i].x == a[j].x && a[i].y < a[j].y)))) b[k] = a[i++];
        else b[k] = a[j++];
    }
    for (int k = l; k <= r; k++)
        a[k] = b[k];
}

void merge2(int l, int mid, int r) {
    if (l == r) return;
    merge2(l, (l + mid) >> 1, mid);
    merge2(mid + 1, (mid + 1 + r) >> 1, r);
    int i = l, j = mid + 1;
    for (int k = l; k <= r; k++) {
        if (j > r || (i <= mid && a[i].y < a[j].y)) b[k] = a[i++], ans += r - j + 1;
        else b[k] = a[j++];
    }
    for (int k = l; k <= r; k++)
        a[k] = b[k];
}

int main() {
    ll n;
    scanf("%lld", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d %d", &a[i].x, &a[i].y);
    }
    merge1(1, (1 + n) >> 1, n);
    merge2(1, (1 + n) >> 1, n);
    printf("%lld
", ans);
    return 0;
}