交换机器的最小代价

一、问题描述

有N台机器重量各不相等，现在要求把这些机器按照重量排序，重量从左到右依次递增。移动机器只能做交换操作，但交换机器要花费一定的费用，费用的大小就是交换机器重量的和。例如：3 2 1，交换1 3后为递增排序，总的交换代价为4。
给出N台机器的重量，求将所有机器变为有序的最小代价（机器的重量均为正整数）。

输入
第1行：1个数N，表示机器及房间的数量。（2 <= N <= 50000)
第2 - N + 1行：每行1个数，表示机器的重量Wi。(1 <= Wi <= 10^9)

输出
最小代价

样例1输入

5
1 
8 
9
7
6

样例1输出

41

二、思路

以样例1例，先进行排序

下标	1	2	3	4	5
排序前	1	8	9	7	6
排序后	1	6	7	8	9

我们从元素1开始看，排序后元素1的位置还是1，那么就给1到1之间连一条边，形成一个自环；再到元素8，元素8排序以后到了第4个位置，而第四个位置是元素7，所以给8到7之间连一条有向边，同理连完剩下的边可以得到一张图：

 

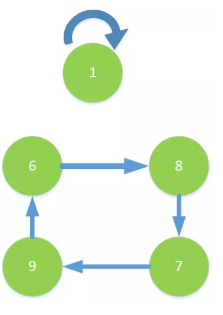
那么我们可以发现两个环，那么我们回到题目中来，要使最后的总和最小，我们的贪心思路是什么？
策略一：
对于每一个环的贪心思路就是，找到这个环中最小的那个点，也就是6，然后从6开始进行交换，6和9交换，可以使9到对应的位置，花费为6+9=15,然后6和7交换，花费为6+7=13，最后等到交换完毕，自最后的答案是什么呢？就是：
(6+9)+(6+7)+(6+8) = (6+7+8+9)+6∗2 = 30+12 = 42。
剩下一个环不用交换，那么当前的最小值就是42，但是这不一定是最优解。
这种策略的解可表示为ans1 = sum + min * (cnt - 1)，这里min是当前环中的最小值，cnt是min与别的元素交换的次数。

策略二:

 

在这个图中找到一个最小的值，然后用这个值跟着当前的环进行交换，在这个图中很明显是1，我们让第1和第二个环中的最小值6进行交换，然后再像上面一样，交换1和9，花费为:1+9=10，交换1和7，花费为：1+7=8等到交换完毕，最后的结果是:
(1+6)+(1+9)+(1+7)+(1+8)+(1+6) = (6+8+7+9)+1∗5+6 = 41
这种策略的解可表示为ans2 = sum + least * (cnt + 2) + min，这里least表示所有元素的最小值，min表示当前环中的最小值。
我们的贪心策略就是在这两个策略之间，找出一个最小值ans = min(ans1, ans2)。

三、代码

#include<iostream>
#include<algorithm>
#define MAXN 50010
using namespace std;

bool visited[MAXN]; //记录该位置的机器是否已经排好序
int least;//记录最小重量

struct machine
{
    int origin;//原来的位置
    int weight;//机器的重量
};
machine mac[MAXN];

bool cmp(machine a, machine b)
{
    return a.weight < b.weight;
}

long long solve(int i)
{
    visited[i] = true;
    int MIN = mac[i].weight;
    long long sum = mac[i].weight;
    int j = mac[i].origin;
    int cnt = 0;

    while(i != j)
    {
        sum += mac[j].weight;
        MIN = min(MIN,mac[j].weight);
        visited[j] = true;
        j = mac[j].origin;
        cnt++; //计算需要交换的机器数量
    }

    return sum + min((long long)MIN*(cnt-1), (long long)least*(cnt+2)+MIN);//两种策略的比较
}

int main()
{
    int n;
    long long ans=0;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>mac[i].weight;
        mac[i].origin=i;
    }

    sort(mac+1, mac+n+1, cmp);

    least = mac[1].weight;

    for(int i=1; i<=n; i++)
    {
        if(!visited[i])
        {
            ans += solve(i);
        }
    }

    cout << ans << endl;

    return 0;
}