Road To The 3rd Building
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 524288/262144 K (Java/Others)
链接：http://acm.hdu.edu.cn/showproblem.php?pid=6827
题意：给定n棵树，每棵树都有自己的“美丽值”,第k棵树的美丽值为sk。已知一条路径是从第i课树走到第j棵树，i<=j，这条路径的美丽值为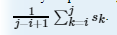
求所有路径的期望值，答案mod 10^9+7.
数据范围：T个样例
保证所有样例的n总和不超过10^6
题解：列表观察每一棵树被计算的次数，可以发现规律：
N=7
树的编号i
1 2 3 4 5 6 7
分母大小 1 1 1 1 1 1 1 1
2 1 2 2 2 2 2 1
3 1 2 3 3 3 2 1
4 1 2 3 4 3 2 1
5 1 2 3 3 3 2 1
6 1 2 2 2 2 2 1
7 1 1 1 1 1 1 1
N=6
树的编号i
1 2 3 4 5 6
分母大小 1 1 1 1 1 1 1
2 1 2 2 2 2 1
3 1 2 3 3 2 1
4 1 2 3 3 2 1
5 1 2 2 2 2 1
6 1 1 1 1 1 1
可以发现，计算次数是呈矩形逐渐缩小的。利用这个规律，用suminv数组记录逆元前缀和，sum数组记录树的编号前缀和，逐级相乘即可。
计算的时候没有注意到逆元前缀和能用线性求逆元计算，不过时间也没慢多少。（别骂了，我知道我是菜鸡）
suminv相减一定要注意负值得问题。一开始觉得最后结果时处理负数就可以了，样例和手造样例也过了，结果wa了几发，过了一会才发现这个问题。
1 #include <bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 #define ull unsigned long long 5 //#define LOCAL 6 const int N = 2 * 100000 + 5; 7 const int mod = 1e9 + 7; 8 ll s[N], sum[N]; 9 ll inv[N], suminv[N]; 10 ll ans; 11 inline ll qpow(int a, long long b) 12 { 13 ll c = 1; 14 for (; b; b >>= 1) 15 { 16 if (b & 1) 17 c = (ll)c * a % mod; 18 a = (ll)a * a % mod; 19 } 20 return c; 21 } 22 inline int read() 23 { 24 int x = 0, f = 1; 25 char ch = getchar(); 26 while (ch < '0' || ch > '9') 27 { 28 if (ch == '-') 29 f = -1; 30 ch = getchar(); 31 } 32 while (ch >= '0' && ch <= '9') 33 { 34 x = (x << 1) + (x << 3) + (ch ^ 48); 35 ch = getchar(); 36 } 37 return x * f; 38 } 39 inline void init() 40 { 41 for (int i = 1; i <= N; i++) 42 { 43 inv[i] = qpow(i, mod - 2); 44 suminv[i] = suminv[i - 1] + inv[i]; 45 if (suminv[i] >= mod) 46 suminv[i] -= mod; 47 } 48 } 49 int main() 50 { 51 #ifdef LOCAL 52 freopen("in.txt", " r", stdin); 53 // freopen("out.txt", " w", stdout); 54 #endif 55 init(); 56 int T = read(); 57 while (T--) 58 { 59 int n = read(); 60 for (int i = 1; i <= n; i++) 61 { 62 63 s[i] = read(); 64 sum[i] = sum[i - 1] + s[i]; 65 } 66 ans = 0; 67 int l = (n >> 1); 68 69 for (int i = 1; i <= (n & 1 ? l + 1 : l); i++) 70 { 71 ll qaq = suminv[n - i + 1] - suminv[i - 1]; 72 if(qaq<0) 73 qaq += mod; 74 ans += qaq % mod * ((sum[n - i + 1] - sum[i - 1]) % mod) % mod; 75 ans %= mod; 76 } 77 78 ans *= 2 * inv[n] % mod * inv[n + 1] % mod; 79 ans %= mod; 80 if (ans < 0) 81 ans += mod; 82 printf("%lld ", ans); 83 } 84 }