暴力写挂[CTSC2018]

题目描述

给定两棵树 (T) 和 (T')

求

[max(mathrm{depth}(x) + mathrm{depth}(y) - ({mathrm{depth}(mathrm{LCA}(x,y))}+{mathrm{depth'}(mathrm{LCA'}(x,y))})) ]

注：带[ (') ]的表示第二棵树

题解

注意到题目给的这个

[mathrm{depth}(x) + mathrm{depth}(y) - {mathrm{depth}(mathrm{LCA}(x,y))}-{mathrm{depth'}(mathrm{LCA'}(x,y))} ]

似乎不太好算

我们把前3项转换一下 发现上面这个式子实际上等于

[dfrac{1}{2}(mathrm{depth}(x) + mathrm{depth}(y) + mathrm{dis}(x,y) - 2 * {mathrm{depth'}(mathrm{LCA'}(x,y))}) ]

这样一来，前三项可以通过边分治处理出来，然后最后一项则需要在第二棵树上来计算

具体地说，我们对第一棵树进行边分治，然后将当前分治边左边的点标为黑点，右边标为白点

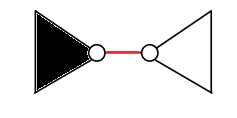
假设一个点(x)到分治边的距离为(mathrm{d}(x))，分治边的长度是(v)，那么上面式子的前3项实际上就等于(mathrm{depth}(x) + mathrm{depth}(y) + (mathrm{d}(x) + mathrm{d}(y) + v))

所以把每个点的点权(mathrm{val}(x))设为(mathrm{depth}(x) + mathrm{d}(x))，然后就可以去处理第二棵树了

在第二棵树中枚举每个点作为lca，那么现在目标就是找到两个颜色不同，且在两个不同儿子子树里的点使得它们的(mathrm{val})之和最大

设(f[x][0])表示(x)子树中最大的黑点权值，(f[x][1])表示最大白点权值；然后就可以在第二棵树上进行dp来得到最大值 具体dp转移见代码

但是dp一次是(O(n))的 所以我们还需要在dp之前对第二棵树建虚树 在虚树上dp

这样总时间复杂度就是(O(nlog^2 n))的 依然会被卡掉。。。

如果想要(O(nlog n))可以加上欧拉序+ST表求LCA以及基数排序建虚树来强行降低复杂度 这里我只写了个(O(1))求LCA 吸氧后勉强卡过 基数排序什么的表示不懂

代码难度非常非常大 写到心态爆炸

代码

#include <bits/stdc++.h>
#define NN 370005
using namespace std;
typedef long long ll;

template<typename T>
inline void read(T &num) {
	T x = 0, f = 1; char ch = getchar();
	for (; ch > '9' || ch < '0'; ch = getchar()) if (ch == '-') f = -1;
	for (; ch <= '9' && ch >= '0'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ '0');
	num = x * f;
}

int n, q[NN], tp[NN], tot;
ll ww[NN], ans = -0x3f3f3f3f3f3f3f3f;
namespace p2{
	int head[NN], dfn[NN], pre[NN<<1], to[NN<<1], sz = 1, tme;
	ll val[NN<<1];
	
	inline void addedge(int u, int v, int w) {
		pre[++sz] = head[u]; head[u] = sz; to[sz] = v; val[sz] = w;
		pre[++sz] = head[v]; head[v] = sz; to[sz] = u; val[sz] = w;
	}
	
	int d[NN], p[1000005][21], lg2[1000005];
	int stk[NN], top;
	ll dep[NN], f[NN][2];
	bool tag[NN];
	
	void dfs(int x, int fa) {
		p[++tme][0] = x;
		dfn[x] = tme;
		for (int i = head[x]; i; i = pre[i]) {
			int y = to[i];
			if (y == fa) continue;
			d[y] = d[x] + 1;
			dep[y] = dep[x] + val[i];
			dfs(y, x);
			p[++tme][0] = x;
		}
	}
	
	inline int LCA(int x, int y) {
		if (dfn[x] > dfn[y]) swap(x, y);
		int l = dfn[x], r = dfn[y], len = dfn[y] - dfn[x] + 1;
		if (d[p[l][lg2[len]]] < d[p[r-(1<<lg2[len])+1][lg2[len]]]) {
			return p[l][lg2[len]];
		} else return p[r-(1<<lg2[len])+1][lg2[len]];
	}
	
	void init() {
		dfs(1, 0);
		for (int i = 2; i <= tme; i++) lg2[i] = lg2[i>>1] + 1;
		for (int l = 1; (1 << l) <= tme; l++) {
			for (int i = 1; i <= tme; i++) {
				if (d[p[i][l-1]] < d[p[i+(1<<(l-1))][l-1]]) {
					p[i][l] = p[i][l-1];
				} else p[i][l] = p[i+(1<<(l-1))][l-1];
			} 
		}
		memset(head, 0, sizeof(head));
		sz = 1;
	}
	
	bool cmp(int x, int y) {
		return dfn[x] < dfn[y];
	}
	
	void buildtree() {
		sz = 1;
		sort(q + 1, q + tot + 1, cmp);
		for (int i = 1; i <= tot; i++) tag[q[i]] = 1;
		stk[top=1] = 1;
		for (int i = 1; i <= tot; i++) {
			if (q[i] == 1) continue;
			if (top == 1) {
				stk[++top] = q[i]; 
				continue;
			}
			int lca = LCA(stk[top], q[i]);
			while (top > 1 && dfn[stk[top-1]] >= dfn[lca]) {
				addedge(stk[top], stk[top-1], 0);
				top--;
			}
			if (lca != stk[top]) {
				addedge(stk[top], lca, 0);
				stk[top] = lca;
			}
			stk[++top] = q[i];
		}
		while (top > 1) {
			addedge(stk[top], stk[top-1], 0);
			top--;
		}
	}
	
	void dp(int x, int fa, ll len) {
		f[x][0] = f[x][1] = -0x3f3f3f3f3f3f3f3f;
		if (tag[x]) f[x][tp[x]] = ww[x];
		for (int i = head[x]; i; i = pre[i]) {
			int y = to[i];
			if (y == fa) continue;
			dp(y, x, len);
			ll now = max(f[x][0] + f[y][1], f[x][1] + f[y][0]);
			ans = max(ans, len + now - 2 * dep[x]);
			f[x][0] = max(f[x][0], f[y][0]);
			f[x][1] = max(f[x][1], f[y][1]);
		} 
		tag[x] = 0; head[x] = 0;
	}
	
	void solve(ll len) {
		buildtree();
		dp(1, 0, len);
	}
}

namespace p1{
	int head[NN<<2], pre[NN<<3], to[NN<<3], sz = 1, N;
	ll val[NN<<3];
	vector<pair<int, ll> > son[NN<<2];
	bool vis[NN<<2];
	int siz[NN<<2], ct, mn, sum;
	ll dep[NN<<2];
	
	inline void addedge(int u, int v, ll w) {
		pre[++sz] = head[u]; head[u] = sz; to[sz] = v; val[sz] = w;
		pre[++sz] = head[v]; head[v] = sz; to[sz] = u; val[sz] = w;
	}
	
	void dfs1(int x, int fa) {
		for (int i = head[x]; i; i = pre[i]) {
			int y = to[i];
			if (y == fa) continue;
			son[x].push_back(make_pair(y, val[i]));
			dep[y] = dep[x] + val[i];
			dfs1(y, x);
		}
	}
	
	void rebuild() {
		memset(head, 0, sizeof(head)); sz = 1;
		for (int i = 1; i <= N; i++) {
			int k = son[i].size();
			if (k <= 2) {
				for (int j = 0; j < k; j++) {
					addedge(i, son[i][j].first, son[i][j].second);
				}
			} else {
				addedge(i, ++N, 0); addedge(i, ++N, 0);
				for (int j = 0; j < k; j++) {
					if (j & 1) son[N-1].push_back(son[i][j]);
					else son[N].push_back(son[i][j]);
				}
			}
		}
	}
	
	void findct(int x, int fa) {
		siz[x] = 1;
		for (int i = head[x]; i; i = pre[i]) {
			int y = to[i];
			if (y == fa || vis[i>>1]) continue;
			findct(y, x);
			siz[x] += siz[y];
			int now = max(siz[y], sum - siz[y]);
			if (now < mn) {
				mn = now;
				ct = i;
			}
		}
	}
	
	void dfs(int x, int fa, ll dis, int o) {
		if (x <= n) {
			q[++tot] = x;
			ww[x] = dep[x] + dis;
			tp[x] = o;
		}
		for (int i = head[x]; i; i = pre[i]) {
			int y = to[i];
			if (y == fa || vis[i>>1]) continue;
			dfs(y, x, dis + val[i], o);
		}
	}
	
	void divide(int x, int _siz) {
		ct = 0; mn = 0x7fffffff; 
		sum = _siz;
		findct(x, 0);
		if (!ct) return;
		vis[ct>>1] = 1;
		int l = to[ct], r = to[ct^1];
		tot = 0;
		dfs(l, 0, 0, 0); dfs(r, 0, 0, 1);
		if (!tot) return;
		p2::solve(val[ct]);
		divide(l, siz[to[ct]]); divide(r, _siz - siz[to[ct]]);
	}
}


int main() {
	read(n); 
	p1::N = n;
	for (int i = 1, u, v, w; i < n; i++) {
		read(u); read(v); read(w);
		p1::addedge(u, v, w);
	}	
	for (int i = 1, u, v, w; i < n; i++) {
		read(u); read(v); read(w);
		p2::addedge(u, v, w);
	}
	p1::dfs1(1, 0);
	p1::rebuild();
	p2::init();
	p1::divide(1, p1::N);
	ans >>= 1;
	for (int i = 1; i <= n; i++) {
		ans = max(ans, p1::dep[i] - p2::dep[i]);
	}
	printf("%lld
", ans);
	return 0;
}