.....好吧....最后一篇学习笔记的flag它倒了.....
好吧,这篇笔记也鸽了好久好久了...
比赛前刷模板,才想着还是补个坑吧...
FHQ,这个神仙(范浩强大佬),发明了这个神仙的数据结构,
首先,本篇博客使用洛谷普通平衡树为背景,即
- 查找前驱
- 查找后记
- 查找kth的数
- 查找k的排名
- 插入一个数
- 删除一个数
FHQ treap,是一个treap,它还是和treap一样,是tree+heap,所以它也有一个键值维护堆的性质。
它可以干任何treap和Splay能干的事。
它的实现主要由两个函数实现:
merge:把两棵树合并成一棵
split:把树分割成两棵
在这里介绍两个函数的实现方法:
merge
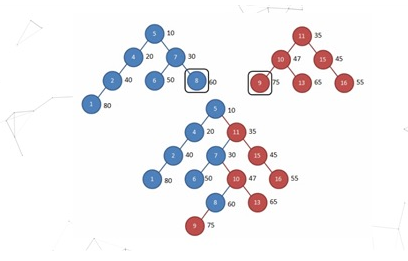
可以看到,它把两棵树合并了起来,但是并不是简单地接起来,而是打散,重新组合。
代码:

int merge(int x,int y)//把xy为根的两棵子树给合并
{
if(!x||!y)//如果一边没了
return x+y;//就返回
if(t[x].key<t[y].key)//维护key值,如果x的key值小于y的k值
{
t[x].son[1]=merge(t[x].son[1],y);//说明此时一定不符合堆性质,把x的右儿子和y合并
update(x);//更新相关变量
return x;//返回根节点
}
else
{
t[y].son[0]=merge(x,t[y].son[0]);//同上
update(y);
return y;
}
}
通过这样一个递归,不断拆分节点&&合并的过程中,就建立了一棵新树。
split:
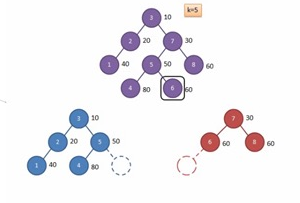
从上图可得:(把树从5分开)
split的过程就是把树拆分成左右树,左树所有节点权值都小于k,右树的节点权值都大于k。
怎么实现呢?
代码:

void split(int now,int k,int &x,int &y)//把一棵树now给从k分割成x和y
{
if(!now) x=y=0;//如果没有了,就返回
else
{
if(t[now].v<=k) //如果当前点的权值小于k,它应该在左子树
{
x=now;//更新
split(t[now].son[1],k,t[now].son[1],y);分割右儿子,找一个可能的更大的
}
else//同上
{
y=now;
split(t[now].son[0],k,x,t[now].son[0]);
}
update(now);
}
}
这样,我们就可以干以上的事了。
前置:查找kth
因为建立的事一个二叉查找树,所以还是可以像遍历二叉查找树那样查找kth的。
代码十分简单

int kth(int now,int k)
{
while(1)
{
if(k<=t[t[now].son[0]].size)
now=t[now].son[0];
else
{
if(k==t[t[now].son[0]].size+1)
return now;
else
{
k-=t[t[now].son[0]].size+1;
now=t[now].son[1];
}
}
}
}
然后就可以A掉普通平衡树了。
插入新节点:首先暴力新建一个节点

int new_node(int k)
{
tot++;
t[tot].size=1;
t[tot].v=k;
t[tot].key=rand();
return tot;
}
然后把树从k地方断开,把新节点看做一棵树,把它和上下树合在一起就行了

split(rt,a,x,y);
rt=merge(merge(x,new_node(a)),y);
删除节点:
把树从k断开,然后把左树从k-1断开,然后把上下树给合并,把k节点扔了就行了

split(rt,a,x,z);
split(x,a-1,x,y);
y=merge(t[y].son[0],t[y].son[1]);
rt=merge(merge(x,y),z);
查找排名:
把树从k分开,则k所在的数的size即使排名

split(rt,a-1,x,y);
printf("%d
",t[x].size+1);
rt=merge(x,y);
查找kth:
直接用kth函数即可

printf("%d
",t[kth(rt,a)].v);
前驱:
把树从k分开,则size-1大小的那个kth点就是前驱

split(rt,a-1,x,y);
printf("%d
",t[kth(x,t[x].size)].v);
rt=merge(x,y);
后继:同上

split(rt,a,x,y);
printf("%d
",t[kth(y,1)].v);
rt=merge(x,y);
完整高清无码代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+10;
struct tree
{
int son[2],v,key,size;
}t[maxn];
int tot=0,rt=0;
void update(int p)
{
t[p].size=t[t[p].son[0]].size+t[t[p].son[1]].size+1;
}
int new_node(int k)
{
tot++;
t[tot].size=1;
t[tot].v=k;
t[tot].key=rand();
return tot;
}
int merge(int x,int y)//o?2¢ò?x£?y?a?ùμ?á???×óê÷
{
if(!x||!y)
return x+y;
if(t[x].key<t[y].key)
{
t[x].son[1]=merge(t[x].son[1],y);
update(x);
return x;
}
else
{
t[y].son[0]=merge(x,t[y].son[0]);
update(y);
return y;
}
}
void split(int now,int k,int &x,int &y)//ò?è¨?μk·?à?nowê÷3éx,y
{
if(!now) x=y=0;
else
{
if(t[now].v<=k) //°??ùóDD?óúkμ?è¨?μμ??úμ?·?μ?ò???ê÷?D
{
x=now;
split(t[now].son[1],k,t[now].son[1],y);
}
else
{
y=now;
split(t[now].son[0],k,x,t[now].son[0]);
}
update(now);
}
}
int kth(int now,int k)
{
while(1)
{
if(k<=t[t[now].son[0]].size)
now=t[now].son[0];
else
{
if(k==t[t[now].son[0]].size+1)
return now;
else
{
k-=t[t[now].son[0]].size+1;
now=t[now].son[1];
}
}
}
}
int x,y,z,n;
int main()
{
srand((unsigned)time(NULL));
scanf("%d",&n);
int flag,a,b,c;
for(int i=1;i<=n;i++)
{
scanf("%d",&flag);
scanf("%d",&a);
if(flag==1)
{
split(rt,a,x,y);
rt=merge(merge(x,new_node(a)),y);
}
if(flag==2)
{
split(rt,a,x,z);
split(x,a-1,x,y);
y=merge(t[y].son[0],t[y].son[1]);
rt=merge(merge(x,y),z);
}
if(flag==3)
{
split(rt,a-1,x,y);
printf("%d
",t[x].size+1);
rt=merge(x,y);
}
if(flag==4)
{
printf("%d
",t[kth(rt,a)].v);
}
if(flag==5)
{
split(rt,a-1,x,y);
printf("%d
",t[kth(x,t[x].size)].v);
rt=merge(x,y);
}
if(flag==6)
{
split(rt,a,x,y);
printf("%d
",t[kth(y,1)].v);
rt=merge(x,y);
}
}
return 0;
}
