
(我恨字符串)
惯例化简题目:给定n个字符串,可以改变字符的相对大小(在字典序中的大小),问:字符串i是否能成为最小的字符串(字典序)
解题过程:
- 首先你可以预处理出来26的全排列然后暴力然后你只要用神威太湖之光开O2就能过了
- 秒切字典树
- 推出一堆没用的结论。
说一下思考过程:首先字典树能找前缀都知道吧
- 观察样例,得:对于不能变成第一的,那么一定是有一个跟它有相同前缀的字符串,但是不完全相等,要有比当前串小的。
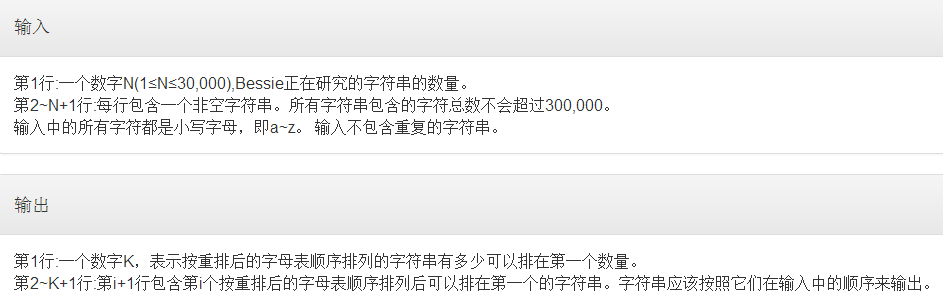
- 然后和旁边大佬一起歪歪瞎搞:建立一棵字典树,然后对于每个字符串跑一遍字典树,如果能找到相同的前缀&&最终终点不在一个分叉上&&分叉比当前串终点小(这里可能要意会一下....算了我上图)
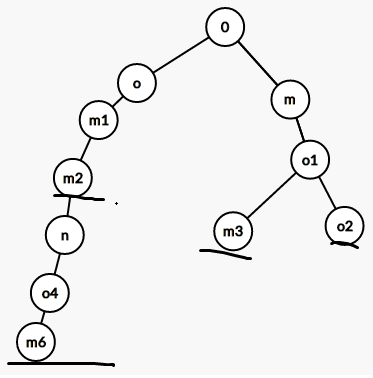
(打标记的是字串结束的地方,软件为了防止重复在相同的字母后加了数字去重,无用)
先看omm,按照上面的结论,很明显可以,其实不然
然后发现....样例打了从样例发现的结论的脸......
solution:
想想怎么判断无解....
一个条件先于另外一个条件....
如果先到自己头上,那就暴毙了。。。
这....拓扑排序??
貌似是这样。
于是,我们在字典树上跑一下,对于一个分支(相同前缀的几个字符)像这样:
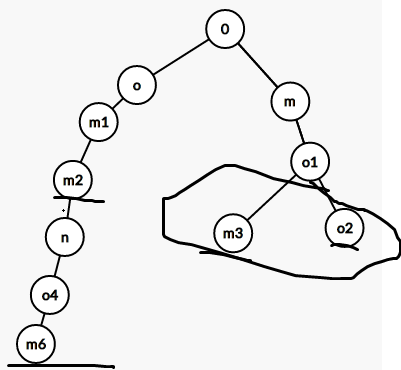
连单向边之后,跑tpsort,如果有环的话(先到自己头上了,不明白自己去学tpsort),那就是一个无解情况
注意,连边不是在树上,而是在字母表上,字母表的每一个都会有初始边(a->b->c->d->e->f->g......->y->z)然后在上述过程中人为加边,然后跑tpsort,一开始我在这里卡住了
然后每个跑就行了,代码没有太大难度,字典树的板子背掉就行了(或者拿临接表硬模)。
代码:(注意,每跑一个要清零。)
#include<bits/stdc++.h> #define register using namespace std; const int maxn=3e5+5; string s[maxn]; struct edge { int to,next; }e[100]; int head[100],cnt; inline void addedge(int from,int to) { e[++cnt].next=head[from]; e[cnt].to=to; head[from]=cnt; } int t[maxn][30]; int vis[maxn]; int used[30][30]; int f; int tot; int ru[100]; int n; int ans[maxn]; int anscnt; inline void update(string x) { int u=0,tt; for( int i=0;i<x.size();i++) { tt=x[i]-'a'; if(!t[u][tt]) { t[u][tt]=++tot; } u=t[u][tt]; } vis[u]=1; } inline void solve(string x) { int u=0,tt; for( int i=0;i<x.size();i++) { tt=x[i]-'a'; if(vis[u]) { f=1; return; } for( int j=0;j<26;j++) { if(t[u][j]&&j!=tt&&!used[tt][j]) { used[tt][j]=1; addedge(tt,j); ru[j]++; } } u=t[u][tt]; } } inline int tpsort() { deque < int > q; for( int i=0;i<26;i++) { if(ru[i]==0) q.push_back(i); } while(!q.empty()) { int u=q.front(); q.pop_front(); for( int i=head[u];i;i=e[i].next) { int v=e[i].to; ru[v]--; if(ru[v]==0) { q.push_back(v); } } } for( int i=0;i<26;i++) { if(ru[i]!=0) return 0; } return 1; } int main() { ios::sync_with_stdio(false); cin>>n; for( int i=1;i<=n;i++) { cin>>s[i]; update(s[i]); } for( int i=1;i<=n;i++) { cnt=0; f=0; memset(head,0,sizeof(head)); memset(ru,0,sizeof(ru)); memset(used,0,sizeof(used)); solve(s[i]); if(f) continue; if(tpsort()) ans[++anscnt]=i; } printf("%d ",anscnt); for(int i=1;i<=anscnt;i++) { printf("%s ",s[ans[i]].c_str()); } return 0; }
(完)