P1955 [NOI2015]程序自动分析 && 离散化学习 && lower_bound学习

题目链接

https://www.luogu.org/problemnew/show/P1955

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设x1,x2,x3...代表程序中出现的变量，给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：x1=x2,x2=x3,x3=x4,x4≠x1，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入输出格式

输入格式：

从文件prog.in中读入数据。

输入文件的第1行包含1个正整数t，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第1行包含1个正整数n，表示该问题中需要被满足的约束条件个数。接下来n行，每行包括3个整数i,j,e，描述1个相等/不等的约束条件，相邻整数之间用单个空格隔开。若e=1，则该约束条件为xi=xj；若e=0，则该约束条件为xi≠xj；

输出格式：

输出到文件 prog.out 中。

输出文件包括t行。

输出文件的第 k行输出一个字符串“ YES” 或者“ NO”（不包含引号，字母全部大写），“ YES” 表示输入中的第k个问题判定为可以被满足，“ NO” 表示不可被满足。

输入输出样例

输入样例#1： 

2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

输出样例#1： 

NO
YES

输入样例#2： 

2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0

输出样例#2： 

YES
NO

说明

【样例解释1】

在第一个问题中，约束条件为：x1=x2,x1≠x2。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：x1=x2,x1=x2。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：x1=x2,x2=x3,x3=x1。只需赋值使得x1=x1=x1，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：x1=x2,x2=x3,x3=x4,x4≠x1。由前三个约束条件可以推出x1=x2=x3=x4，然而最后一个约束条件却要求x1≠x4，因此不可被满足。

【数据范围】

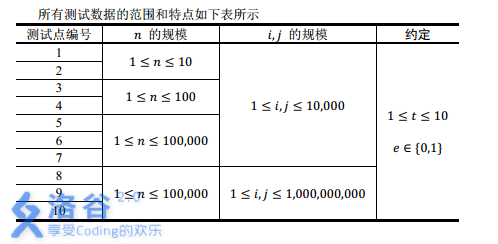
【时限2s，内存512M】

题目分析

这道题是一个很显然的并查集，但是看到数据范围

我们竟然需要开一个1e9的数组！

那么很显然的会MLE

所以我们要用到离散化

然后就可以了qwq

参考代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
//#define DEBUG(x) cerr << #x << "=" << x << endl
const int maxn = 1e5 + 7;

int n, t, f[maxn], book[maxn * 3];

struct node
{
    int x;
    int y;    
    int e;
}a[maxn];

bool cmp(node a, node b)
{
    return a.e > b.e;
}

inline void first(int k)
{
    for (int i = 1; i <= k; i++) f[i] = i; 
}

int get(int x)
{
    return f[x] == x ? x : f[x] = get(f[x]);
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> t;
    while (t--)
    {
        cin >> n;
        int tot = -1;
        int flag = 1;
        memset(a, 0, sizeof(a));
        memset(f, 0, sizeof(f));
        memset(book, 0, sizeof(book));
        for (int i = 1; i <= n; i++)
        {
            cin >> a[i].x >> a[i].y >> a[i].e;
            book[++tot] = a[i].x;
            book[++tot] = a[i].y;
        }
        sort(book, book + tot);
        int reu = unique(book, book + tot) - book;
        for (int i = 1; i <= n; i++)
        {
            a[i].x = lower_bound(book, book + reu, a[i].x) - book;
            a[i].y = lower_bound(book, book + reu, a[i].y) - book;
        }
        first(reu);
        sort(a + 1, a + n + 1, cmp);
        for (int i = 1; i <= n; i++)
        {
            int r1 = get(a[i].x);
            int r2 = get(a[i].y);
            if (a[i].e)
            {
                f[r1] = r2;
            }
            else if (r1 == r2)
            {
                cout << "NO" << endl;
                flag = 0;
                break;
            }
        }
        if (flag)
            cout << "YES" << endl;
    }
    return 0;
}

离散化

定义

离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。

通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。例如：

原数据：1, 999, 100000, 15；

处理后：1, 3, 4, 2；

原数据：{100, 200}，{20, 50000}，{1, 400}；

处理后：{3, 4}，{2, 6}，{1, 5}；

对于离散化来说主要有三个步骤

一.去重（用unique去重函数）

二.排序

三.二分索引（用lower_bound函数）

const int N = 1e5 + 7;

int t[N], a[N];

int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
           cin >> a[i];
        t[i] = a[i];
    } 
    sort(t + 1, t + n + 1);
    m = unique(t + 1, t + n + 1) - t - 1;
    for (int i = 1; i <= n; i++)
        a[i] = lower_bound(t + 1, t + m + 1, a[i]) - t;
}

在这段代码中，a[ ]经过离散，范围就变成了m。解释一下，unique是c++自带的一个函数，表示对一个数列去重，然后返回不重复的元素个数，当然在后面要减去首地址。那么这种离散化对于有重复元素的数列也可以适用，但是复杂度会高些。有一种离散化的方式复杂度会低一些，但是不能处理有重复元素的数列，所以在此不再赘述

举个例子：原数据：{6, 8, 4, 9, 5, 6, 7, 4}，首先排序后得到{4, 4, 5, 6, 6, 7, 8, 9}，去重{4, 5, 6, 7, 8, 9}，然后原序列就变成了{3, 5, 1, 6, 2, 3, 4, 1}。

lower_bound( )

这里是关于lower_bound( )和upper_bound( )的常见用法

lower_bound( )和upper_bound( )都是利用二分查找的方法在一个排好序的数组中进行查找的，这两个函数都需要加载头文件#include<algorithm>

在从小到大的排序数组中，

lower_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

upper_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

在从大到小的排序数组中，重载lower_bound()和upper_bound()

lower_bound( begin,end,num,greater<type>() ):从数组的begin位置到end-1位置二分查找第一个小于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

upper_bound( begin,end,num,greater<type>() ):从数组的begin位置到end-1位置二分查找第一个小于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
//#define DEBUG(x) cerr << #x << "=" << x << endl
#define LL long long
const int maxn = 1e5 + 10;
const int INF = 2 * int(1e9) + 10;

int cmd(int a, int b)
{
    return a > b;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int num[6] = {1, 2, 4, 7, 15, 34}; 
    sort(num, num + 6);                                             //按从小到大排序 
    int pos1 = lower_bound(num, num + 6, 7) - num;                    //返回数组中第一个大于或等于被查数的值 
    int pos2 = upper_bound(num, num + 6, 7) - num;                    //返回数组中第一个大于被查数的值
    cout << pos1 << " " << num[pos1] << endl;
    cout << pos2 << " " << num[pos2] << endl;
    sort(num, num + 6, cmd);                                           //按从大到小排序
    int pos3 = lower_bound(num, num + 6, 7, greater<int>()) - num;  //返回数组中第一个小于或等于被查数的值 
    int pos4 = upper_bound(num, num + 6, 7, greater<int>()) - num;  //返回数组中第一个小于被查数的值 
    cout << pos3 << " " << num[pos3] << endl;
    cout << pos4 << " " << num[pos4] << endl;
    return 0;    
}