数学：矩阵乘法加速

Codevs1281:

给你6个数，m, a, c, x0, n, g

Xn+1 = ( aXn + c ) mod m，求Xn

计算递推式，运用矩阵来进行计算加速

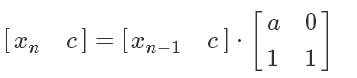
然后注意用类似快速幂的方法写一个快速加，避免溢出

怎么把式子化成矩阵，日后再补

#include<cstdio>
long long mod,a,c,x0,n,g;
struct Mat
{
    long long m[2][2];
}base,X0;
long long quick_add(long long a,long long b)
{
    long long ans=0;
    a%=mod;b%=mod;
    while(b>0)
    {
        if(b&1) ans=(ans+a)%mod;
        a=(a+a)%mod;
        b>>=1;
    }
    return ans;
}
Mat mul(Mat a,Mat b)
{
    Mat ans;
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
        {
            long long sum=0;
            for(int k=0;k<2;k++)
                sum=(sum+quick_add(a.m[i][k],b.m[k][j]))%mod;
            ans.m[i][j]=sum;
        }
    return ans;
}
Mat pow(Mat a,long long n)
{
    Mat p={{1,0,0,1}};
    while(n>0)
    {
        if(n&1) p=mul(p,a);
        a=mul(a,a);
        n/=2;
    }
    return p;
}
int main()
{
    scanf("%lld%lld%lld%lld%lld%lld",&mod,&a,&c,&x0,&n,&g);
    base=(Mat){{a,0,1,1}};
    X0=(Mat){{x0,c,0,0}};
    Mat ans=mul(X0,pow(base,n));
    printf("%lld
",ans.m[0][0]%g);
    return 0;
}