先上状态转移方程,还是很容易看明白的
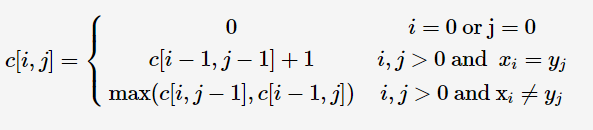
例题是Codevs的1862,这个题不是实现了方程就可以了的,还要完成一个事情那就是计数,数一数到底有多少个最长公共子序列
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int maxn=5005; 6 const int p=1e8; 7 char a[maxn],b[maxn]; 8 int dp[maxn][maxn],f[maxn][maxn]; 9 int main() 10 { 11 scanf("%s%s",a+1,b+1); 12 int al=strlen(a+1)-1; 13 int bl=strlen(b+1)-1; 14 for(int i=0;i<=al;i++) f[i][0]=1; 15 for(int i=0;i<=bl;i++) f[0][i]=1; 16 for(int i=1;i<=al;i++) 17 for(int j=1;j<=bl;j++) 18 { 19 if(a[i]==b[j]) 20 { 21 dp[i][j]=dp[i-1][j-1]+1; 22 int k1=0,k2=0; 23 if(dp[i][j]==dp[i-1][j]) k1=1; 24 if(dp[i][j]==dp[i][j-1]) k2=1; 25 f[i][j]=f[i-1][j-1]+(k1*f[i-1][j])+(k2*f[i][j-1]); 26 f[i][j]=(f[i][j]+p)%p; 27 } 28 else 29 { 30 dp[i][j]=max(dp[i-1][j],dp[i][j-1]); 31 int k1=0,k2=0,k3=0; 32 if(dp[i][j]==dp[i-1][j]) k1=1; 33 if(dp[i][j]==dp[i][j-1]) k2=1; 34 if(dp[i][j]==dp[i-1][j-1]) k3=1; 35 f[i][j]=(k1*f[i-1][j])+(k2*f[i][j-1])-(k3*f[i-1][j-1]); 36 f[i][j]=(f[i][j]+p)%p; 37 } 38 } 39 printf("%d %d ",dp[al][bl],f[al][bl]); 40 return 0; 41 }
在这里我们用dp记录长度,用f记录个数
由于输入是以“.”结尾的,所以读入的时候有些许的变化
scanf("%s%s",a+1,b+1); int al=strlen(a+1)-1; int bl=strlen(b+1)-1;
这样读入的时候真正的字符串的下标是从a+1开始的,循环的时候从1开始循环,到strlen(a+1)结束
因为结尾字符不属于串,所以给al--就好了