树的表示方法
1 一般表示法

2 广义表表示法

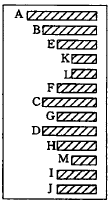
3 凹入表示法
树的基本术语:
树:n(n>=0)个结点的有限集
结点:包含一个数据元素及若干指向其子树的分支
结点的度:结点拥有的子树数成为结点的度
叶子(也叫终端结点):度为0的结点
非终端结点(也叫分支结点):度不为0的结点
树的度:树内各结点的度的最大值
孩子:结点的子树的根成为该结点的孩子
双亲:若B结点是A结点的孩子,则A结点是B结点的双亲
堂兄弟:其双亲在同一层的结点护卫堂兄弟
结点的层次:从根开始定义起,根为第一层,根的孩子为第二层
树的深度(也叫高度):树中结点的最大层次。
有序树:子树有序的树
无序树:不考虑子树的顺序
森林:m(m>=0)棵互不相交的树的集合。
二叉树定义
在二叉树中,每个结点至多只有两颗子树,并且,二叉树的子树有左右之分,其次序不能颠倒。关于树的术语也都适用于二叉树
完全二叉树定义
一颗深度为k,除第k层外,其它各层的结点数(1~k-1)的结点数都达到最大个数,第k层有叶子结点,且叶子结点从左至右依次排布,这就是完全二叉树。
满二叉树定义
一颗深度为k且有2k-1个结点的二叉树成为满二叉树
二叉树性质
性质1 在二叉树的第i层上至多有2i-1个结点
性质2 深度为k的二叉树至多有2k-1个结点, 用等比数列求和公式就可容易证明
性质3 对任何一颗二叉树T,终端结点数n0和度为2的结点数n2的关系如下:
n0=n2+1,在博客“内部排序->选择排序->树形选择排序”的附录1已经证明过。
性质4 具有n个结点的完全二叉树的深度为[log2n]+1
证明:假设深度为k, 根据性质2和完全二叉树的定义有
2k-1 < n <= 2k-1
性质5 对一颗有n个结点的完全二叉树,按层序编号,则对任一结点,都有:
(1) 根结点除外的其它结点i的双亲为[i/2]
(2) 结点i的左孩子结点为2*i,(2*i不超过树的结点个数的情况下)
(3) 结点i的右孩子结点为2*i+1, (2*i+1不超过树的结点个数的情况下)