常见的基本数据结构——栈

栈ADT

栈(stack)是限制插入和删除只能在一个位置上进行的表，该位置是表的末端，叫做栈顶。栈的基本操作有进栈(push)和出栈(pop)，前者相当于插入，后者相当于删除最后的元素。在最后插入的元素可以通过使用Top例程在执行Pop之前进行考查。对空栈进行的Pop或Top一般被认为是栈ADT的错误。另一方面，当运行Push时空间用尽是一种实现错误，但不是ADT的错误。

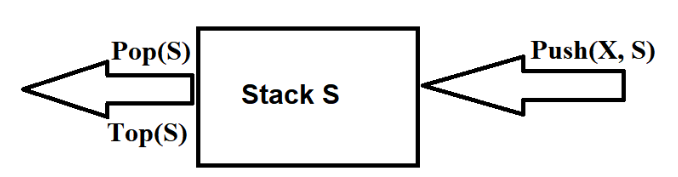
栈有时又叫做LIFO(后进先出表)。

栈的实现

由于栈是一个表，因此任何实现表的方法都能够实现栈。两种流行的方法：一种是使用指针实现，一种是使用数组实现。

栈的链表实现

在表的顶端插入实现Push，在表的顶端删除实现Pop，Top只是返回顶端元素，有时Top和Pop两个也可以合二为一。

栈ADT链表的声明实现

struct Node；
typedef struct Node *PtrTONode;
typedef PtrToNode Stack;

struct Node{
　　ElementType Node;
　　PtrToNode Next;
};

测试栈是否为空

int

IsEmpty(Stack S){

　　return S->Next == NULL;

}

创建一个空栈也很简单，我们只要建立一个头结点，MakeEmpty设置Next指针指向NULL。Push是作为向链表前端进行插入而实现的，其中，表的前端作为栈顶。Top的实现是返回表的前端的元素，Pop是通过删除表的前端元素实现。

创建一个空栈的过程

Stack
CreateStack(void){
　　Stack S;
　　S = malloc(sizeof(struct Node));
　　if(S == NULL){
　　　　printf(” out of space”);
　　}
　　S->Next == NULL;
　　MakeEmpty(S);
　　return S;
}


void 
MakeEmpty(Stack S){
　　if(S == NULL){
　　　　Error();
　　}else{
　　while(!IsEmpty(S)){
　　　　Pop(s);
　　}
}

Push进栈例程

void
Push(ElememtType X, Stack S){
　　PtrToNode TemCell;
　　TemCell = malloc(sizeof(struct Node));
　　if(TemCell == NULL){
　　　　Error();
　　}else{
　　　　TemCell->ElementType = X;
　　　　TemCell->Next = S->Next;
　　　　S->Next = TemCell;
　　}
}

Pop操作实现

ElementType
Top(Stack S){
　　if(!IsEmpty(S))
　　　　return S->Next->Element;
　　Error();
　　return 0;
}

对于链表的实现，所有的操作基本上都只花费常数的时间，上述的操作出了空栈之外都没有涉及到栈的大小，更没有依赖栈进行循环了。这种实现的缺点是对于malloc和free操作是昂贵的开销。有的缺点可以通过两个栈进行避免，第二个栈初始化为空栈，当单元弹出时，它只是被放入到第二个栈，此后当需要新空间时，首先检查第二个空栈。

栈的数组实现

数组实现避免了指针操作并且是更流行的实现，唯一的不足是它先要声明一个数组的大小。通常栈的实际个数并不会太大，声明一个合理的空间没有什么困难。如果不能的话，那就采用链表实现。数组实现栈是非常简单的，每一个栈都有一个TopOfStack，空栈时为-1，当某个元素压入栈时，将TopOfStack加1，然后至Stack[TopOfStack] = X;其中，Stack就是具体栈的数组。出栈时，我们返回Stack[TopOfStack]的值，然后TopOfStack减1，为了Stack和TopOfStack相对应，它们应该是栈结构的一部分。

上述的操作不仅以常数时间运行，而且是以非常快的时间运行。在现代化的计算机中，栈已经成为操作系统指令的一部分。一个影响栈执行效率的问题是错误检查。

栈的声明

struct StackRecord；
tepedef struct StructRecord * Stack;

struct StackRecord{
    int Capacity;
    int TopOfStack;
    int ElementType *Array;
}

Stack 
CreateStack(int MaxElement){
　　Stack S;
　　if(MaxElement < MinStackSize)
　　Error();
　　S = malloc(sizeof(struct StackRecord));
　　if(S == NULL)
　　　　Error();
　　S->Array = malloc(sizeof(ElementType) * MaxElement);
　　if(S->Array == NULL)
　　　　Error();
　　S->Capacity = MaxElements;
　　MakeEmpty(S);
　　return S;
}

检测栈是否为空

int 
IsEmpty(Stack S){
　　return S->TopOfStack == EmptyTOS;
}

创建一个空栈

void 
MakeEmpty(Stack S){
　　S->TopOfStack = EmptyTOS;
}

进栈操作

void
Push(ElementType S, Stack S){
　　if(IsFull(S))
　　　　Error();
　　else
　　　　S->Array[++S->TopOfStack] = X;
}

返回栈顶元素

ElementType
Top(Stack S){
　　if(!IsEmpty(S))
　　return S->Array[S->TopOfStack];
　　Error();
　　return 0;
}

从栈顶弹出元素

void
Pop(Stack S){
　　if(IsEmpty)
　　　　Error();
　　else
　　　　S-TopOfStack—;
}

将Top和Pop进行合并

ElementType
TopAndPop(Stack S){
　　if(!IsEmpty(S)){
　　　　return S->Array[S->TopOfStack]; 
　　}
　　Error();
　　return 0;
}

应用

平衡符号

编译器检查你的程序的语法错误，当时常常由于缺少一个符号造成上百行的错误。在这种情况下，就需要一个工具检验成对出现，每一个双符号都要有对应的符号，一个简单的算法就用到栈，如下描述：

做一个空栈。读入字符直到文件尾。如果字符是一个开放字符，则将其推入栈中，如果字符是一个封闭符号，则当栈空时报错。否则，将栈元素弹出，如果弹出的符号不是对应的开放符号，则报错。在文件尾，如果栈非空则报错。

上述的算法是线性的，事实上，它只要对输入进行一趟检验。因此，它是在线的，速度非常的快。

后缀表达式

在一个由优先级构成的算术表达式中，我们通常要根据运算符的有限级进行计算结果。请下面的例子：

4.99 + 5.99 + 6.99 * 1.06 = 18.69

如果没有考虑优先级的话，计算的结果将是19.37.我们可以通过下面的方法进行计算，操作顺序如下：

4.99 1.06 * 5.99 +6.99 1.06 * +

上面的记发叫做后缀或者逆波兰记法。计算这个问题最容易的办法就是使用一个栈：当遇见数时，就把它放入栈中，在遇到运算符时就作用于栈中弹出的两个数，并将结果推入栈中。

计算一个后缀表达式的时间是线性的O(N)，对输入的元素由一些栈操作组成从未花费常数的时间，并且不必要知道任何的有限顺序。

中缀到后缀的转换

栈不仅可以计算后缀表达式，而且还可以将一个标准的表达式(中缀表达式)转换成后缀表达式。如下中缀表达式：

a + b * c + (d * e + f) * g

转换成后缀表达式：

a b c * + d e * f + g * +

具体操作是：当读到一个操作数的时候，立即把它放到输出中，操作符不立即输出，保存在某个地方，正确的做法是将遇到的操作符保存在栈中，遇到左括号也放入栈中。

如果遇见一个右括号，那么就将栈元素弹出，将弹出的符号输出直到遇见相匹配的左括号，但是左括号不进行输出。

如果我们遇见任何其他的符号，那么我们从栈中弹出栈元素直到发现优先级更低的元素为止。有一个例外，除非是一个）的时候，否则我们绝不从栈中移除（。对于这种操作，+的优先级最低，（优先级最高。当弹出元素结束后，我们在将操作符移入栈中。

当到达末尾时，我们将栈中元素弹出，变成空栈，将符号输出。

同样，这种转换只需要O（N）的，对于运算符时是从左到右的结合的，上面的算法是正确的，不然就需要重新设计。

函数调用

当存在函数调用时，需要存储重要的信息，诸如寄存器的值，和返回的地址，都要以抽象的方式存在一张纸上并被置于一个堆的顶部。

递归的不当使用:打印一个链表

void
PrintList(List L){
　　if(L != NULL){
　　　　PrintElement(L->Element);
　　　　PrintList(L->Next);
　　}
}

这个程序是尾递归，是使用极端不当的例子，尾部涉及在最后一步的递归。

尾递归可以通过将递归调用变成goto语句并在其前加上对函数每个参数的赋值语句而手工删除。它模拟了递归调用，因为没有什么需要存储的值，在递归调用之后，实际上没有必要知道存储的值。下面是通过goto改造的while循环实现：

void 
PrintList(List L){
　　top:
　　if(L != NULL){
　　　　PrintElement(L->Element);
　　　　L = L->Next;
　　　　goto top;
　　}
}

递归总是能够彻底除去，但是有时是相当冗长复杂的。一般方法是使用一个栈来消除，虽然非递归确实比递归程序要快，但是速度的优势代价确实由于去除而使得程序的清晰度不足。