传统的递归实现
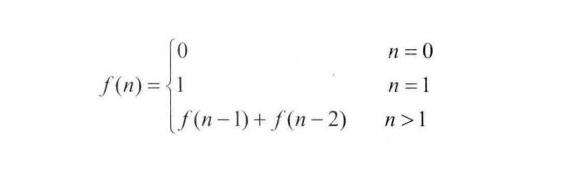
public long fibonacci(int n) {
if (n <= 0) {
return 0;
}
if (n == 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
但以递归求解的过程中会出现很多重复求解 如图:
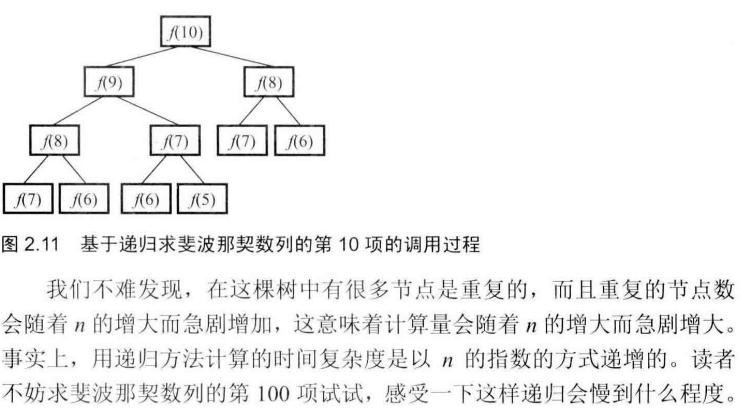
思路
优化方法:
- 把已得到的数列保存起来,下次计算时先查询,已计算过就不用重复计算.
- 采用从下往上计算,可以把计算过了的保存起来,下次要计算时就不必重复计算了:先由f(0)和f(1)计算f(2),再由f(1)和f(2)计算f(3)……以此类推就行了,计算第n个时,只要保存第n-1和第n-2项就可以了。
实现
public long fibonacci(int n) {
int result[] = {0, 1};
if (n < 2) {
return result[n];
}
long fibNMinusOne = 1;
long fibNMinusTwo = 0;
long fibN = 0;
for (int i = 2; i <= n; i++) {
fibN = fibNMinusOne + fibNMinusTwo;
fibNMinusTwo = fibNMinusOne;
fibNMinusOne = fibN;
}
return fibN;
}
变种I
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
思路
将跳法总数记为f(n),可以知道f(1)=1,f(2)=2。当n>2时,第一次跳1级的话,还有f(n-1)种跳法;第一次跳2级的话,还有f(n-2)种跳法,所以可以推得f(n)=f(n-1)+f(n-2).
实现
public int JumpFloorI(int n) {
if (n ==2) {
return 2;
}
if (n == 1) {
return 1;
}
return JumpFloorI(n - 1) + JumpFloorI(n - 2);
}
变种II
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
思路
n级台阶,第一步有n种跳法:跳1级、跳2级、到跳n级
跳1级,剩下n-1级,则剩下跳法是f(n-1)
跳2级,剩下n-2级,则剩下跳法是f(n-2)
所以f(n)=f(n-1)+f(n-2)+...+f(1)
因为f(n-1)=f(n-2)+f(n-3)+...+f(1)
两个相减f(n)-f(n-1)=f(n-1)
所以f(n)=2*f(n-1)
实现
public int JumpFloorII(int n) {
if (n == 1) {
return 1;
} else {
return 2 * JumpFloorII((n - 1));
}
}
变种III
我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。
请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
思路
- target= 1大矩形为2*1,只有一种摆放方法,return1;
- target= 2 大矩形为2*2,有两种摆放方法,return2;
- target= n时候第一次摆放有两种方式


因为,摆放了一块12的小矩阵,对应下方的12,摆放方法就确定了,所以为f(targte-2)
此解来自牛客网Follow
实现
public int RectCover(int target) {
if (target < 1) {
return 0;
}
if (target == 1) {
return 1;
}
if (target == 2) {
return 2;
}
return RectCover(target - 1) + RectCover(target - 2);
}