散列:原理
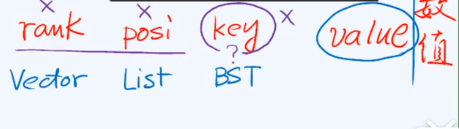
桶bucket:直接存放或间接指向一个词条(即词条的引用)
桶数组bucket array/散列表hash table,容量为M,即散列表长度
N < M << R
空间 = O(N+M)=O(N)
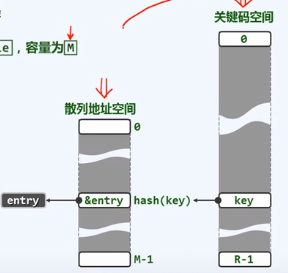
定址/杂凑/散列:
根据词条的key(未必可比较)
直接确定散列表入口
散列函数:hash(): key->&entry 将关键码转为词条或它的入口

电话簿
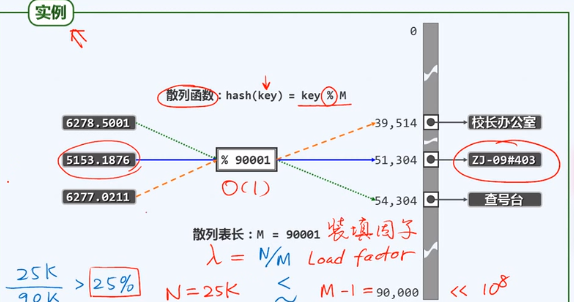
可能会出现冲突

二、散列:散列函数
无法杜绝的冲突
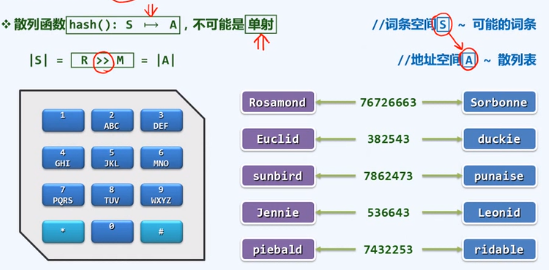
两项基本任务
近似的单射,往往可行

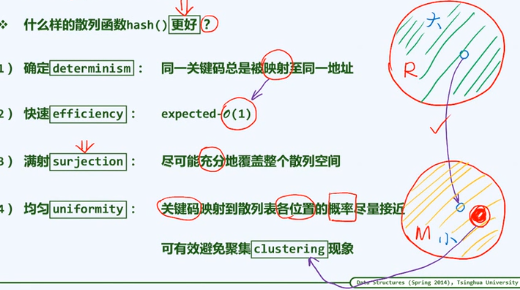
评价标准与设计原则
除余法

数据通常具有局部性Locality,典型的现象是数据序列中的数据项大多按某一步长单调变化(while、for)
如果数据序列的步长为S,S与M的最大公因子gcd(S, M)=G
当且仅当G=1时,数据序列的足迹能够遍布整个散列表

因为可能有不同的程序, 每个程序每次的运行对应的步长S未必相等,也就是说M相对于几乎任何S,最大公因子都只能是1。这意味着M是个素数。
MAD法
除余法的缺陷:
- 不动点:无论表长M取值如何,总有hash(0)=0
- 零阶均匀:[0, R)的关键码,平均分配至M个桶;但相邻关键码的散列地址也必相邻
一阶均匀:邻近的关键码,散列地址不再邻近
更高阶的均匀性呢?
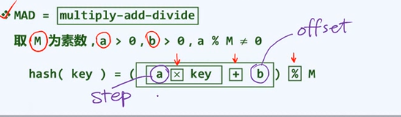
当然,特定场合下,未必需要高阶的均匀性
更多散列函数

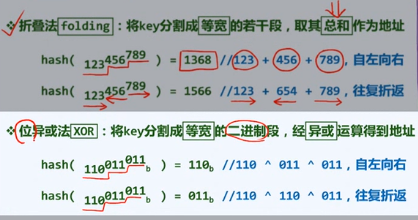
总之,越是随机越是没有规律越好
(伪)随机数法


多项式法

四、散列:排解冲突
事先预案
多槽位

独立链
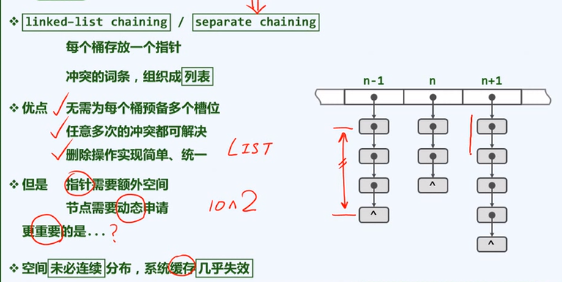
开放地址

线性试探
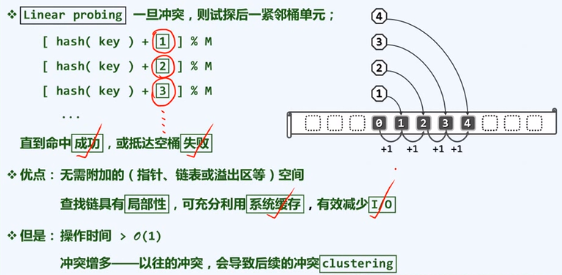
懒惰删除

平方试探
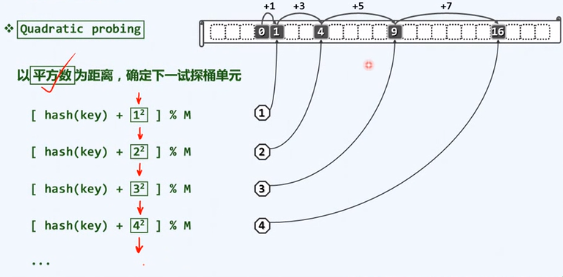
优点、缺点及疑惑
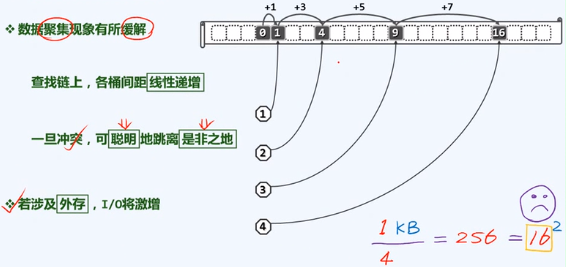
装填因子,须足够小
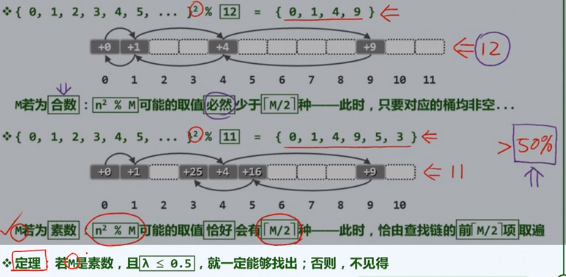
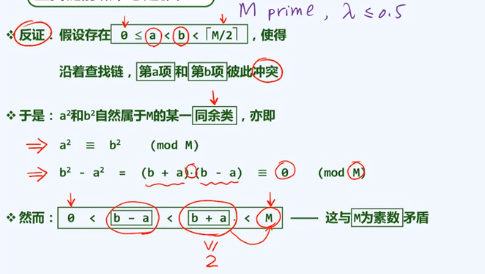
双向平方试探
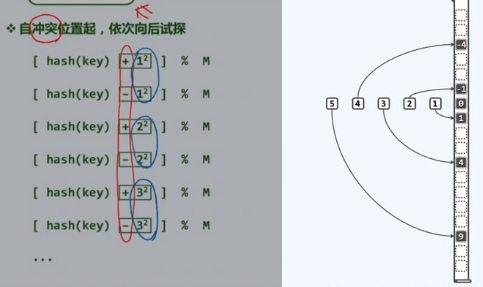
查找链,彼此独立?
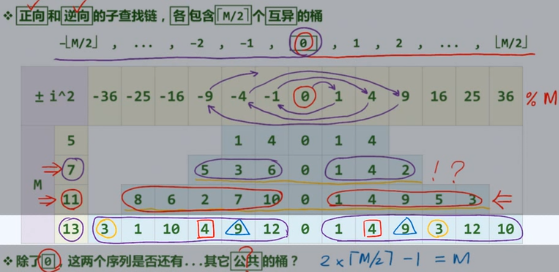
4k+3
双平方定理

五、桶/计数排序
