此篇 TensorFlow简要教程及线性回归算法示例 介绍了使用TensorFlow进行机器学习的基本流程,此篇 介绍一个快速确定神经网络模型中各层矩阵维度的方法 介绍了在设计神经网络的时候怎么确定各层矩阵的维度(矩阵的行数与列数),接下来就可以开始训练模型了,在训练模型的过程中,怎么衡量模型的好坏呢?通常用模型与真实之间的误差来表示,误差由 偏差 和 方差 两部分组成。
Bias(偏差)
模型在样本上的输出与真实值之间的误差,即模型本身的精准度,反应出算法的拟合能力。
Variance(方差)
模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性,反应出预测的波动情况。
偏差 与 方差 的关系
偏差与方差之间按照高低,可以组合成四种关系,如下图所示
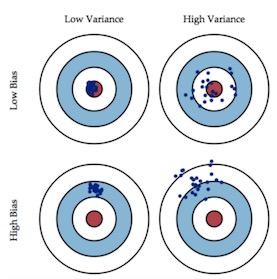
上图中 偏离 红色靶心 的蓝点 越多、越远,表示模型越差。
1、低偏差 低方差
表示模型既准确又稳定,效果最好,但是现实中这种情形很少遇见。
2、低偏差 高方差
表示模型准确但是稳定性差,对验证数据&测试数据的拟合能力差,即是模型的泛化能力差,产生了 过拟合(Overfitting)。
3、高偏差 低方差
表示模型的准确度差,对数据的拟合能力弱,产生了 欠拟合(Underfitting)。
4、高偏差 高方差
表示模型既不准确又不稳定。
过拟合 与 欠拟合
由上面的分析可知,高方差往往预示着过拟合,高偏差则是欠拟合。
避免欠拟合(拟合太差)
1、增加训练样本数据
2、设计更复杂的神经网络模型(加深、加宽等)
3、增加迭代次数
4、更好的优化函数
5、调整超参数值
避免过拟合(拟合过度,泛化太差)
1、设计更简单的神经网络模型
2、增加训练样本数据
3、正则化。在损失函数后面添加L2正则项
4、使用dropout。dropout的作用是随机地使得网络中的部分神经元失效,效果上类似将模型变得更简单。
5、调整超参数值
6、尝试其他模型
7、提前结束训练(early stopping)。即是提前结束优化损失函数。
简单小结
在实际的模型训练中,通常可以按下面的来操作
贝叶斯(最优)误差:理论上的最小误差值(通常比人类误差小)
可避免偏差:训练误差 与 贝叶斯误差 之间的差值
方差:验证集误差 与 训练误差 的差值
当 可避免偏差 大于 方差 时,发生 欠拟合。
当 方差 大于 可避免偏差 时,发生 过拟合。
在训练模型时对照以上描述,有助于定位问题,采取对应的措施调整模型,更快训练出最适合的模型。