0、模型选择
对于不同的业务场景,需要不同的策略来处理问题。没有一个算法可以处理好所有问题,并取得最好的效果。这样就是没有免费午餐原理。
因此,对于不同业务,不同的应用场景,需要选择不同的模型来解决实际问题。
对于模型的选择,可以分为两个层面:
1、对于一个既定算法,如何让这个算法达到最优?
2、对于不同的算法,如何评价不同算法的表现?
这两个层面的问题,本质都是要建立对于模型的评估标准,以标准客观评估模型。
一般来说,单一模型/算法的评估指标可以等同于其优化目标,也就是以优化目标为指标,算法优化得友好,指标越好(一点个人见解)。
但是这里存在两个问题:
1、模型空间和应用空间并不完全一致,模型的优化目标也就没有办法对应到应用上(比如点击率预估问题和LR的最大似然损失);
2、不同的算法可能采用不一样的目标,那么不同算法的优化结果并不直接可比。
基于以上问题,需要选择一个一个公允的评价指标,既可以反映应用问题的客观需求,也可以度量不同算法的效果。
接下来,我们就分别从这两个层面的评价指标展开。
既定算法层面的指标:损失函数。
不同算法的评价指标:召回率、准确率、AUC、MAP、NDCG等。
1、损失函数和参数估计
从评价指标的角度来说,损失函数是一个算法的评价指标。从机器学习的结构来说,机器学习包含三个部分: 模型、策略和算法。其中模型是对数据的刻画,策略是模型选择的依据——也就是确定用什么样的准则选择模型,算法是实现策略的途径。
在监督学习里面,策略的选择公共是通过损失函数来确定的,对给定模型,选择一个损失函数,然后通过算法求得损失函数最小的模型。
损失函数的确定,带有较强的主观性和实践性,可以通过多次尝试和实践,选择好的损失函数。同时对于分布已知的数据集,可以通过参数估计推导出合理的损失函数。
1.1、四个损失函数
不同的损失函数适用场景不一样。和具体模型搭配适用的效果也不一样。理论上说,模型和损失函数,可以有多种组合。但是对于一些特定算法,选择相应的损失函数较为适宜。列举四个损失函数如下:
1)平方损失:最为常见的损失函数,形式如下
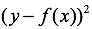
2)合页损失:SVM的损失函数,形式如下

3) 逻辑斯蒂损失:逻辑回归、最大熵模型的损失函数,形式如下

4)指数损失:AdaBoost的损失函数,形式如下
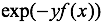
1.2、参数估计
对于已知分布的模型,给定一组分布参数就可以确定模型。通过参数估计,可以确定分布的参数。参数估计包括点估计和区间估计(这里只说点估计)。
常见的点估计方法包括:最大似然估计(MLE),最大后验估计(MAP)
1.2.1、最大似然估计(MLE,Maximum likelihood estimation)
最大似然估计的前提是数据是独立同分布的。假设数据分布的样本是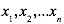 ,参数是
,参数是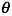 ,模型为
,模型为 。那么对于此参数分布产生的数据的似然函数为:
。那么对于此参数分布产生的数据的似然函数为:
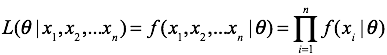
其对数似然为:

其最大对数似然估计为:
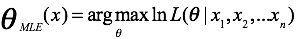
以以上估计函数为优化目标,就可以得出分布的参数。
最大熵就是一种MLE。参考:最大熵模型。
最小二乘估计同样是一种MLE,具体地说,是误差符合标准正太分布的线性模型的MLE。参考: https://www.zhihu.com/question/20447622/answer/25186207,最大似然估计和最小二乘法怎么理解
1.2.2、最大后验估计(MAP,Maximum a posteriori estimation)
最大似然估计的一个潜在问题是过拟合,尤其是在数据量少的时候。原因在于最大似然估计的目标是使得样本产生的概率最大,并不没有考虑分布参数的一些性质。
最大后验估计就是一种可以把分布参数的先验知识考虑进来的估计方法。
沿用上面的记号,并假设参数的先验分布函数为g,则根据贝叶斯公式有,参数的后验分布为:
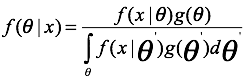
最大后验函数为:
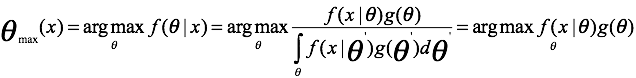
从公式中容易看到,与最大似然估计不同,最大后验估计使用了先验信息。
2、模型评估
接下来说一下模型评估中的评估指标、如何评估以及模型泛化问题。
2.1、评估指标
2.1.1、分类问题指标
1)混淆矩阵
分类问题的指标及其相关术语都离不开混淆矩阵。所谓混淆矩阵,就是真实的样本分类和预估的样本分类构成的矩阵:比如用不同的列,表示不同的真实的样本分类,用行表示预估的样本分类。以二分类问题为例,其混淆矩阵及相关的定义如下:
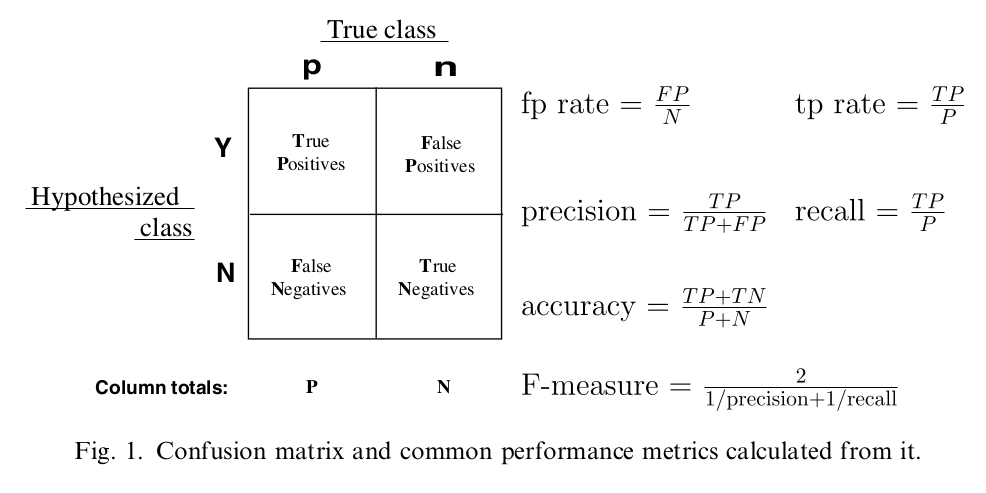
上图中,预估的正样本叫做Positive,负样本叫做Negative。真实的正样本,预估也为正样本,叫做True Positive;负样本预估为正样本,叫做False Positive。类似的可以定义False Negative和True Negative。分别简写为: TP、FP、FN、TN。又定义P=TP+FP,N=FN+TN。
2)准确率
准确率(Accuracy)表示所有样本分类正确的比例,包括正样本分类正确和负样本分类正确。定义:accuracy=(TP+TN)/(P+N)。
准确率可以用来度量分类器的分类效果,但它并不总是能有效的评价一个分类器的工作。举个例子:数据集中有100, 000, 000个样本,其中100个正样本,其余为负样本。那么我只需要将所有样本都预估为负样本,则accuracy为99.9999%,准确率极高,但是显然,这种预估结果不是我想要的。
3)准确率(Precision,IR中叫查准率)、召回率(Recall,IR中叫查全率)、PRC、F-Score
准确率的公式为Precision = TP/ (TP+FP)。表示预估为正的样本中真实正样本的比例。召回率的公式Recall = TP/(TP+FN)。表示真实正样本,被预估为正样本的概率。
简单思考可以发现,准确率和召回率是一对有矛盾的指标——为了提升召回率,把更多的样本预估为正样本,则引入的假正样本也会增加,准确率可能降低;同样地,为了提升准确率,提升预估为正的样本的门槛,召回量减小,召回率可能降低。也正是这样的矛盾,解决了前面准确率遇到的问题。
在很多情形下,我们可以更加学习器的预测效果对样本进行排序,排在前面的是最可能的正样本,排在第二位是是次可能的正样本。按此顺序,可以从第一位开始,逐次将排在自己前面的样本作为正样本进行计算,分别得到一系列的准确率、召回率,从而可以得到一条准确率-召回率曲线(P-R curve,也就是PRC)。如下图:

每一条PRC下面的面积,就可以作为模型好坏的评估指标。但是PRC曲线下面积不容易计算,此时可以以F-score可以作为PRC的近似指标。
F-score定义如下:
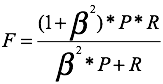
其中,P、R分别表示准确率和召回率。F是P、R的加权调和平均。 是P、R的权重调和系数,当
是P、R的权重调和系数,当 =1时得到的F-Score又叫F1-Score。
=1时得到的F-Score又叫F1-Score。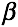 的不同取值,代表了在不同应用中准确率、召回率的不同重要程度。在推荐问题中,希望推荐尽可能精确,那么此时P较为重要,可以选择
的不同取值,代表了在不同应用中准确率、召回率的不同重要程度。在推荐问题中,希望推荐尽可能精确,那么此时P较为重要,可以选择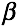 <1;在逃犯检测系统中,希望尽量少遗漏逃犯,此时R较为重要,可以选择
<1;在逃犯检测系统中,希望尽量少遗漏逃犯,此时R较为重要,可以选择 >1。
>1。
4)ROC曲线和AUC
ROC曲线全称receiver operating characteristic curve。其横坐标是FPR,纵坐标是TPR。其中TPR=TP/(TP+FN)=TP/P, FPR=FP/(FP+TN)=FP/N。分别表示正负样本预估为正的比例。类型PRC,可以通过排序和按排序预估,计算出一系列的TPR、FRR。将这点连连接起来就得到了ROC曲线。如下图:
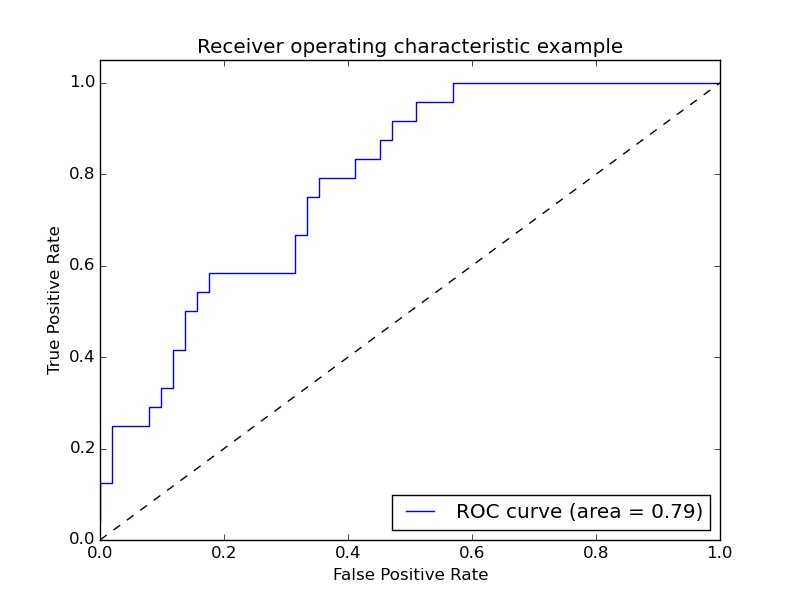
类似PRC曲线,ROC曲线下面积也可以度量分类器的性能。一般把ROC的曲线下面积叫做AUC(Area Under Curve)。
AUC的计算方式
与PRC的曲线面积难以计算不同,ROC的AUC有一种简单计算方法。假设正负样本数为M、N。首先对预估值从大到小排序,然后令最大预估值对应的样本的排序为n,第二大的排序为n-1,以此类推。然后把所有的正类样本的排序相加,再减去M-1种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的预估值大于负类样本的预估值。然后再除以M×N。即:
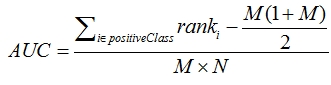
Tips:
PRC和ROC的比较
1) 对于PRC曲线,Recall和Precision的变化不是同步的,也就是说当Recall增大时,Precision可能增加/不变/降低(上面的PRC曲线中就可以看出)。曲线可能出现锯齿。ROC不存在这样的问题。
2)对于数据不平衡问题,PRC曲线更加敏感,ROC曲线相对更加稳定。如下图:

上图中,ac为ROC曲线;bd为PRC曲线;ab数据正负样本为1:1,cd数据样本比例为1:10。可以看出,在数据比例变化时,PRC曲线更加敏感,区分能力更强。
AUC的改进
在计算AUC时,不同的样本本身的预估区间范围有区别。比如对于不同流量上的数据,其预估值可能并不可比。但是在AUC计算时,把所有样本分到一起排序,掩盖了这一事实。改进的AUC算法主要是从此出发,把不同的样本分组,分别计算其AUC,然后进行加权。目前见到的,阿里妈妈的叫GUAC,头条的叫UAUC(按用户分组样本)。
5)代价曲线
在不平衡问题中,还有一类评估方法:代价曲线。
2.1.2、排序问题
两个最受欢迎的排名指标是MAP和NDCG。我们在前段时间已经使用了平均精度均值(MAP)。NDCG表示归一化折损累积增益。两者之间的主要区别是,MAP认为是二元相关性(一个项是感兴趣的或者不感兴趣的),而NDCG允许以实数形式进行相关性打分。
1)平均正确率(MAP, Mean Average Precision)
单个主题的平均准确率是每篇相关文档检索出后的准确率的平均值。主集合的平均准确率(MAP)是每个主题的平均准确率的平均值。MAP 是反映系统在全部相关文档上性能的单值指标。系统检索出来的相关文档越靠前(rank 越高),MAP就可能越高。如果系统没有返回相关文档,则准确率默认为0。
例如:假设有两个主题,主题1有4个相关网页,主题2有5个相关网页。某系统对于主题1检索出4个相关网页,其rank分别为1, 2, 4, 7;对于主题2检索出3个相关网页,其rank分别为1,3,5。对于主题1,平均准确率为(1/1+2/2+3/4+4/7)/4=0.83。对于主题2,平均准确率为(1/1+2/3+3/5+0+0)/5=0.45。则MAP= (0.83+0.45)/2=0.64。
2)归一化折扣累积增益(NDCG, Normalized Discounted Cumulative Gain)
NDCG的计算公式如下图所示:
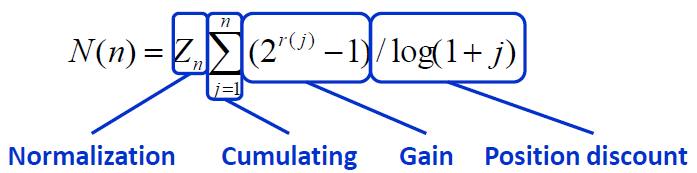
在MAP中,四个文档和query要么相关,要么不相关,也就是相关度非0即1。NDCG中改进了下,相关度分成从0到r的r+1的等级(r可设定)。当取r=5时,等级设定如下图所示:

(应该还有r=1那一级,原文档有误,不过这里不影响理解)
例如现在有一个query={abc},返回下图左列的Ranked List(URL),当假设用户的选择与排序结果无关(即每一级都等概率被选中),则生成的累计增益值如下图最右列所示:

考虑到一般情况下用户会优先点选排在前面的搜索结果,所以应该引入一个折算因子(discounting factor): log(2)/log(1+rank)。这时将获得DCG值(Discounted Cumulative Gain)如下如所示:

最后,为了使不同等级上的搜索结果的得分值容易比较,需要将DCG值归一化的到NDCG值。操作如下图所示,首先计算理想返回结果List的DCG值:
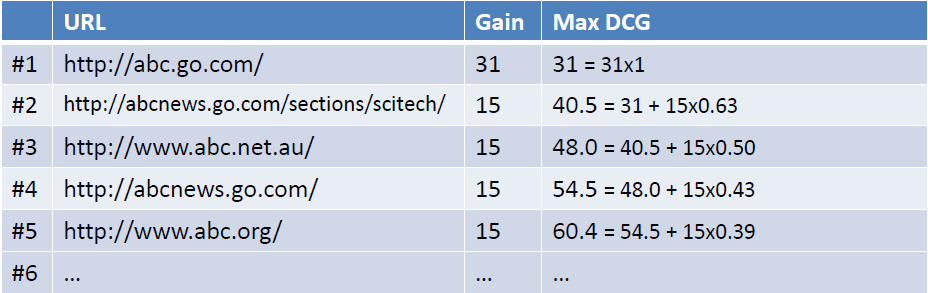
然后用DCG/MaxDCG就得到NDCG值,如下图所示:

2.2、模型检验
确定了模型算法和评价指标以后,需要在数据集合上运行算法,计算相关指标,从而评估和检验模型效果。这里对效果的评估依赖于两个集合,一个训练集,一个测试集。在训练集合上训练模型,在测试集合上评估模型效果。不同的集合划分划分就对应着不同的检验方法。
2.2.1、Hold-Out检验
Hold-Out方法是把数据集合划分为两个互斥的集合,一个作为训练集,一个作为测试集。以测试集上的误差作为模型的选择标准。
2.2.2、K-fold交叉验证
Hold-Out方法只对数据集合进行一次拆分,可能会改变数据分布,引入数据切分带来的误差。这一问题的解决方法是,对数据集进行多次切分。然后将多次评估的结果予以综合,得出最终的结论。这就是交叉验证的思想。
在交叉验证中,最为常见的方法是K-fold交叉验证。K-fold交叉验证,是讲数据集划分为k个大小相似的互斥子集。并且尽量保持每个集合数据分布与原数据集合一致。
然后每次选择其中一个集合作为测试集,其余集合作为训练集。进行K次训练和测试,最后的得出的结果是K次的均值。
使用交叉验证进行模型选择
2.2.3、自助法
在数据集合较小时,将数据集K等分,这样数据训练集合比原始数据集合小,可能因为数据不足而引起误差。此时可以通过自助法解决这一问题。
从原始数据D中,有放回地采样m个样本(其中m表示D中样本个数),得到集合D'。此时,未被采到的样本哪个概率是:

也就是D中大约有36.8%的没有被采样到,以未采样到的样本集合为测试集,以D'为训练集。进而评估模型效果。
Tips:
1)自助法在数据集合小,数据集合难以拆分时比较有效;
2)自助法可以从数据集合从产生多个不同数据集合,对于集成学习方法很有好处;
3)强化学习中也可以通过自助法采样来增加样本。
2.3、泛化能力分析
2.3.1、泛化性能
上面说到了在模型评估的时候需要把数据拆分成训练集和测试集。训练集合上的误差,表示的是模型对于已知数据的刻画;测试集合上的误差,表示的是在未知数据集合上,模型的效果。泛化误差表达了模型在未来实际应用中的效果。
2.3.2、过拟合、结构风险最小化、正则
过拟合
模型关于数据集合的平均损失成为经验风险。经验风险在样本不足的情况下,可能会让模型过度拟合到训练数据上,而在测试数据集上表现不好,这就是过拟合问题。
结构风险最小化和奥卡姆剃刀原则
为了防止过拟合现象,可以引入结构风险最小化,通过精简模型的结构,降低过拟合风险。在所有效果相当的模型中选择最简单的模型,这就是奥卡姆剃刀原则。
正则: L1/L2/ElasticNet
结构风险最小化,可以通过在损失函数中加入模型参数的范数来实现,这种方法也叫做正则化。如果加入的是1范数,则称为L1正则;如果加入的是2范数,则称为L2正则。
L1正则可以增加模型的稀疏性,减少特征数量;L2正则可以降低不同特征的影响,平滑特征权重。L1和L2正则相结合,就可以得到ElasticNet。
2.3.3、偏差方差分析
偏差和方差
模型的误差来源于三个方面:
1、模型对于真实数据的刻画能力,模型刻画能力和真实数据之间的差异,这就是偏差;表现就是模型不正确;
2、模型使用的数据和真实数据之间的关系,模型使用数据分布越接近真实分布,误差越小,训练数据的变化带来的模型扰动,就是方差;表现就是模型不稳定,泛化效果差;
3、数据本身存在的不确定性,也是就模型可以达到的误差的下界,就是噪声,这是数据本身学习的难度。
如果把打把看做一个机器学习问题,把把心当做真实数据的标注,把打把的环数当做训练数据,则打把的偏差和方差可以由下图来说明:
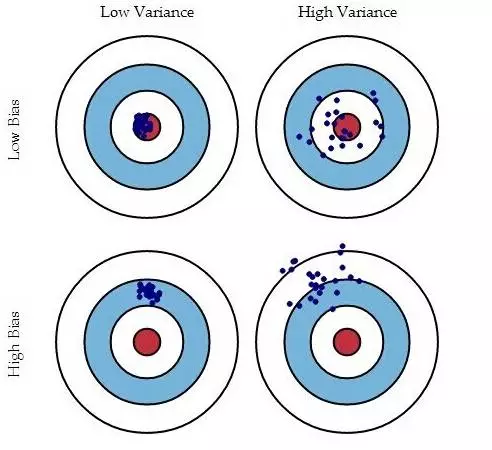
偏差和方差是有冲突的。当学习不足时,模型不准确,偏差高,不同数据集带来的扰动小,方差小;当学习过多时,模型过分拟合数据,造成过拟合,此时偏差低,但是在新数据集上的泛化能力差,方差大。如下图:
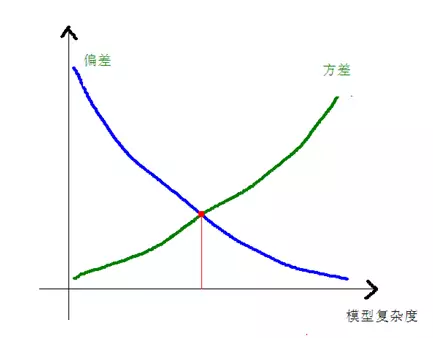
偏差方差和模型集成
对于模型集成的Bagging和Boosting方案来说:
Bagging用多个决策器做平均。单个决策器偏差较大时,会被多个决策器平均掉,造成的偏差较小;同时,多个决策器对于不同数据集做训练,其泛化性能较好,方差低。
Boosting提升的方法通过构造一系列的决策器对相同的训练数据集的重要性区别对待达到对训练数据的精确拟合,降低了偏差。
如果发现文中有问题,敬请联系作者批评指正,真诚欢迎您的指教,谢谢!
微信: legelsr0808
邮箱: legelsr0808@163.com