Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
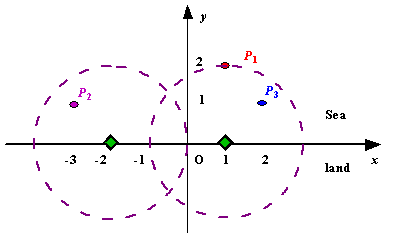
Figure A Sample Input of Radar Installations
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
/*********************************************************************************************************************** 题意:有n个岛屿和雷达覆盖半径d 求出要覆盖这些岛屿最少需要多少雷达 思路:把每个岛屿想象成一个雷达中心 则在岸边的覆盖区间可以写出 根据区间是否重叠来求出需要多少雷达 ***********************************************************************************************************************/ #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <queue> #include <stack> #include <vector> using namespace std; typedef struct { double l, r; }node; node a[1000+10]; bool cmp(node a , node b) { return a.l < b.l; } int main() { //freopen("data.in" , "r" , stdin); int n , d , cas = 0; while(scanf("%d %d", &n , &d) && (n || d)) { bool run = true; for(int i = 0 ; i < n ; i ++) { int tx, ty; scanf("%d %d", &tx, &ty); if(abs(ty) > d) run = false; a[i].l = (double)tx - sqrt((double)(d * d - ty * ty)); a[i].r = (double)tx + sqrt((double)(d * d - ty * ty)); } if(!run) { printf("Case %d: -1 " , ++cas); continue; } sort(a , a + n , cmp); int ans = 1; double last = a[0].r; for(int i = 1 ; i < n ; i ++) { if(a[i].l > last) { ans ++; last = a[i].r; } else if (a[i].r < last) last = a[i].r; } printf("Case %d: %d " , ++cas , ans); } return 0; }