Educational Codeforces Round 103 (Rated for Div. 2) A.K-divisible Sum+B.Inflation+C.Longest Simple Cycle题解

A. K-divisible Sum

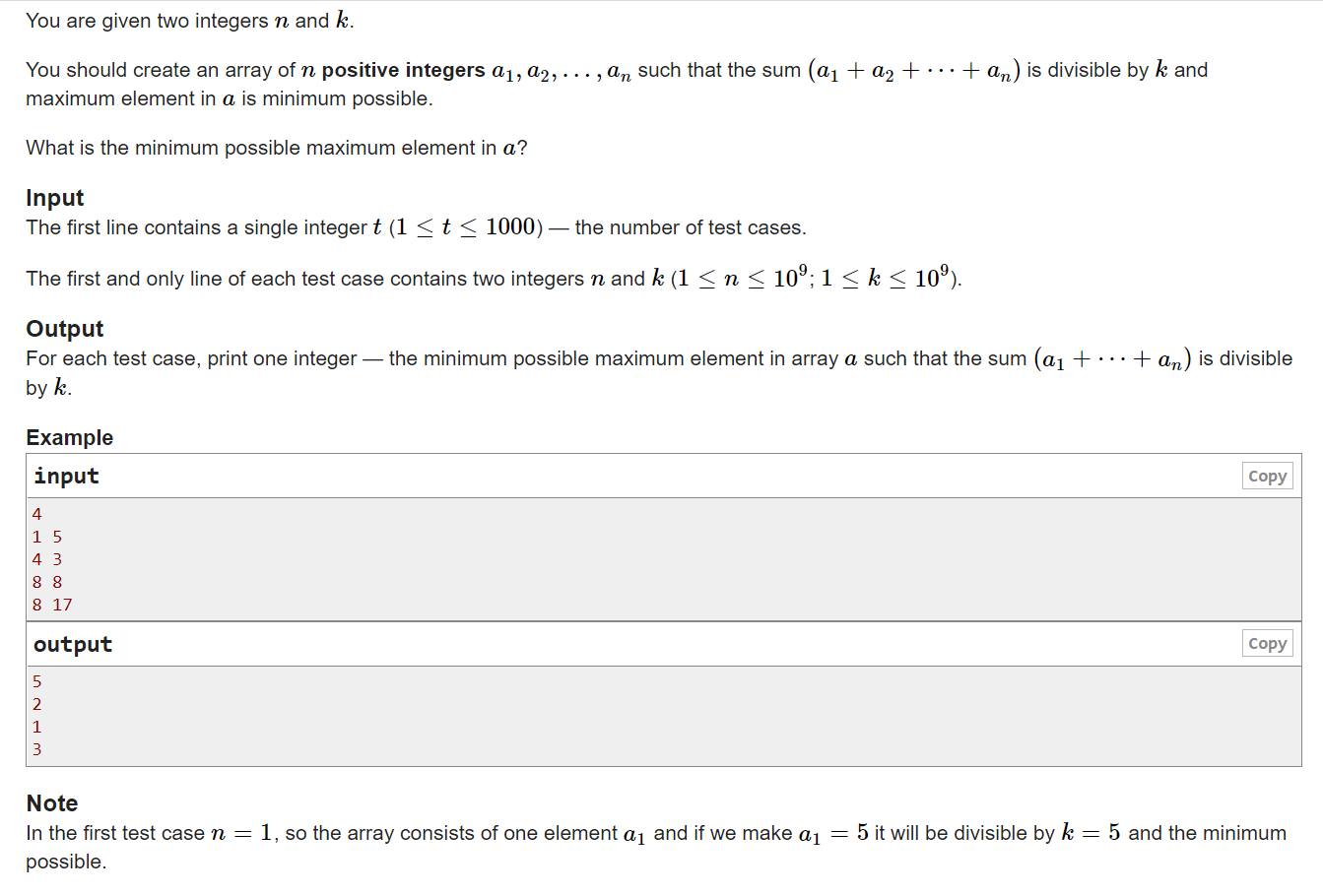
 题意：给两个数字n,k，构造一个有n个数的数组使得数组的总和可以整除k，且要使这个数组中的每个数尽可能的小，输出数组中的最大值；

思路：这题分两种情况

       一：k<=n ；这种情况也分为两种；

                   1.是n%k==0,这个时候数组中的数字都为1就可以整除k所以直接输出1;

                   2 当n%k！=0的时候，数组中的元素可以由若干个1和若干个2组成，所以输出2；

      二：k>n:这种情况就需要求一下；用k/n向上取整就是答案了

注意：第二种情况用循环会被hank tle,用ceil会因为输出类型被hank wa;//死伤惨重

#include <bits/stdc++.h>
#define  int long long
#define IOS ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0)
const int maxn=2e5+50;
const int INF=0x3f3f3f3f;
using namespace std;
int a[106][106];
int f[106][106];
signed main(){
  int t;cin>>t;
  while(t--){
      int n,k;
      cin>>n>>k;
     if(n<=k)
        cout<<(k+n-1)/n<<'
';//这样可以向上取整
        else{
        int    ans=n%k?2:1;
        cout<<ans<<'
';
      }
  }
  return 0;
}

B. Inflation

 

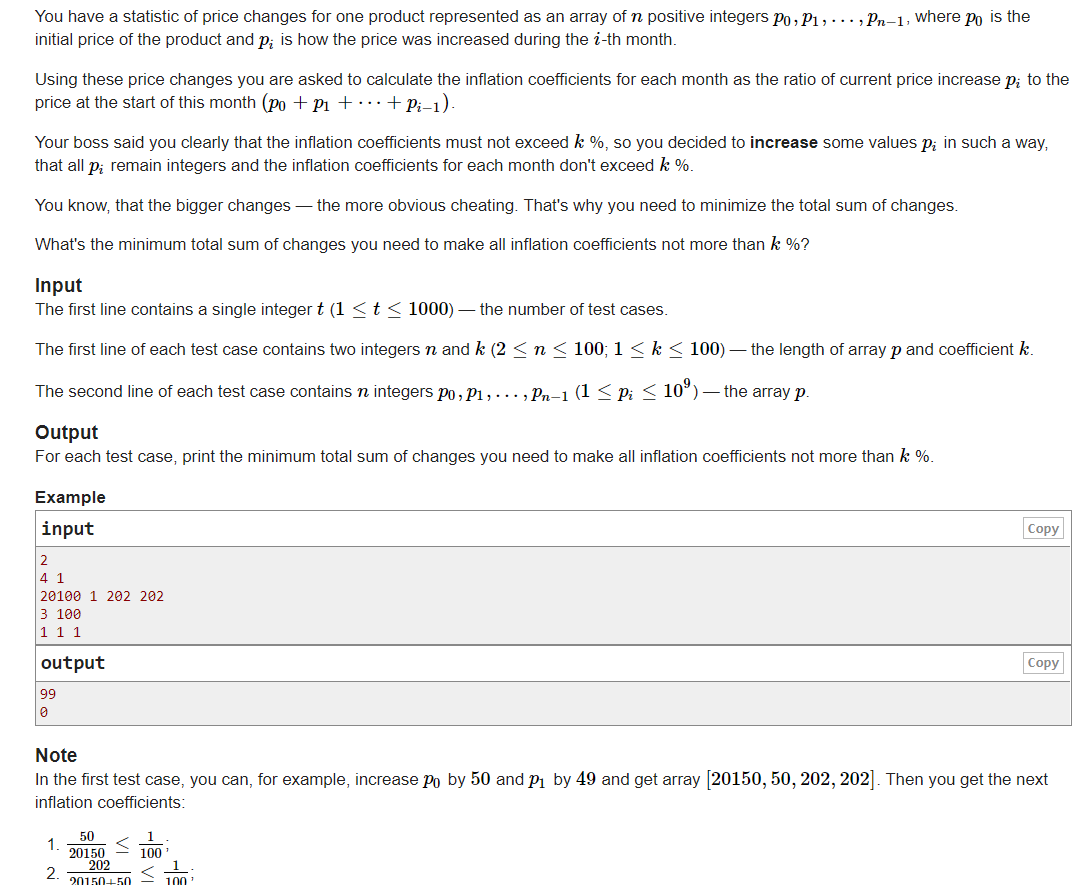
把所有的加到第一个上就好了

#include <bits/stdc++.h>
#define  int long long
#define IOS ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0)
const int maxn=2e5+50;
const int INF=0x3f3f3f3f;
using namespace std;
int a[maxn];
int f[106][106];
signed main(){
    IOS;
  int t;cin>>t;
  while(t--){
      double n,k;
      cin>>n>>k;
      for(int i=0;i<n;i++)cin>>a[i];
      int sum=a[0];
      int  ans=0;
      for(int i=1;i<n;i++){
          if(a[i]*100/k>sum){
              double t;
             t=ceil(a[i]*100/k);
             t-=sum;
              ans+=t;
              sum+=t;
           }
          sum+=a[i];
      }
      cout<<ans<<endl;
  }
  return 0;
}

C. Longest Simple Cycle

        

                  

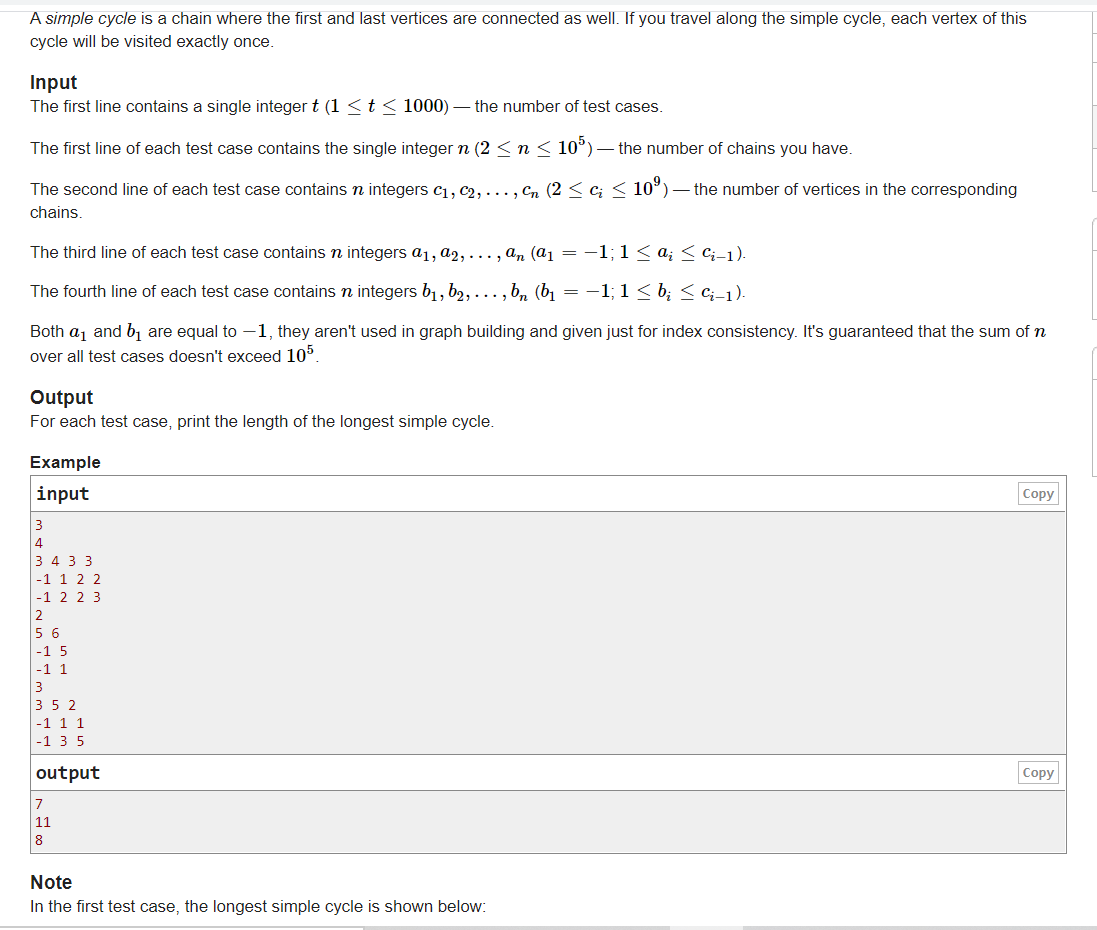
             题意：先给一个数字n，后面三行分别为n个绳子的长度，最上面的点连接前一个的第几个点，最下面的绳子连接上一个的点，求最大回路，

    我是采用动态规划，记录每一条绳子的最大回路的数据，然后实时更新最大值；

#include <bits/stdc++.h>
#define  int long long
#define IOS ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0)
const int maxn=2e6+50;
const int INF=0x3f3f3f3f;
using namespace std;
int c[maxn];
int a[maxn];
int  b[maxn];
int f[maxn];
signed main(){
    IOS;
  int t;cin>>t;
  while(t--){
     int n;cin>>n;
     for(int i=0;i<n;i++)cin>>c[i];
     for(int i=0;i<n;i++)cin>>a[i];
     for(int i=0;i<n;i++)cin>>b[i];
     f[0]=0;
     int ans=-1;
     for(int i=1;i<n;i++){
       if(a[i]==b[i]){f[i]=c[i]+1;
           ans=max(ans,f[i]);
       }
       else {
           f[i]=max(f[i-1]-abs(a[i]-b[i]),abs(a[i]-b[i]))+2+c[i]-1;
//f[i-1]-abs(a[i]-b[i])+2+c[i]-1是如果和前面一个联通的值，abs(a[i]-b[i])+2+c[i]-1是不和前面联通的值，两值求最大就好了；
           ans=max(ans,f[i]);
           
       }//cout<<f[i]<<" ";
     }
     cout<<ans<<'
';
  }
  return 0;
}