思路:搜索+剪枝。
本人在撰写这篇题解之前,在网络上搜索过别的题解,发现仅此一篇题解。在学习理解该题解的基础上编写了此题的代码,因此思路上很相像。以下为自己理解的内容,请放心食用。
首先,审题之后,我们可以发现山羊的移动就是从 ((x,y,z)) 到 ((xpm1,y,z)) ((x,ypm1,z)) ((x,y,zpm1)) 。这是典型的三维迷宫问题,数据范围 (1500 approx 11 imes 11 imes 12),肯定用搜索来解决。
在这个题中,我们考虑直接枚举战舰放置的位置。如果我们枚举一对点,这两个点能同时放置上战舰,有两种情况:
- 这两艘战舰互不影响。
- 这两艘战舰扩展出的地方接壤。
对于第一种情况,考虑放置战舰的点所在的联通块,如果两个联通块没有交界,显然满足互不影响的条件。
对于第二种情况,可以画图理解。
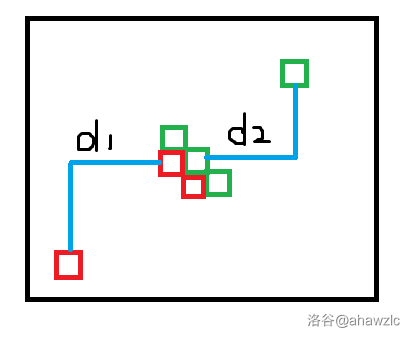
上图举了一个二维的平面为例。
显然有一个结论,如果两个联通块有交界,记交界处的点与战舰所在位置的曼哈顿距离分别为 (d1,d2) ,则有 (d1=d2) 或者 (d1=d2+1) 。否则该位置一定不可能出现交界。
很显然这是一个剪枝,记做剪枝 1 。
所以我们可以根据这个条件,先预处理出选取每个点会导致哪些点不能选。
还有另外两个常见的剪枝。
剪枝 2 是如果当前点被选中后,会导致某个颜色的战舰无法被安放,直接回溯。显然这种情况下怎么搜也搜不到解。
剪枝 3 是搜索限制条件多的点,这个可以处理出来。
同时,在看到数据范围是积的形式后,肯定需要把三维点转化成一维的点。
Code:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
const int NN=1503;
inline int read() {
int sum=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
sum=(sum<<3)+(sum<<1)+ch-'0';
ch=getchar();
}
return sum*w;
}
inline int get_c() {
char ch=getchar();
while(ch<'a'||'z'<ch) ch=getchar();
return ch-'a';
}
const int dx[6]={-1,1,0,0,0,0},dy[6]={0,0,-1,1,0,0},dz[6]={0,0,0,0,-1,1};//移动方向
int n,m,k,col,tot,rk[NN],pos[NN],siz[26],tmp[NN],res[26];
//col表示颜色总数,tot是将三维点转化为一维点后的点数
//rk表示点限制数目的排名,pos是rk的逆数组,tmp是点被访问的次数
//siz表示该颜色里点的数量,res表示该颜色剩余未访问的点的数量
int c[NN];//点的颜色
int s[26],top;//存储答案的栈
vector<int> v[NN];//限制
int cnt,h[NN*NN],nxt[NN*NN],to[NN*NN];//存边(如果选了该点,哪些点不能选)
bool vis[26];//该颜色是否被访问过/使用过(一数组两用)
void add(int x,int y) {nxt[++cnt]=h[x];to[cnt]=y;h[x]=cnt;}//加边
struct node {
int x,y,z;
node() {}
node(int x,int y,int z):x(x),y(y),z(z) {}
};//三维点
vector<node> g[26][26];//边界上的点
int _abs(int x) {return x<0?-x:x;}//手写绝对值
bool cmp(const int &x,const int &y) {return v[x].size()>v[y].size();}//根据限制多少排序
int N(const node &p) {return p.z*n*m+p.y*n+p.x;}//三维点化一维点
node P(const int &t) {return node(t%n,t/n%m,t/n/m);}//一维点化一维点
int dist(const node &a,const node &b) {return _abs(a.x-b.x)+_abs(a.y-b.y)+_abs(a.z-b.z);}//曼哈顿距离
bool range(const int &x,const int &y,const int &z) {return (x<0||x>=n||y<0||y>=m||z<0||z>=k);}//是否出界
void build() {//存储图上的边界点
for(int x=0;x<n;x++)
for(int y=0;y<m;y++)
for(int z=0;z<k;z++) {
int now=get_c();
siz[now]++,c[N(node(x,y,z))]=now;//一般读入
if(!vis[now]) col++,vis[now]=1;//颜色被使用了
}
for(int x=0;x<n;x++)
for(int y=0;y<m;y++)
for(int z=0;z<k;z++)
for(int t=0;t<6;t++) {
int xx=x+dx[t],yy=y+dy[t],zz=z+dz[t];
if(range(xx,yy,zz)) continue;
node a=node(x,y,z),b=node(xx,yy,zz);
if(c[N(a)]==c[N(b)]) continue;
g[c[N(a)]][c[N(b)]].push_back(a);//交界点
}
}
void init() {//预处理
for(int i=0;i<tot;i++)
for(int j=i+1;j<tot;j++) {
if(c[i]==c[j]) {v[i].push_back(j),v[j].push_back(i);continue;}//联通块内显然不能放
if(!g[c[i]][c[j]].size()) continue;//莫得交界
node a=P(i),b=P(j);
for(int t=0;t<g[c[i]][c[j]].size();t++) {
bool flag=0;
node aa=g[c[i]][c[j]][t];
for(int w=0;w<6;w++) {
int xx=aa.x+dx[w],yy=aa.y+dy[w],zz=aa.z+dz[w];
if(range(xx,yy,zz)) continue;
node bb=node(xx,yy,zz);
if(c[N(bb)]!=c[j]) continue;//拓展后的点不在一个联通块,说明没出界,没问题
int dis1=dist(a,aa),dis2=dist(b,bb);
if(dis1==dis2) continue;//曼哈顿距离相等,没问题
if(_abs(dis1-dis2)>1) {flag=1;break;}//曼哈顿距离太大
if(c[i]<c[j]&&dis1<dis2) {flag=1;break;}//优先级问题
if(c[i]>c[j]&&dis1>dis2) {flag=1;break;}//同上
}
if(flag) {v[i].push_back(j),v[j].push_back(i);break;}//添加上述三种可能的限制
}
}
}
bool dfs(int x,int sum) {
if(sum==col) return 1;//颜色选完了
if(tmp[rk[x]]) return dfs(x+1,sum);//这个点被访问过了
vis[c[rk[x]]]=1;//颜色被访问过了
s[top++]=rk[x];res[c[rk[x]]]--;//入栈、该颜色剩余的点减少
bool ok=1;
for(int i=h[rk[x]];i;i=nxt[i]) {
int y=to[i];
if(!tmp[y]) {
res[c[y]]--;//继续减少可用点
if(!vis[c[y]]&&!res[c[y]]) ok=0;//不能放置战舰了,剪枝2
}
tmp[y]++;//这个点被访问过了
}
if(ok&&dfs(x+1,sum+1)) return 1;//利用&&的短路性质,在能放置战舰的前提下继续向下一层搜索
for(int i=h[rk[x]];i;i=nxt[i]) {//回溯
int y=to[i];
tmp[y]--;
if(!tmp[y]) res[c[y]]++;
}
bool flag=0;
top--;//回溯出栈
vis[c[rk[x]]]=0;
if(res[c[rk[x]]]) flag=dfs(x+1,sum);//如果还能放,尝试该层别的放法。
res[c[rk[x]]]++;//回溯
return flag;
}
int main() {
int T=read();
while(T--) {
n=read(),m=read(),k=read();
tot=n*m*k;
build(),init();
for(int i=0;i<tot;i++) rk[i]=i;
sort(rk,rk+tot,cmp);
for(int i=0;i<tot;i++) pos[rk[i]]=i;//记录名次和名次的逆
for(int i=0;i<tot;i++)
for(int j=0;j<v[i].size();j++)
if(pos[v[i][j]]>pos[i]) add(i,v[i][j]);//限制多的向限制少的连边
for(int i=0;i<26;i++) res[i]=siz[i],vis[i]=0;//能选的数量等于该颜色点的数量,重置vis
dfs(0,0);
for(int i=0;i<top;i++) {//不把栈当栈用QWQ
node p=P(s[i]);
printf("%c %d %d %d
",c[s[i]]+'a',p.x,p.y,p.z);//输出答案
}
for(int i=0;i<tot;i++) tmp[i]=0,v[i].clear(),h[i]=0;//各种清空
for(int i=0;i<26;i++) for(int j=0;j<26;j++) g[i][j].clear();
for(int i=0;i<26;i++) vis[i]=siz[i]=0;
cnt=col=top=0;
}
return 0;
}