在算法程序设计竞赛中,会经常碰到对某个数N进行求大数次幂并对1e9+7取模的运算的题目,一方面求大数次幂是一个时间复杂度很高的运算(容易超时),另一方面对1e9+7取模,暗示着结果是连long long都存不下(同余定理),所以这时候快速幂取模算法就派上用场了,我们先来求a^bmodc;
算法1:直接设计,朴素
int ans = 1;
for(int i = 1;i<=b;i++)
{
ans = ans * a;
}
ans = ans % c;缺点:数字过大会溢出,而且比较费时间,
接下来介绍一下同余定理
(a +/- b) % c = (a % c +/- b % c) % c
(a * b) % c = (a % c) * (b % c) % c
a^b % c = (a % c)^b % c算法2:快速幂,根据公式
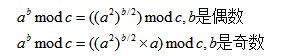
int PowerMod(int a, int b, int c)
{
int ans = 1;
a = a % c; //对刚进来的a进行取模运算,避免后面第一次求平方运算溢出
while(b)
{
if(b&1) //相当于b % 2 = = 1对二进制下的 b 进行按位与1运算,求二进制下 b 的最低位是否为1
ans = ans * a % c; //对结果进行保存
b>>=1; //相当于b = b/2;二进制下的 b 右移一位,相当于十进制下的 b 除以2
a = a * a % c;
}
return ans%c;
}