743. 网络延迟时间
有 N 个网络节点,标记为 1 到 N。
给定一个列表 times,表示信号经过有向边的传递时间。 times[i] = (u, v, w),其中 u 是源节点,v 是目标节点, w 是一个信号从源节点传递到目标节点的时间。
现在,我们从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1。
输入:times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
输出:2
深度优先搜索
以K为起点,深度优先遍历,传入距离值,若距离大于结点已知最小距离则停止深搜,否则更新当前结点
时间复杂度:O(N^N)
空间复杂度:O(N+E)
var networkDelayTime = function (times, N, K) {
/* 存各条边的信息 */
const edges = new Map();
for (let [x, y, val] of times) {
if (!edges.has(x))
edges.set(x, [[y, val]]);
else
edges.get(x).push([y, val]);
}
/* 初始化标记 */
const vis = new Array(N + 1).fill(false);
/* 初始化距离 */
const MAX = Number.MAX_SAFE_INTEGER;
const dst = new Map();
for (let i = 1; i <= N; i++) dst.set(i, MAX);
/* 深搜 */
function dfs(index, dis) {
/* 剪枝 */
if (dst.get(index) < dis) return;
/* 更新 */
dst.set(index, dis);
/* 往下遍历 */
if (edges.get(index)) {
for (let [tgt, val] of edges.get(index)) {
if (!vis[tgt]) {
vis[tgt] = true;
dfs(tgt, dis + val);
vis[tgt] = false;
}
}
}
}
dfs(K, 0);
/* 取最大值 */
let ans = 0;
for (let v of dst) {
if (v[1] === MAX) return -1;
ans = Math.max(ans, v[1]);
}
return ans;
};
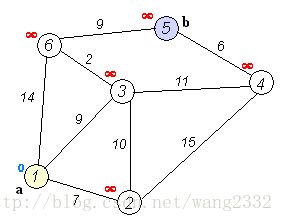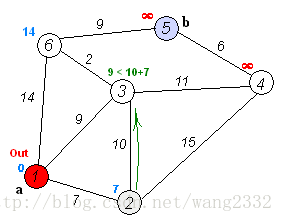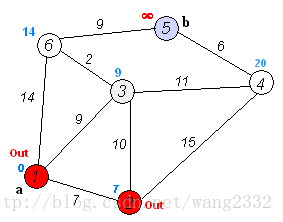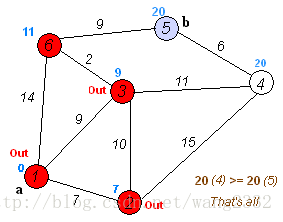
Dijkstra解法
每次找出距离K最近的点minIndex并标记,遍历minIndex相连的所有点tgt,对比K直接到tgt的距离和K经过minIndex到达tgt的距离,更新K到tgt的距离为两者中的最小值,重复该操作直到所有点均已被标记
时间复杂度:由于需要N轮更新,每轮遍历N次,所以为O(N^2)
空间复杂度:O(N+E)
var networkDelayTime = function (times, N, K) {
const edges = new Map();
const dst = new Map();
/* 转换为起点为索引的边进行存储 */
for (let [x, y, val] of times) {
if (!edges.has(x)) {
edges.set(x, [[y, val]]);
} else {
edges.get(x).push([y, val]);
}
}
/* 初始化各点到K的距离 */
const MAX = Number.MAX_SAFE_INTEGER;
for (let i = 1; i <= N; i++) dst.set(i, MAX);
dst.set(K, 0);
/* 更新每个结点 */
const vis = new Array(N + 1).fill(false);
let minIndex, min;
for (let k = 1; k <= N; k++) {
/* 找最小边 */
minIndex = -1; min = MAX;
for (let i = 1; i <= N; i++) {
if (!vis[i] && dst.get(i) < min) {
minIndex = i;
min = dst.get(i);
}
}
if (minIndex === -1) break;
/* 标记访问并更新其他相连结点 */
vis[minIndex] = true;
if (edges.has(minIndex)) {
for (let [tgt, val] of edges.get(minIndex)) {
// 对比K直接到tgt的距离和经过minIndex到达tgt的距离
dst.set(tgt, Math.min(dst.get(tgt), dst.get(minIndex) + val));
}
}
}
/* 找最大距离 */
let ans = 0;
for (let v of dst) {
//遍历Map的结果是一个数组
if (v[1] === MAX) return -1;//有不可到达的点
ans = Math.max(v[1], ans);
}
return ans;
};
SFPA算法
将被更新的结点放入队列,每次取出队头,遍历与其相关的所有结点,若相关结点值被更新,则放入到队列尾部,以便下次取出来更新后续结点
时间复杂度:最坏O(V*E),V表示入队次数
空间复杂度:O(V+E)
var networkDelayTime = function (times, N, K) {
/* 存每个节点的所有边 */
const edges = new Map();
for (let [x, y, val] of times) {
if (!edges.has(x)) {
edges.set(x, [[y, val]]);
} else {
edges.get(x).push([y, val]);
}
}
/* 初始化距离 */
const MAX = Number.MAX_SAFE_INTEGER;
const dst = new Array(N + 1).fill(MAX);
dst[K] = 0;
/* 队列中的元素会引起后续结点更新 */
const queue = [K];
while (queue.length) {
let x = queue.shift();
// 更新结点
if (edges.has(x)) {
for (let [y, val] of edges.get(x)) {
if (dst[y] > dst[x] + val) {
dst[y] = dst[x] + val;
queue.push(y);//存入队列更新y以后的结点
}
}
}
}
/* 找最大值 */
let ans = 0;
for (let i = 1; i <= N; i++) {
ans = Math.max(ans, dst[i]);
}
return ans === MAX ? -1 : ans;
};