这是填坑篇,之前写的图片旋转程序把图片变成了桌布,几个世纪后,在一个月黑风高的夜晚,我灵光乍现,何不试试双线性插值?
先上代码和效果图。
1 # !/usr/bin/env python3 2 # -*-coding:utf-8-*- 3 """ 4 双线性插值参考资料: 双线性插值原理及Python实现 - Jinglever https://www.jianshu.com/p/29e5c84ea539 5 6 如果出现错误:...If you are on Ubuntu or Debian, install libgtk2.0-dev and pkg-config 7 执行 pip3 install opencv-contrib-python 8 """ 9 import numpy as np 10 # np.set_printoptions(suppress=True) # 关闭科学计数法 11 import cv2 12 import os 13 14 15 # 旋转矩阵R 16 ANGLE = 30 # (dim=°) 17 assert 0 < ANGLE < 90 # 目前限制这个旋转范围,原因是y1, y2, y3, y4上下关系根据角度变化 18 alpha = ANGLE/360*2*np.pi 19 R_rev = np.matrix([[np.cos(alpha), np.sin(alpha)], # 逆向映射推导的旋转矩阵 20 [-np.sin(alpha), np.cos(alpha)]]) 21 print(R_rev) 22 23 # 重设图片大小 24 WIDTH, HEIGHT = 640, 480 25 26 img = cv2.imread("timg.jpg") 27 img = cv2.resize(img, (WIDTH, HEIGHT)) 28 # img_gray = np.float32(cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)) 29 img = np.float32(img) 30 print(img.shape) 31 32 # 假设已经得到旋转后的图片,利用图片边框画出图片的矩形,在矩形内遍历坐标就是图片各个像素点的坐标 33 # 注意旋转角度超过90度后边框线的上下关系会发生变化,待改进…… 34 x = np.arange(np.abs(WIDTH*np.cos(alpha)) + np.abs(HEIGHT*np.sin(alpha)), dtype=np.int32) 35 y1 = lambda x: (- x*np.tan(alpha)).astype(np.int32) 36 y2 = lambda x: (y1(x) + HEIGHT/np.cos(alpha)).astype(np.int32) 37 y3 = lambda x: (x/np.tan(alpha)).astype(np.int32) 38 y4 = lambda x: (y3(x) - WIDTH/np.sin(alpha)).astype(np.int32) 39 # 用矩形下面2条线(的最大值)确定y坐标最小值,上面2条线(的最小值)确定y坐标最大值 40 y_min = np.max(np.concatenate((y1(x).reshape(1, -1), y4(x).reshape(1, -1))), axis=0) 41 y_max = np.min(np.concatenate((y2(x).reshape(1, -1), y3(x).reshape(1, -1))), axis=0) 42 # 计算旋转后图片各像素点坐标 43 pre_index = [np.array((yi, xi)).reshape(-1, 1) for xi in x for yi in range(y_min[xi], y_max[xi]+1)] 44 45 ori_index = np.array(list(map(R_rev.dot, pre_index))).reshape(-1, 2) # 坐标变换到原图 46 hs_p, ws_p = np.hsplit(ori_index, 2) # 分离y, x坐标 47 48 ws_p = np.clip(ws_p, 0, WIDTH-1) # 限制坐标最值防止越界 49 hs_p = np.clip(hs_p, 0, HEIGHT-1) 50 51 ws_0 = np.clip(np.floor(ws_p), 0, WIDTH - 2).astype(np.int) # 找出每个投影点在原图的近邻点坐标 52 hs_0 = np.clip(np.floor(hs_p), 0, HEIGHT - 2).astype(np.int) 53 ws_1 = ws_0 + 1 54 hs_1 = hs_0 + 1 55 56 f_00 = img[hs_0, ws_0, :].T # 四个临近点的像素值 57 f_01 = img[hs_0, ws_1, :].T 58 f_10 = img[hs_1, ws_0, :].T 59 f_11 = img[hs_1, ws_1, :].T 60 61 w_00 = ((hs_1 - hs_p) * (ws_1 - ws_p)).T # 计算权重 62 w_01 = ((hs_1 - hs_p) * (ws_p - ws_0)).T 63 w_10 = ((hs_p - hs_0) * (ws_1 - ws_p)).T 64 w_11 = ((hs_p - hs_0) * (ws_p - ws_0)).T 65 66 pixels = (f_00 * w_00).T + (f_01 * w_01).T + (f_10 * w_10).T + (f_11 * w_11).T # 计算目标像素值 67 68 y_new, x_new = np.hsplit(np.array(pre_index).reshape(-1, 2), 2) # # 分离y, x坐标 69 y_new = y_new - np.min(y_new) # y坐标平移,防止图片旋转后被窗口切分 70 71 h, w = np.max(y_new), np.max(x_new) # 旋转后画布大小 72 # 像素映射 原始→新图 73 new_img = np.zeros((h+1, w+1, img.shape[2])) # (H, W, C) 74 new_img[y_new, x_new, :] = pixels # 填充像素 75 76 cv2.imwrite('./AffinedImg.jpg', new_img, [int(cv2.IMWRITE_JPEG_QUALITY),95]) 77 # 显示图片 78 cv2.imshow('img', np.array(new_img, dtype=np.uint8)) 79 cv2.waitKey(0) 80 cv2.destroyAllWindows()
原图见入坑篇。
下面是运行结果,这次我换成了彩色的:

双线性插值常用于图像的比例缩放,基本原理很容易搜索到,这里就不多说了,重点讲一下怎么把它应用到图像旋转上来。
假设输入图片是 input image,输出图片是 output image,首先回顾一下双线性插值的思路:坐标的变换是反着来的,从 output image 到 input image。即 output image 对应的整数坐标,缩放变换到 input image 后,变成浮点数坐标,然后取它4个角上的点,计算浮点数坐标的颜色,填充到 output image 对应的坐标那里。
再说回图像旋转,之前出现黑点就是因为图像的变换是从 input image 到 output image,即每个 input image 的像素坐标用旋转矩阵算到 output image 上,然后把浮点数直接量化成整数,这样就引入了量化误差,个别输出的坐标就错位了,导致有黑点(本来在黑点位置的像素因为坐标错位到别的地方去了,黑点那里就没有颜色数据了)。
应用双线性插值的解决思路:先得到 output image 对应的整数坐标,变换到 input image 后,变成浮点数坐标,然后取它4个角上的点,计算浮点数坐标的颜色,填充到 output image 对应的坐标那里。(跟上面那句一样)
那么,实现过程就分为以下几步:
1. 获取 output image 对应各个像素点坐标。
1) 假设已经得到 output image,这张图片是旋转一定角度的,俗话说就是斜着的,但是坐标系是正着的,怎么得到像素坐标?
2. 坐标映射:使用反着转的旋转矩阵(R_rev)把 output image 的坐标转到 input image 上,这个结果算出来是浮点数。
3. 双线性插值:取浮点数坐标4个角上的点,计算浮点数坐标的颜色,然后填充回 output image。大功告成!
首先回答问题 1) :
我使用了一个很简单的方法,就是靠图像边框作为边界,框出图像的矩形区域,遍历里面的所有点。
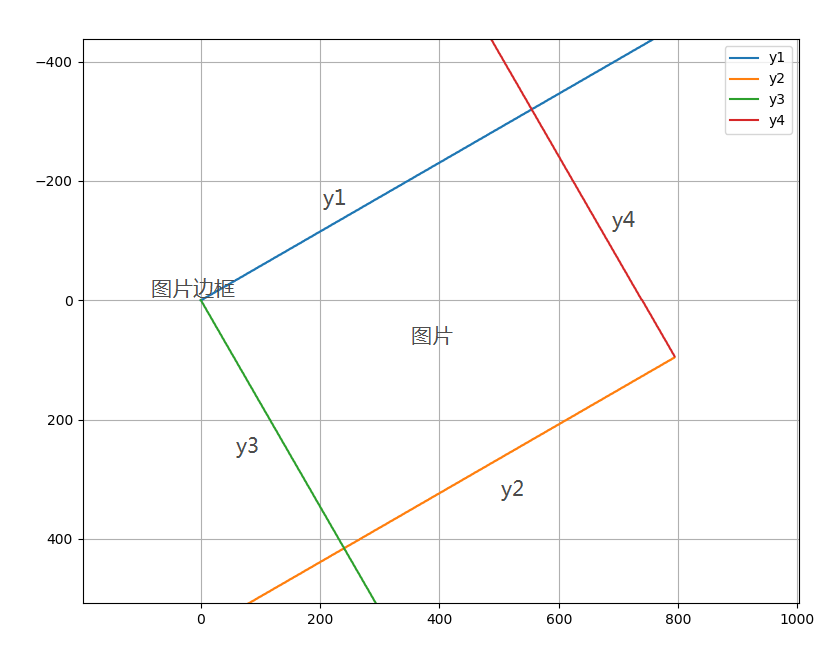
$y_{1}=-xcdot an left ( alpha ight )$
$y_{2}=-xcdot an left ( alpha ight ) + frac {HEIGHT}{cos left ( alpha ight )}$
$y_{3}=frac{x}{ an left ( alpha ight )}$
$y_{4}=frac{x}{ an left ( alpha ight )}-frac{WIDTH}{sin left ( alpha ight )}$
上图绘制了y1, y2, y3, y4四条直线,注意图片显示的坐标,y轴正方向朝下。如图所示,y1, y2, y3, y4是图片的边框线,标号是我自己随便标的,如果旋转角度在90度内,边框线的上下关系不变(y2, y3在上,y1, y4在下,注意y轴正方向朝下)。这也就是现在这个程序只能实现90度以内旋转的原因,如果要继续旋转,例如旋转120度时,就变成 y1, y3 在上,y2, y4 在下,需要修改程序。
然后是遍历图片坐标:
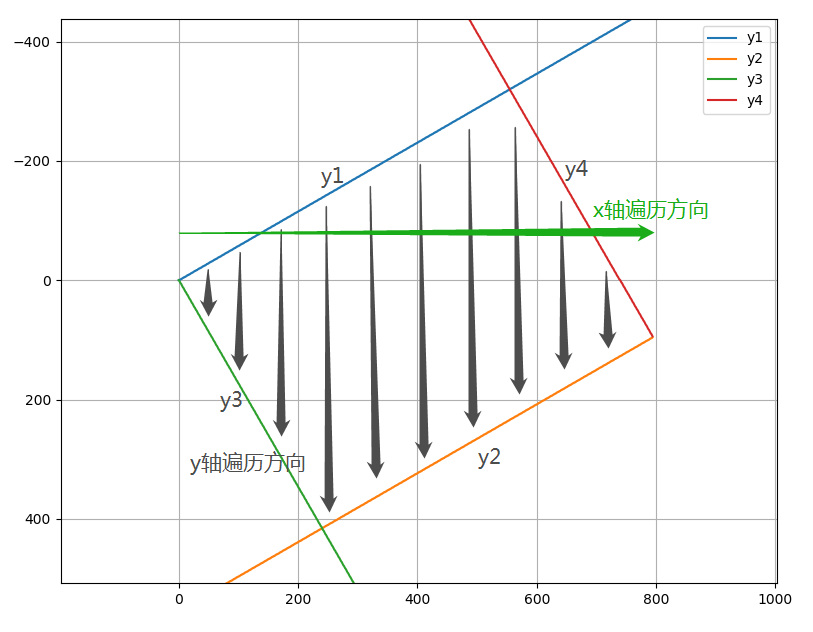
如图所示,从点 (0, 0) 开始,按照箭头方向逐列遍历图片坐标,保存到 pre_index 中。 对应代码:(理解注释里的上下关系的时候,仍然要记得y轴正方向朝下!)
# 假设已经得到旋转后的图片,利用图片边框画出图片的矩形,在矩形内遍历坐标就是图片各个像素点的坐标 # 注意旋转角度超过90度后边框线的上下关系会发生变化,待改进…… x = np.arange(np.abs(WIDTH*np.cos(alpha)) + np.abs(HEIGHT*np.sin(alpha)), dtype=np.int32) y1 = lambda x: (- x*np.tan(alpha)).astype(np.int32) y2 = lambda x: (y1(x) + HEIGHT/np.cos(alpha)).astype(np.int32) y3 = lambda x: (x/np.tan(alpha)).astype(np.int32) y4 = lambda x: (y3(x) - WIDTH/np.sin(alpha)).astype(np.int32) # 用矩形下面2条线(的最大值)确定y坐标最小值,上面2条线(的最小值)确定y坐标最大值 y_min = np.max(np.concatenate((y1(x).reshape(1, -1), y4(x).reshape(1, -1))), axis=0) y_max = np.min(np.concatenate((y2(x).reshape(1, -1), y3(x).reshape(1, -1))), axis=0) # 计算旋转后图片各像素点坐标 pre_index = [np.array((yi, xi)).reshape(-1, 1) for xi in x for yi in range(y_min[xi], y_max[xi]+1)]
到这里第1步就完成了。
然后是第2步,坐标映射。
# R = np.matrix([[np.cos(alpha), -np.sin(alpha)], # [np.sin(alpha), np.cos(alpha)]]) R_rev = np.matrix([[np.cos(alpha), np.sin(alpha)], # 逆向映射推导的旋转矩阵 [-np.sin(alpha), np.cos(alpha)]])
按照推导正向旋转矩阵的方法反推逆向旋转矩阵,就可以得到上面的结果。如果仍然难以理解,就当做反转(alpha = -alpha)
ori_index = np.array(list(map(R_rev.dot, pre_index))).reshape(-1, 2) # 坐标变换到原图
ori_index 里的坐标全部是根据 pre_index 计算来的,并不是从原图上面取点。这里计算出来的 ori_index 数据类型是浮点数。
然后是第3步,双线性插值和像素填充。
从 ori_index 开始直到计算出来 pixels 就是双线性插值的过程了,实现原理可以参考一下参考资料。
之后是像素填充:
y_new, x_new = np.hsplit(np.array(pre_index).reshape(-1, 2), 2) # # 分离y, x坐标 y_new = y_new - np.min(y_new) # y坐标平移,防止图片旋转后被窗口切分 h, w = np.max(y_new), np.max(x_new) # 旋转后画布大小 # 像素映射 原始→新图 new_img = np.zeros((h+1, w+1, img.shape[2])) # (H, W, C) new_img[y_new, x_new, :] = pixels # 填充像素
需要注意的是,旋转后的图片有一部分的坐标值是负值,实际显示的时候如果输入负坐标,图片会被分开显示,所以把旋转后的图片朝y轴正方向平移,移到所有点坐标值都大于0的地方。
现在 pixels 里已经计算出来旋转后图片所有点的像素值,像素点数据的排列方向和 pre_index 是相同的,所以直接把对应的点赋值就可以了。
最后的图片就是 new_img,插值效果还是很不错的。;-)
参考资料: