旋转卡壳-求凸包最大直径

时间复杂度：O（n）

参考：https://www.cnblogs.com/xdruid/archive/2012/07/01/2572303.html

暴力：n^2枚举凸包上的点，如果数据水的话可过。

高级做法：

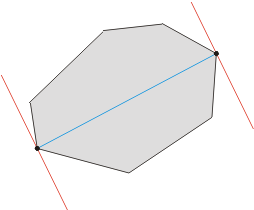
用一对平行线“卡”住凸包进行旋转。

被一对卡壳正好卡住的对应点对称为对踵点。

对锺点的具体定义不好说，不过从图上还是比较好理解的（黑色点对）。

可以证明（此处略过）对踵点的个数不超过3N/2个 也就是说对踵点的个数是O(N)的

对踵点的个数也是我们下面解决问题时间复杂度的保证。

卡壳呢，具体来说有两种情况：

1.

平行线正好卡着两个点

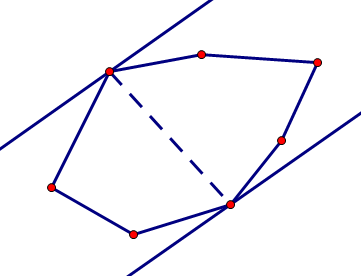
2.

平行线分别卡着一条边和两个点

而第二种情况在实现中比较容易处理，这里就只研究第二种情况。

在第二种情况中 我们可以看到 一个对踵点和对应边之间的距离比其他点要大

也就是一个对踵点和对应边所形成的三角形是最大的

具体实现：

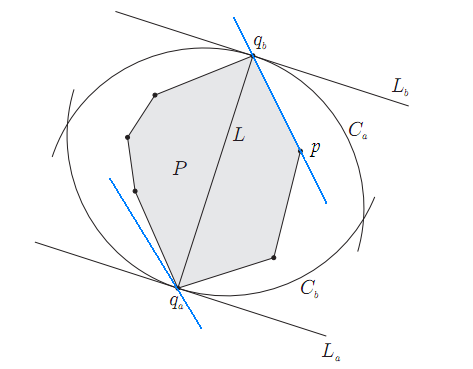
1.如果q_a，q_b是凸包上最远两点，必然可以分别过q_a，q_b画出一对平行线。通过旋转这对平行线，我们可以让它和凸包上的一条边重合,,如图中蓝色直线。可以注意到，q_a是凸包上离p和q_b所在直线最远的点

2.于是我们的思路就是枚举凸包上的所有边，对每一条边找出凸包上离该边最远的顶点，计算这个顶点到该边两个端点的距离，并记录最大的值。直观上这是一个O(n²)的算法，和直接枚举任意两个顶点一样了

3.但是注意到当我们逆时针枚举边的时候，最远点的变化也是逆时针的，这样就可以不用从头计算最远点，而可以紧接着上一次的最远点继续计算于是我们得到了O(n)的算法。

参考代码：

void rotate()
{ 
    if(top==2)//注意特殊情况 
    {
        printf("%d",(int)(dis(s[1],s[2])*dis(s[1],s[2])+eps));
        return;
    }
    s[top+1]=s[1];
    int p=3;DB ans=0;
    //cross()为叉积函数 
    for(int i=1;i<=top;++i)
    {
        while(cross(s[i],s[i+1],s[p])<cross(s[i],s[i+1],s[p+1])) 
        {
            p++;p%=top;
            if(p==0) p=top;
        }//找到距离当前直线最远的点 
        DB tmp=max(dis(s[i],s[p]),dis(s[i+1],s[p]));
        ans=max(ans,tmp);//更新答案 
    }
    //ans为最终答案 
}

 涉世浅，点染亦浅；历事深，机械亦深。