链接:https://atcoder.jp/contests/arc101/tasks/arc101_b
题意:
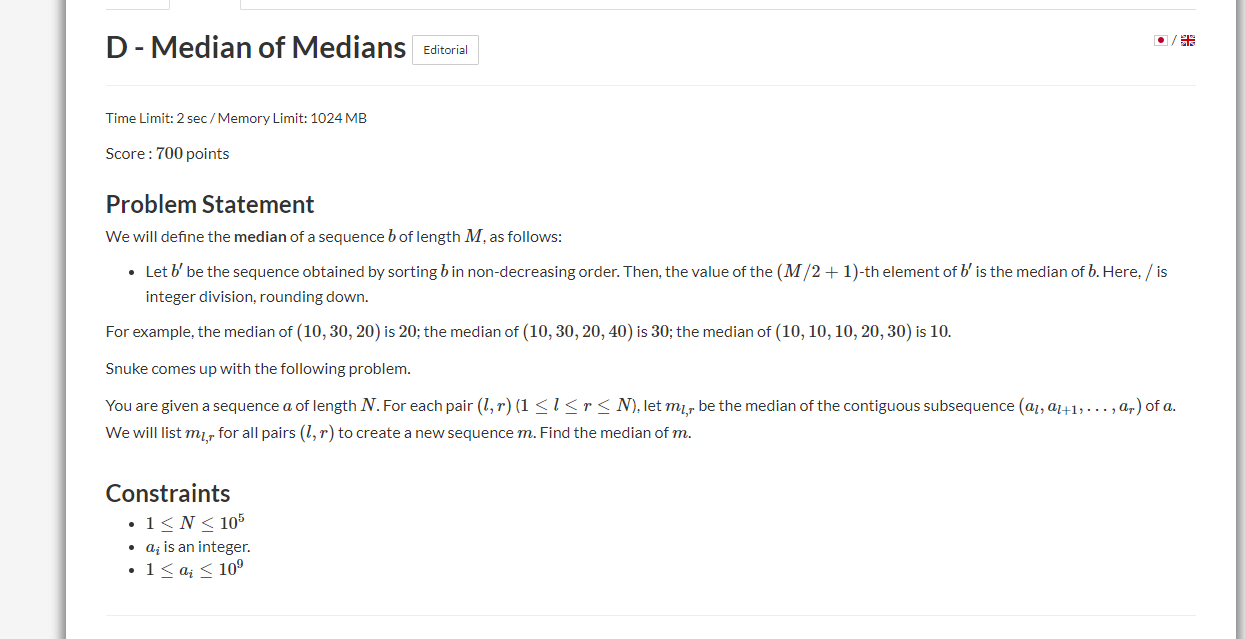
先给出中位数定义 若为奇数 就是中位数
若为偶数,则为两个中间的数中较大那个
给一个长度为N的数组,把他们任意取l,r的连续区间 ,求sort后的中位数,放在一起,组成一个新序列,然后再求中位数就是答案
求这个中位数;
考虑二分答案,
考虑求x是不是答案,
则求所有区间中大于等于x的中位数,
如何统计这个数
首先 总个数肯定是cnt=n*(n+1)/2;
把一个区间大于x的设为1,小于x的设为-1 ,那么这个区间的中位数>=x的条件就是加合>=0;
考虑维护一个前缀和,如果sumr-suml>=0 那么这个区间的中位数 就>=x
然后用一个树状数组去维护 l, 每次用r去统计答案即可
#include <algorithm> #include <iostream> #include <cstdlib> #include <cstring> #include <cstdio> #include <cmath> #define re register using namespace std; typedef long long ll; inline int read() { int X=0,w=1; char c=getchar(); while (c<'0'||c>'9') { if (c=='-') w=-1; c=getchar(); } while (c>='0'&&c<='9') X=X*10+c-'0',c=getchar(); return X*w; } const int N=100000+10; int n,mx; int a[N],s[N],ss[N]; int c[N<<1]; inline int lowbit(int x) { return x&-x; } inline void add(int x,int y) { for (;x<=mx;x+=lowbit(x)) c[x]+=y; } inline int query(int x) { int res=0; for (;x;x-=lowbit(x)) res+=c[x]; return res; } inline int check(int mid) { memset(c,0,sizeof(c)),mx=0; for (re int i=1;i<=n;++i) { if (s[i]<mid) ss[i]=-1; else ss[i]=1; } ll res=0; for (re int i=1;i<=n;++i) ss[i]+=ss[i-1],res+=(ss[i]>=0); for (re int i=1;i<=n;++i) ss[i]+=n+1,mx=max(mx,ss[i]); for (re int i=1;i<=n;++i) res+=query(ss[i]),add(ss[i],1); ll cnt=1ll*n*(n-1)/2+n; return cnt-res<cnt/2+1; //这个地方,其实中位数还是有可能不是x,但是不断二分到最大的满足条件的,一定是 } int main() { cin>>n; for(int i=1;i<=n;i++) { cin>>s[i]; a[i]=s[i]; } sort(a+1,a+1+n); int l=1,r=n; int ans=0; while(l<=r) { int mid=(l+r)>>1; if(check(a[mid])) { l=mid+1; ans=a[mid]; } else { r=mid-1; } } cout<<ans<<endl; return 0; }