虚树
主要解决树上每次询问k个关键点,满足(sum k)是线性的问题
性质1
将k个点按dfn序排序后,
集合({)相邻两点lca(}={)任意两点lca(})
反证:
设(S={)相邻两点lca(})
设按dfn序排序后有两点x,y((x<y)且(y-x>1))
我们假设x,y的lca为Anc,且Anc(
ot in S)
则x,y属于Anc的两棵不同子树
根据dfn序的性质对于点z((x<z<y))
z一定是Anc的一个子树
①x,z属于Anc的同一子树,则lca(z,y)=Anc
②z,y属于Anc的同一子树,则lca(x,z)=Anc
③x,z,y属于Anc的三棵不同子树,则lca(x,z)=lca(z,y)=Anc
性质2
可以用树链的并减去虚树总根到root距离得到虚树边权和
性质3
虚树中叶子节点必为关键点(关键点存法可以使用时间戳)
性质4
对于虚树上任意一点x,不会存在x的一个子树没有任何关键点
构建
先按dfn序排序,算出总lca为根
先在栈中插入根,
对于每个点如果在栈顶的子树中,直接入队
否则进行一些出队,大概如图下:
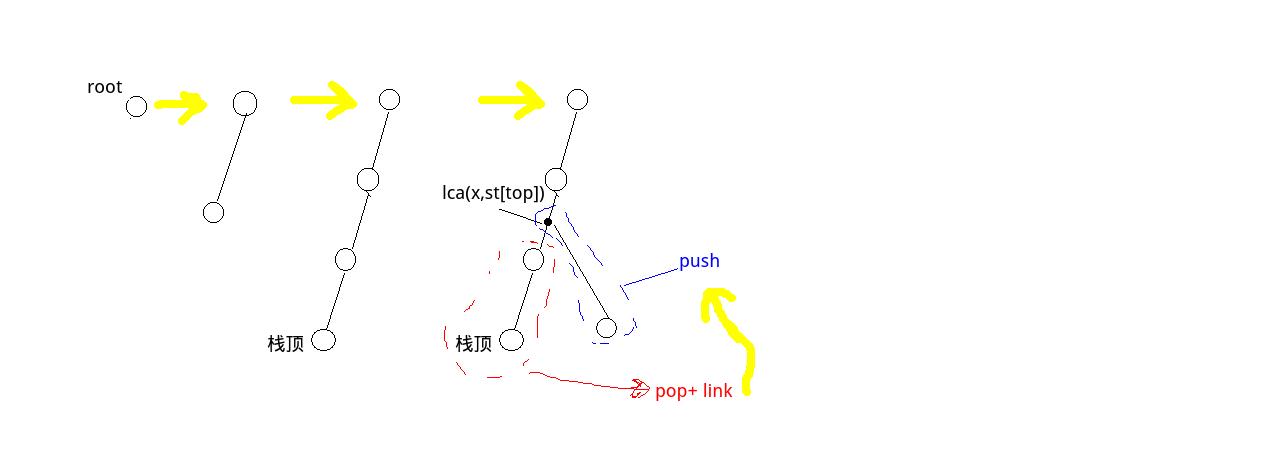
int vbuild(int z){
int rt;
int i,x,anc;
sort(que+1,que+z+1,cmp);
rt=que[1];
for(i=1;i<z;i++){
x=LCA(que[i],que[i+1]);
hd[x]=0; kd[x]=2;//各种初始化
if(dep[x]<dep[rt]) rt=x;//找到总rt
}
//先初始化lca再初始化关键点,避免出现关键点是lca被判错kd
//hd[1]=0; kd[1]=2;//如果题目要求算上1就加这一行,记得是在算下面之前写,理由同上
for(i=1;i<=z;i++){
x=que[i];
hd[x]=0; kd[x]=1;//hd[]是静链头
}
td=tot=0;//td是静链标号,tot是栈元素个数
st[++tot]=rt;
for(i=1;i<=z;i++){
x=que[i];
anc=LCA(x,st[tot]);
if(anc==st[tot]) st[++tot]=x;//情况①
else{
while( tot>1 && anc==LCA(st[tot-1],x)){
addlink(st[tot-1],st[tot]);
tot--;
}//pop && link
addlink(anc,st[tot]);//link
st[tot]=anc;
st[++tot]=x;
//push
}
}
for(i=1;i<tot;i++) addlink(st[i],st[i+1]);//pop && link
return rt;
}
注意点
1.lca不是瓶颈时树剖比较方便,top重名则把stack的计数器改为tot
2.dp时特别特别注意对1类点(关键点)和2类点(非关键点)的分类讨论