题目大意:
有边权点权的树,动态修改点权
每次修改后求带权重心x ((minimize) (S=sum_i val[i]*dist[x][i]))
分析:
从暴力找突破口:
对于边x,y,设长度为len,切断后x半边树权值和为(w_1),y半边树为(w_2)
若从重心从x转到到y,则(S+w_1*len-w_2*len)
y比x优当且仅当(w_2>w_1)
设当前根为root,若root的一儿子x,满足(w_x>w_{root}-w_x),则x更优,且可以证明(w_x>frac {w_{root}} 2),即不会存在第二个儿子y也比root优
做法:
暴力做法深度无保证,但(w_x>w_{root}-w_x)可以确定答案在x子树
我们用点分治树保证深度
新的问题:点分治树怎么求w
对于边x,y,设x半边树中所有点到x距离为(d_1),y半边树中所有点到y距离为(d_2)
所有点到x距离为(d_1+d_2+w_2*len)
所有点到y距离为(d_1+d_2+w_1*len)
可以了啊,这就是动态点分治模板了
询问复杂度(nlog^2n)
后来信息队一位善于创新的大神想到了nlogn的方法
x为rt,y为点分儿子时
x在上则两边权值和分别为w(y)和w(root)-w(y)
y在上则两边权值和分别为w(root)-w(x)+w(y)和w(x)-w(y)
乍一看非常正确,用rmq求个lca就可以O(1)判上下,超简便维护
但如果如图 :
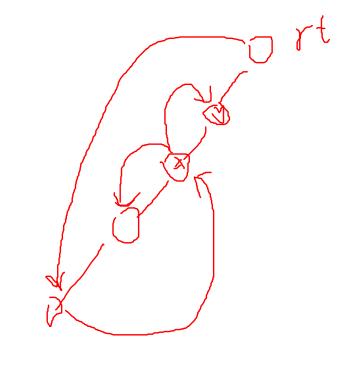
兜来兜去的图发现bug多多
吸取经验
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cctype>
using namespace std;
typedef long long LL;
const int M=100007;
const int N=M*20*2;
inline int rd(){
int x=0;bool f=1;char c=getchar();
for(;!isdigit(c);c=getchar())if(c=='-')f=0;
for(;isdigit(c);c=getchar())x=x*10+c-48;
return f?x:-x;
}
int n,m;
int g[M],te;
struct edge{
int y,next;
LL d;
}e[M<<1];
void addedge(int x,int y,LL d){
e[++te].y=y;
e[te].d=d;
e[te].next=g[x];
g[x]=te;
}
int fir[M],td;
struct down{
int y;//点分儿子
int son;//亲儿子
int next;
}dw[M];
void adddw(int x,int y,int son){
dw[++td].y=y;
dw[td].son=son;
dw[td].next=fir[x];
fir[x]=td;
}
int hd[M],tu;
struct uppp{
int all,sub,next;
LL dis;
}up[N];
void addup(int x,int all,int sub,LL dis){
up[++tu].all=all;
up[tu].sub=sub;
up[tu].dis=dis;
up[tu].next=hd[x];
hd[x]=tu;
}
struct node{
LL sum,val;
}a[M<<1];
int idrt,idsub,nw;
int sz[M],vis[M];
int mi,size,rt,root;
void getsz(int x,int fa){
sz[x]=1;
int p,y;
for(p=g[x];p;p=e[p].next)
if(!vis[y=e[p].y]&&y!=fa){
getsz(y,x);
sz[x]+=sz[y];
}
}
void getrt(int x,int fa){
int f,p,y;
f=size-sz[x];
for(p=g[x];p;p=e[p].next)
if(!vis[y=e[p].y]&&y!=fa){
getrt(y,x);
f=max(f,sz[y]);
}
if(f<mi) mi=f,rt=x;
}
void dfs(int x,int fa,LL dis){
addup(x,idrt,idsub,dis);
int p,y;
for(p=g[x];p;p=e[p].next)
if(!vis[y=e[p].y]&&y!=fa){
dfs(y,x,dis+e[p].d);
}
}
void work(int frm,int drt){
getsz(frm,0);
mi=size=sz[frm];
getrt(frm,0);
int x=rt,p,y;
vis[x]=1;
idrt=++nw;
addup(x,idrt,-1,0);
if(drt) adddw(drt,x,frm);
else root=x;
for(p=g[x];p;p=e[p].next)
if(!vis[y=e[p].y]){
idsub=++nw;
dfs(y,x,e[p].d);
}
for(p=g[x];p;p=e[p].next)
if(!vis[y=e[p].y]) work(y,x);
}
void update(int x,LL y){
int p;
for(p=hd[x];p;p=up[p].next){
a[up[p].all].val+=y;
a[up[p].all].sum+=y*up[p].dis;
if(up[p].sub!=-1){
a[up[p].sub].val+=y;
a[up[p].sub].sum+=y*up[p].dis;
}
}
}
LL get(int x){
LL res=0;
int p;
for(p=hd[x];p;p=up[p].next){
res+=a[up[p].all].sum;
res+=a[up[p].all].val*up[p].dis;
if(up[p].sub!=-1){
res-=a[up[p].sub].sum;
res-=a[up[p].sub].val*up[p].dis;
}
}
return res;
}
int anst;
void find(int x){
int p,y,bb=1;
for(p=fir[x];p;p=dw[p].next)
if(get(x)>=get(dw[p].son)){
bb=0;
find(dw[p].y);
break;
}
if(bb) anst=x;
}
int main(){
int i,x,y,z;
n=rd();m=rd();
for(i=1;i<n;i++){
x=rd(),y=rd(),z=rd();
addedge(x,y,z);
addedge(y,x,z);
}
work(1,0);
for(i=1;i<=m;i++){
x=rd(),y=rd();
update(x,y);
find(root);
printf("%lld
",get(anst));
}
return 0;
}