三类基于贪心思想的区间覆盖问题

一、区间完全覆盖问题

问题描述：给定一个长度为m的区间，再给出n条线段的起点和终点（注意这里是闭区间），求最少使用多少条线段可以将整个区间完全覆盖。

样例：一个长度为8的区间，可选的线段有[2,6]，[1,4]，[3,6]，[3,7]，[6,8]，[2,4]，[3,5]。

求解过程：

1、将每一条线段按左端点递增顺序排列，如果左端点相同，按右端点递增顺序排列，排完序后为[1,4]，[2,4]，[2,6]，[3,5]，[3,6]，[3,7]，[6,8]；

2、设置一个变量表示已覆盖到的区间右端点，在剩下的线段中找出所有左端点小于等于当前已覆盖到的区间右端点的线段，选择右端点最大并且大于当前已覆盖到的区间右端点，重复以上操作直至覆盖整个区间；

3、模拟过程：假设第一次加入[1,4]，那么下一次能够选择的线段有[2,6]，[3,5]，[3,6]，[3,7]，由于3小于4且7最大，所以下一次选择[3,7]进行覆盖，最后一次只能选择[6,8]，这个时候刚好覆盖长为8的区间-->break；即所选3条线段就能覆盖长度为8的大区间；

4、贪心证明：

要求用最少的线段进行覆盖，那么选取的线段必然要尽量长，而已覆盖到的区域之前的地方已经不用考虑了，可以理解成所有可覆盖的左端点都已被覆盖了，那么能够使得线段更长的取决于右端点，左端点没有太大的意义，所以选择右端点来覆盖。

题解报告：NYOJ #12 喷水装置（二）

描述

有一块草坪，横向长w,纵向长为h,在它的橫向中心线上不同位置处装有n(n<=10000)个点状的喷水装置，每个喷水装置i喷水的效果是让以它为中心半径为Ri的圆都被润湿。请在给出的喷水装置中选择尽量少的喷水装置，把整个草坪全部润湿。

输入

第一行输入一个正整数N表示共有n次测试数据。每一组测试数据的第一行有三个整数n,w,h，n表示共有n个喷水装置，w表示草坪的横向长度，h表示草坪的纵向长度。随后的n行，都有两个整数xi和ri,xi表示第i个喷水装置的的横坐标（最左边为0），ri表示该喷水装置能覆盖的圆的半径。

输出

每组测试数据输出一个正整数，表示共需要多少个喷水装置，每个输出单独占一行。如果不存在一种能够把整个草坪湿润的方案，请输出0。

样例输入

2
2 8 6
1 1
4 5
2 10 6
4 5
6 5

样例输出

1
2
解题思路：典型的区间完全覆盖问题。由于喷水装置是安置在横向中心线上并且圆具有对称性，故只需取高度的一半，然后将每个喷水装置能够覆盖的区间范围映射成在x轴的长度，然后按上面的方法贪心选线段即可。
AC代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=10005;
int t,n,k,cnt,pos,beg;double w,h,lb,xi,ri,maxv;pair<double,double> itv[maxn];bool flag;
int main(){
    while(cin>>t){
        while(t--){
            cin>>n>>w>>h;h/=2.0;pos=cnt=0;//h取一半
            for(int i=0;i<n;++i){
                cin>>xi>>ri;
                if(ri<h)continue;//ri==h也要算
                itv[pos].first=xi-sqrt(ri*ri-h*h);
                itv[pos++].second=xi+sqrt(ri*ri-h*h);
            }
            sort(itv,itv+pos);lb=0;beg=0;flag=false;
            if(itv[0].first>0){cout<<0<<endl;continue;}//按左端点排序只需查看最左边的端点是否满足条件即可，最右边的端点在下面有判断
            while(lb<w){
                maxv=0;
                for(k=beg;k<pos&&itv[k].first<=lb;++k)//itv[k].first<=lb这样保证整个区间是连续的，即草坪都会被润湿
                    maxv=max(maxv,itv[k].second);//找线段左端点在lb以内右端点能覆盖到的最远距离
                if(maxv>lb)cnt++,lb=maxv,beg=k;//如果有一条线段右端点比当前已覆盖的区间右端点lb还大，那么就更新已覆盖的右端点值，同时计数器加1
                else {flag=true;break;}//否则说明不能覆盖整个区间，直接退出，输出0
            }
            if(flag)cout<<0<<endl;
            else cout<<cnt<<endl;
        }
    }
    return 0;
}

题解报告：NYOJ #6 喷水装置（一）

描述

现有一块草坪，长为20米，宽为2米，要在横中心线上放置半径为Ri的喷水装置，每个喷水装置的效果都会让以它为中心的半径为实数Ri(0<Ri<15)的圆被湿润，这有充足的喷水装置i（1<i<600)个，并且一定能把草坪全部湿润，你要做的是：选择尽量少的喷水装置，把整个草坪的全部湿润。

输入

第一行m表示有m组测试数据；

每一组测试数据的第一行有一个整数数n，n表示共有n个喷水装置，随后的一行，有n个实数ri，ri表示该喷水装置能覆盖的圆的半径。

输出

输出所用装置的个数

样例输入

2
5
2 3.2 4 4.5 6 
10
1 2 3 1 2 1.2 3 1.1 1 2

样例输出

2
5

解题思路：将每个能喷洒到草坪边缘的喷水装置的喷洒范围映射成在x轴的长度，然后按线段长度递增顺序排列，再从后往前贪心选线段即可得到选择最少的喷水装置来润湿整个草坪。

AC代码：

#include<bits/stdc++.h>
using namespace std;
int t,n,cnt;double ans,ri,dt[605];
int main(){
    while(cin>>t){
        while(t--){
            cin>>n;ans=0;cnt=0;
            for(int i=0;i<n;++i)cin>>ri,dt[i]=ri>1?sqrt(ri*ri-1):0;//这里可以设置为0，因为题目已经保证一定可以将草坪全部润湿
            sort(dt,dt+n);
            for(int i=n-1;ans<=10.0&&i>=0;--i)cnt++,ans+=dt[i];//从后往前能选出最少数量的喷水装置，且一定能将草坪润湿
            cout<<cnt<<endl;
        }
    }
    return 0;
}

 二、最大不相交区间数问题

问题描述：数轴上有n个区间$ [a_i,b_i] $，要求选择尽量多个区间，使得这些区间两两没有公共点。

样例：数轴上有7个区间，可选的区间有[2,6]，[1,4]，[3,6]，[3,7]，[6,8]，[2,4]，[3,5]。

求解过程：

1、按区间右端点递增顺序排列，如果右端点相同，按左端点递增顺序排序，排完序后为[1,4]，[2,4]，[3,5]，[2,6]，[3,6]，[3,7]，[6,8]；
2、第一次选择[1,4]，接下来只能选择[6,8]，即当前数轴上最多只能选择两个不相交的区间。

3、贪心证明：为了选择更多的区间个数，先按区间右端点递增顺序排列，然后顺序处理每个区间，如果它与当前已选的所有区间都没有相交，则选择该区间，否则不选。接下来证明区间左端点a1,a2…对右端点没有影响：

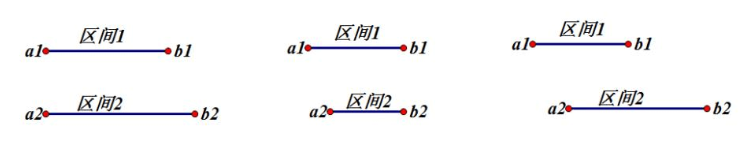
①当a1>a2时，区间2包含区间1，显然不能选择区间2，因为选择区间1会留下更多的区域。不仅区间2如此，以后所有区间中只要有一个i满足a1>ai，i都不要选，所以此种情况下，选择区间1是明智的，与策略一致。

②排除情况1后，一定有a1<=a2<=a3……，此时选择区间1是最优策略，说明无论左端点是大是小，只要对区间右端点进行排序，然后贪心选择不相交的区间就可得到数轴上最多不相交的区间个数，即这个策略是正确的。

 

题解报告：NYOJ #14 会场安排问题

描述

学校的小礼堂每天都会有许多活动，有时间这些活动的计划时间会发生冲突，需要选择出一些活动进行举办。小刘的工作就是安排学校小礼堂的活动，每个时间最多安排一个活动。现在小刘有一些活动计划的时间表，他想尽可能的安排更多的活动，请问他该如何安排。

输入

第一行是一个整型数m(m<100)表示共有m组测试数据。
每组测试数据的第一行是一个整数n(1<n<10000)表示该测试数据共有n个活动。
随后的n行，每行有两个正整数Bi,Ei(0<=Bi,Ei<10000),分别表示第i个活动的起始与结束时间（Bi<=Ei)

输出

对于每一组输入，输出最多能够安排的活动数量。
每组的输出占一行

样例输入

2
2
1 10
10 11
3
1 10
10 11
11 20

样例输出

1
2
解题思路：按结束时间早进行排序，然后贪心选择不相交区间即可。
AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=10005;
int t,n,tmp,ans;pair<int,int> itv[maxn];
int main(){
    while(cin>>t){
        while(t--){
            cin>>n;
            for(int i=0;i<n;++i)cin>>itv[i].second>>itv[i].first;
            sort(itv,itv+n);tmp=-1;ans=0;//按结束时间早进行排序
            for(int i=0;i<n;++i)
                if(tmp<itv[i].second)ans++,tmp=itv[i].first;
            cout<<ans<<endl;
        }
    }
    return 0;
}

三、区间选点问题

问题描述：数轴上有n个闭区间 $[a_i,b_i] $，要求选取尽量少的点，使得每个区间内都至少有一个点（不同区间内含的点可以是同一个）。

样例略。

求解过程：

1、按左端点递增顺序排序，如果左端点相同，按右端点递增顺序排序，个人觉得这种比较好理解，当然也可以按右端点递增顺序排序。

2、①从第一个区间右端点开始贪心往后找，如果下一个区间的左端点大于当前已选区间的右端点，说明要新开一个点，计数器加1，同时更新右区间能覆盖的最远距离；②如果下一个区间右端点小于当前已选区间的右端点，说明共享的线段范围缩短了，那么就更新区间右端点为下一个区间右端点，重复以上操作，直至筛选完所有区间。

贪心证明：为了选择最少的点使得每个区间内至少含有一个点，考虑按区间左端点递增顺序排序，如果左端点相同，则按区间右端点递增顺序排序，然后以第一个区间右端点作为第一个点能覆盖的最大范围。①当b1>b2时，显然此时一个点能覆盖最大的区域右边界变为b2，同理，以后只要满足 $ b_1 > b_i $，一个点能覆盖的区域右边界就会变为 $ b_i $，显然这是正确的；②当b1<a2时，显然一个点不能覆盖到区间2上，所以需新开一个点，此时能覆盖的区域最右边界变为b2，同理，以后只要满足 $ b1 < a_i $，则都要新开一个点，并且其能覆盖的区域右边界将变为 $ b_i $，显然这也是正确的；③ 当b1<b2时，显然区间1和区间2有公共的部分，但此时一个点能覆盖的区域最右边界还是为 b1，无需更新区域最右边界，同理，对于以后只要满足 $ b_1<b_i $，都无需新开一个点，也无需更新能覆盖区域的最右边界，显然这也是正确的。综上，按区间左端点递增的顺序排序，再按规则贪心选点的策略是正确的。

题解报告：NYOJ #891 找点

描述

上数学课时，老师给了LYH一些闭区间，让他取尽量少的点，使得每个闭区间内至少有一个点。但是这几天LYH太忙了，你们帮帮他吗？

输入

多组测试数据。
每组数据先输入一个N，表示有N个闭区间（N≤100)。
接下来N行，每行输入两个数a，b(0≤a≤b≤100），表示区间的两个端点。

输出

输出一个整数，表示最少需要找几个点。

样例输入

4
1 5
2 4
1 4
2 3
3
1 2
3 4
5 6
1
2 2

样例输出

1
3
1
解题思路：按左端点递增顺序排序，然后按上面的求解方法贪心选点即可。
AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=105;
int n,tmp,ans;pair<int,int> itv[maxn];
int main(){
    while(cin>>n){
        for(int i=0;i<n;++i)cin>>itv[i].first>>itv[i].second;
        sort(itv,itv+n);tmp=itv[0].second;ans=1;
        for(int i=0;i<n;++i){
            if(tmp<itv[i].first)ans++,tmp=itv[i].second;
            else if(tmp>itv[i].second)tmp=itv[i].second;
        }
        cout<<ans<<endl;
    }
    return 0;
}

题解报告：poj 1328 Radar Installation

Description

Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d. 
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates. 
 
Figure A Sample Input of Radar Installations

Input

The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases. 
The input is terminated by a line containing pair of zeros 

Output

For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.

Sample Input

3 2
1 2
-3 1
2 1

1 2
0 2

0 0

Sample Output

Case 1: 2
Case 2: 1
解题思路：典型的区间选点，将雷达能覆盖的范围映射为x轴上的线段长度，然后贪心区间选点即可。
AC代码：

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int maxn=1005;
int n,d,ans,pos,cnt=1,x,y;double tmp;
struct node{double l,r;}point[maxn];
bool cmp(node a,node b){return a.l<b.l;}
int main(){
    while(cin>>n>>d&&(n|d)){//注意这里：n|d，表示n和d同时为0时，程序才退出
        ans=1;pos=0;
        for(int i=0;i<n;++i){
            cin>>x>>y;
            if(y>d){ans=-1;continue;}//根号下只能为非负数
            point[pos].l=1.0*x-sqrt(1.0*d*d-y*y);//以每个岛屿为圆心，半径为d画圆，其与x轴最后只有两个交点
            point[pos++].r=1.0*x+sqrt(1.0*d*d-y*y);
        }
        sort(point,point+pos,cmp);tmp=point[0].r;
        for(int i=1;i<pos&&ans!=-1;++i){
            if(tmp<point[i].l){ans++;tmp=point[i].r;}//如果已选线段与当前线段不相交，那么就设置一个新的雷达，然后更新tmp为其右端点值
            else if(tmp>point[i].r)tmp=point[i].r;//可以覆盖掉下一条线段，但此时区间右端点缩短为下一条线段的右端点，说明覆盖的范围缩短了
        }
        cout<<"Case "<<cnt++<<": "<<ans<<endl;
    }
    return 0;
}