入门母函数实战例题（带限制数量）

题解报告：hdu 2082 找单词（母函数）

Problem Description

假设有x1个字母A， x2个字母B,..... x26个字母Z，同时假设字母A的价值为1，字母B的价值为2,..... 字母Z的价值为26。那么，对于给定的字母，可以找到多少价值<=50的单词呢？单词的价值就是组成一个单词的所有字母的价值之和，比如，单词ACM的价值是1+3+14=18，单词HDU的价值是8+4+21=33。(组成的单词与排列顺序无关，比如ACM与CMA认为是同一个单词）。

Input

输入首先是一个整数N，代表测试实例的个数。
然后包括N行数据，每行包括26个<=20的整数x1,x2,.....x26.

Output

对于每个测试实例，请输出能找到的总价值<=50的单词数,每个实例的输出占一行。

Sample Input

2 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

9 2 6 2 10 2 2 5 6 1 0 2 7 0 2 2 7 5 10 6 10 2 10 6 1 9

Sample Output

7

379297

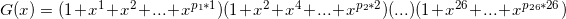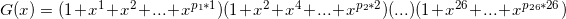解题思路：生成函数：，其中p_i*i<=50，pi*i表示第i个字母选取pi个的价值。因为题目要求的是价值总和不超过50的所有方案数，所以只需将指数按0～50枚举即可，最后累加价值不超过50的所有方案数即可。

AC代码：

#include<bits/stdc++.h>
using namespace std;
int t,n,x,sum,c1[55],c2[55];
int main(){
    while(~scanf("%d",&t)){
        while(t--){
            memset(c1,0,sizeof(c1));
            memset(c2,0,sizeof(c2));
            c1[0]=1;sum=0;
            for(int i=1;i<=26;++i){//26个多项式相乘
                scanf("%d",&x);
                for(int j=0;j<=50;++j)//指数：0~50
                    for(int k=0;k<=x&&j+k*i<=50;++k)//每两项相乘之后的指数不超过50且对应个数小于或等于x
                        c2[j+k*i]+=c1[j];
                for(int j=0;j<=50;++j)
                    c1[j]=c2[j],c2[j]=0;
            }
            for(int i=1;i<=50;++i)sum+=c1[i];//从价值1开始累加价值不超过50的所有系数即为方案总数，因为0个字母不是一个单词
            printf("%d
",sum);
        }
    }
    return 0;
}

题解报告：hdu 2079 选课时间（母函数）

Problem Description

又到了选课的时间了，xhd看着选课表发呆，为了想让下一学期好过点，他想知道学n个学分共有多少组合。你来帮帮他吧。（xhd认为一样学分的课没区别）

Input

输入数据的第一行是一个数据T，表示有T组数据。
每组数据的第一行是两个整数n(1 <= n <= 40)，k(1 <= k <= 8)。
接着有k行，每行有两个整数a(1 <= a <= 8),b(1 <= b <= 10)，表示学分为a的课有b门。

Output

对于每组输入数据，输出一个整数，表示学n个学分的组合数。

Sample Input

2

2 2

1 2

2 1

40 8

1 1

2 2

3 2

4 2

5 8

6 9

7 6

8 8

Sample Output

2

445

解题思路：数据较小，直接用母函数暴力或者dp一下即可！注意dp：学分为a的b门课程认为都是相同的，也就是有b个a，即要求选出序列数（即从每种学分中挑选出k'个学分组合成和为n的不重复序列数）相加和为n，求方案数。此时不能用二进制解，因为这道题和多重背包是有区别的，举个栗子：当n=4，k=2时，a1=1,b1=8;a2=2,b2=4;则和为n=4的有3种组合：①4个1；②2个2；③2个1和1个2。而如果用二进制的话，j-val[i]时就会出现重复计算方案数，因此需要在01背包的基础上多增加一维，表示该种物品在状态j∈[n,m*a[i]≤j]下选择m∈[1,b[i]]门课程组成学分为j的方案数。而如果用母函数做就不用考虑这些情况，直接套公式即可。

AC代码一(15ms)：

#include<bits/stdc++.h>
using namespace std;
int t,n,m,a,b,c1[50],c2[50];
int main(){
    while(~scanf("%d",&t)){
        while(t--){
            scanf("%d%d",&n,&m);
            memset(c1,0,sizeof(c1));
            memset(c2,0,sizeof(c2));c1[0]=1;
            while(m--){
                scanf("%d%d",&a,&b);
                for(int j=0;j<=n;++j)
                    for(int k=0;k<=b&&j+k*a<=n;++k)
                        c2[j+k*a]+=c1[j];
                for(int j=0;j<=n;++j)
                    c1[j]=c2[j],c2[j]=0;
            }
            printf("%d
",c1[n]);
        }
    }
    return 0;
}

AC代码二：多重背包计数转化成01背包。

#include<bits/stdc++.h>
using namespace std;
int t,n,k,a[9],b[11],dp[41];
int main(){
    while(cin>>t){
        while(t--){
            cin>>n>>k;memset(dp,0,sizeof(dp));dp[0]=1;
            for(int i=1;i<=k;++i)cin>>a[i]>>b[i];
            for(int i=1;i<=k;++i)
                for(int j=n;j>=a[i];--j)//01背包
                     for(int m=1;m<=b[i]&&m*a[i]<=j;++m)//每个状态j下可以选择一个或多个同种物品
                        dp[j]+=dp[j-m*a[i]];
            cout<<dp[n]<<endl;
        }
    }
    return 0;
}

题解报告：hdu 1085 Holding Bin-Laden Captive!（母函数）

Problem Description

We all know that Bin-Laden is a notorious terrorist, and he has disappeared for a long time. But recently, it is reported that he hides in Hang Zhou of China! 
“Oh, God! How terrible! ”
Don’t be so afraid, guys. Although he hides in a cave of Hang Zhou, he dares not to go out. Laden is so bored recent years that he fling himself into some math problems, and he said that if anyone can solve his problem, he will give himself up! 
Ha-ha! Obviously, Laden is too proud of his intelligence! But, what is his problem?
“Given some Chinese Coins (硬币) (three kinds-- 1, 2, 5), and their number is num_1, num_2 and num_5 respectively, please output the minimum value that you cannot pay with given coins.”
You, super ACMer, should solve the problem easily, and don’t forget to take $25000000 from Bush!

Input

Input contains multiple test cases. Each test case contains 3 positive integers num_1, num_2 and num_5 (0<=num_i<=1000). A test case containing 0 0 0 terminates the input and this test case is not to be processed.

Output

Output the minimum positive value that one cannot pay with given coins, one line for one case.

Sample Input

1 1 3 0 0 0

Sample Output

4

解题思路：题意就是给你num_1个一元硬币，num_2个两元硬币，num_5个五元硬币，问不能凑出来的第一个面额是多少。

G(x)=(1+x^1+x^2+...+x^num_1)(1+x^2+x^4+...+x^(2*num_2))(1+x^5+x^10+...+x^(5*num_3))。母函数O(n^2)暴力模拟即可。

AC代码一(140ms)：

#include<bits/stdc++.h>
using namespace std;
const int a[3]={1,2,5};
int sum,num[3],c1[8005],c2[8005];
int main(){
    while(~scanf("%d%d%d",&num[0],&num[1],&num[2])&&(num[0]+num[1]+num[2])){
        memset(c1,0,sizeof(c1));
        memset(c2,0,sizeof(c2));c1[0]=1;
        sum=num[0]+num[1]*2+num[2]*5;//这些硬币能凑出的最大面额为sum元
        for(int i=0;i<3;++i){
            for(int j=0;j<=sum;++j)
                for(int k=0;k<=num[i]&&j+k*a[i]<=sum;++k)
                    c2[j+k*a[i]]+=c1[j];
            for(int j=0;j<=sum;++j)
                c1[j]=c2[j],c2[j]=0;
        }
        for(int i=1;i<=sum+1;++i)//可能都凑出1~sum元，此时一定凑不出sum+1元，所以i<=sum+1
            if(!c1[i]){printf("%d
",i);break;}
    }
    return 0;
}

AC代码二(0ms)：也可以用多重部分和问题解决。最后只要输出使dp[i]<0成立的那个i即为不能凑出第一张面额：i元。

#include<bits/stdc++.h>
using namespace std;
const int a[3]={1,2,5};
int sum,num[3],dp[8005];
int main(){
    while(~scanf("%d%d%d",&num[0],&num[1],&num[2])&&(num[0]+num[1]+num[2])){
        memset(dp,-1,sizeof(dp));dp[0]=0;//前0种数加和为0剩下0的个数为0
        sum=num[0]+num[1]*2+num[2]*5;
        for(int i=0;i<3;++i){
            for(int j=0;j<=sum;++j){
                if(dp[j]>=0)dp[j]=num[i];
                else if(j<a[i]||dp[j-a[i]]<=0)dp[j]=-1;
                else dp[j]=dp[j-a[i]]-1;
            }
        }
        for(int i=1;i<=sum+1;++i)
            if(dp[i]<0){printf("%d
",i);break;}
    }
    return 0;
}

题解报告：Luogu P1164 小A点菜

题目背景

uim神犇拿到了uoi的ra（镭牌）后，立刻拉着基友小A到了一家……餐馆，很低端的那种。

uim指着墙上的价目表（太低级了没有菜单），说：“随便点”。

题目描述

不过uim由于买了一些辅（e）辅（ro）书，口袋里只剩M元(M≤10000)。

餐馆虽低端，但是菜品种类不少，有NN种(N≤100)，第i种卖ai​元(ai​≤1000)。由于是很低端的餐馆，所以每种菜只有一份。

小A奉行“不把钱吃光不罢休”，所以他点单一定刚好吧uim身上所有钱花完。他想知道有多少种点菜方法。

由于小A肚子太饿，所以最多只能等待11秒。

输入输出格式

输入格式：

第一行是两个数字，表示N和M。

第二行起N个正数ai​（可以有相同的数字，每个数字均在1000以内）。

输出格式：

一个正整数，表示点菜方案数，保证答案的范围在int之内。

输入输出样例

输入样例#1：

4 4
1 1 2 2

输出样例#1：

3
解题思路：多重背包计数转化成01背包。
AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,a[105],dp[10005];
int main(){
    while(cin>>n>>m){
        memset(dp,0,sizeof(dp));dp[0]=1;
        for(int i=0;i<n;++i)cin>>a[i];
        for(int i=0;i<n;++i)
            for(int j=m;j>=a[i];--j)//每种只取一个，每次累加都由上一个状态得来
                dp[j]+=dp[j-a[i]];
        cout<<dp[m]<<endl;
    }
    return 0;
}