题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2073
Problem Description
甜甜从小就喜欢画图画,最近他买了一支智能画笔,由于刚刚接触,所以甜甜只会用它来画直线,于是他就在平面直角坐标系中画出如下的图形: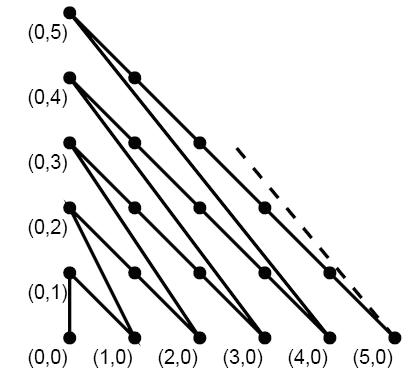

Input
第一个数是正整数N(≤100)。代表数据的组数。 每组数据由四个非负整数组成x1,y1,x2,y2;所有的数都不会大于100。
Output
对于每组数据,输出两点(x1,y1),(x2,y2)之间的折线距离。注意输出结果精确到小数点后3位。
Sample Input
5
0 0 0 1
0 0 1 0
2 3 3 1
99 99 9 9
5 5 5 5
Sample Output
1.000
2.414
10.646
54985.047
0.000
解题思路:这又是一道规律题,每一点都保存前面的值,求两点之间的距离就是各点的和值相减得到的绝对值就行了。仔细观察图片可以得出计算两点之间的距离可以拆分为两部分组成,一个是sqrt(2)的倍数,另一个是sqrt[i*i+(i+1)*(i+1)],其中i是从0~(不包括)x+y(点(x,y)),发现规律后再敲一遍代码,思路清晰。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 double as(int x,int y)//计算(0,0)到(x,y)的折线距离 4 { 5 double t=sqrt(2),ans=0; 6 for(int i=1;i<x+y;i++)//由规律得到先对sqrt(2)进行相乘 7 ans+=t*i; 8 ans+=t*x;//加上此点的横坐标x乘以t即可 9 for(int i=0;i<x+y;i++)//相邻边的平方和 10 ans+=sqrt(i*i+(i+1)*(i+1));//再加上这个规律 11 return ans; 12 } 13 int main() 14 { 15 int N,x1,y1,x2,y2;//两个坐标点 16 cin>>N; 17 while(N--){ 18 cin>>x1>>y1>>x2>>y2; 19 printf("%.3f ",fabs(as(x2,y2)-as(x1,y1)));//相减的绝对值 20 } 21 return 0; 22 }