12770 小L的有向图

题意

 首先，我们定义一个图的价值为其合法拓扑序的个数。

对于一张n个点，m条边的有向图， 它的每一条都可能消失，求其所有形态的价值的和。

(n leq 22, m leq n imes (n-1))
数据保证没有重边，自环(x到y的边和y到x的边不算重边)。

第一个问题：给定一个有向图，求拓扑排序生成的序列数。

首先，我们要明白什么是拓扑序(如果知道什么是拓扑序请略过)

个人理解，拓扑序是拓扑排序后的序列

以下图为例：

​

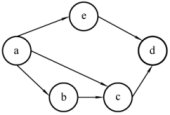
a点没有被其它点指向，d点指向其他任何点，所以拓扑序应该是 a xxx d的格式。

其次，c点要在b点之后，所以上图的拓扑序只有：aebcd、abecd、abced 三个。

接下来是对拓扑序的求解。

可定义状态s的二进制位上的1表示此点已经排好序了。

例如：mask=6时，化为二进制mask=110，表示第2、3个点已经排好序了。

当所有儿子节点排好序的时候，父节点就排好序了。

所以父节点的状态可以由子节点转移而来。

用son[i]表示节点i可以进行转移的合法状态，dp[mask]表示状态为mask的方法数。

for (int mask = 0; mask < all; ++mask) {
  for (int i = 1; i <= n; ++i) {
    if((mask & (1<<i-1) == 0) && (mask & son[i]) == son[i]) {
      dp[mask | (1<<i-1)] += dp[mask];
    }
  }
}

思路

在已知如何求解正常拓扑序个数的基础上，考虑在一个每条边都可能消失的有向图上的所有合法拓扑序的数量。

每个父节点的状态依旧是由子节点转移而来，而由于每条边都可能消失，所以每个子节点对父节点的贡献都是 (dp[mask] * 2) 的。所以，父节点的状态转移方程为：

[dp[mask | (1<<i-1)] = sum {dp[mask] * 2 ^{mask中i的子节点个数}} ]

Code

#include <bits/stdc++.h>

using namespace std;
const int mod = 998244353;
const int maxn = (1<<22)+10;
typedef long long ll;

int n, m, all;
ll dp[maxn] = {1};
int son[24], two[24] = {1}, cnt[maxn];

void add(ll &x, ll y) {
    x += y;
    if(x >= mod) x -= mod;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) two[i] = (two[i-1] << 1) % mod;
    for (int u, v, i = 1; i <= m; ++i) {
        scanf("%d %d", &u, &v);
        son[u] |= (1<<v-1);
    }
    all = 1 << n;
    for (int i = 1; i < all; ++i) cnt[i] = cnt[i>>1] + (i&1);
    for (int mask = 0; mask < all; ++mask) {
        for (int i = 1; i <= n; ++i) {
            if(!(mask & (1<<i-1)))
                add(dp[mask | (1<<i-1)], dp[mask] * two[cnt[son[i] & mask]] % mod);
        }
    }
    printf("%lld
", dp[all-1]);
    return 0;
}