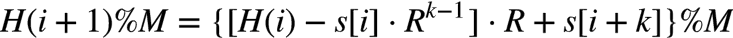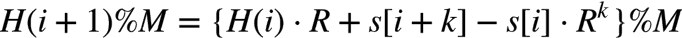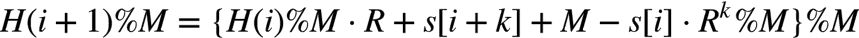Rolling Hash(Rabin-Karp算法)匹配字符串

您可以在我的个人博客中访问此篇文章：

http://acbingo.cn/2015/08/09/Rolling%20Hash(Rabin-Karp%E7%AE%97%E6%B3%95)%E5%8C%B9%E9%85%8D%E5%AD%97%E7%AC%A6%E4%B8%B2/

该算法常用的场景

字符串中查找子串，字符串中查找anagram形式的子串问题。

关于字符串查找与匹配

字符串可以理解为字符数组。而字符可以被转换为整数，他们具体的值依赖于他们的编码方式(ASCII/Unicode)。这意味着我们可以把字符串当成一个整形数组。找到一种方式将一组整形数字转化为一个数字，就能够使得我们借助一个预期的输入值来Hash字符串。
既然字符串被看成是数组而不是单个元素，比较两个字符串是否想到就没有比较两个数值来得简单直接。去检查A和B是否相等，我们不得不通过枚举所有的A和B的元素来确定对于所有的i来讲A[i]=B[i]。这意味着字符串比较的复杂度依赖于字符串的长度。比较两个长度为n的字符串，需要的复杂度为O(n)。另外，去hash一个字符串是通过枚举整个字符串的元素，所以hash一个长度为n的字符串也需要O(n)的时间复杂度。

做法

1. hash P 得到 h(p) 。时间复杂度：O(L)
2. 从S的索引为0开始来枚举S里长度为L的子串，hash子串并计算出h(P)’。时间复杂度为O(nL)。
3. 如果一个子串的hash值与h(P)匹配，将该子串与P进行比较，如果不匹配则停止，如果匹配则继续进行步骤2。时间复杂度：O(L)

这个做法的时间复杂度为O(nL)。我们可以通过使用rollinghash来优化这种做法。在步骤2中，我们看到对于O(n)的子串，都花费了O(L)来hash他们(你可以想象成，找了一个长度为L的框，框住了S，每迭代一次向前移动一位，所以会移动n次，而对于每次每个框中的子串都需要迭代这个子串来算哈希值，所以复杂度为nL)。然而你可以看到这些子串中很多字符都是重复的。比如，看一个字符串“algorithms”中长度为5的子串，最开始的两个子串长度为“algor”和“lgori”。如果我们能利用这两个子串又有共同的子串“lgor”这个事实，将会为我们省去很多时间来处理每一个字符串。看起来我们应该使用rollinghash。

“数值”示例

让我们回到字符串上去，假如我们有P和S都被转化为了两个整形数组：
P=[9,0,2,1,0] (1)
S=[4,8,9,0,2,1,0,7] (2)
长度为5的S的子串被列举在下面：
S0=[4,8,9,0,2] (3)
S1=[8,9,0,2,1] (4)
S2=[9,0,2,1,0] (5)
… (6)
我们想知道P是否能与S的某个子串匹配，可以使用上面的“做法”中的三个步骤。我们的Hash函数可以是：

或者换句话说，我们将长度为5的整形数组中的每个数值都映射到一个5位数的每一位上，然后用这个数值跟m做“mod”运算。h(P)=90210mod m，h(S0)=48902mod m，以及h(S1)=98021mod m。注意这个哈希函数，我们可以是用h(S0)来帮助计算h(S1)。我们从48902开始，去除第一位得到8902，乘以10得到89020，然后加上下一位数值得到：89021.更通用的公式是：

我们可以想象为这是在所有的S的子串上一个滑动的窗口。计算下一个子串的hash值其是值关系到两个元素，这两个元素正好是在这个滑动窗口的两端（一个进来一个出去）。这里与上面有很大的不同，这里我们除了第一次去计算长度为L的第一个子串之后，我们将不在依赖这长度为L的元素集合了，我们只依赖两个元素，这使得计算子串hash值的复杂度变成了O(1)的操作。
在这个数值的示例中，我们看到了简单的按位存放整数，并且设置了“底”为10，因此我们可以很轻易得分离出其中的每个数字。为了通用话，我们可以采用如下通用公式：

并且计算下一个子串的hash值就是：

感觉他解释的不是很清楚。
这里给出个我自己的理解，当n=5,b=10
h(Si+1)=(h(Si)mod(b^n)*b+S[i+L])mod m

而另一位大神是这样描述的:
Rabin-Karp算法的关键思想是 某一子串的hash值可以根据上一子串的hash在常数时间内计算出来，这样比对的时间复杂度可以降为O(n-k)。Rabin-Karp对字符串的hash算法和上面描述的一样（按整数进制解析再求模），假设原字符串为s，H(i)表示第i个字符开始的k个子字符串的hash值，即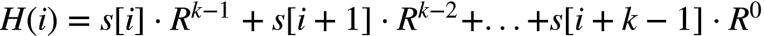
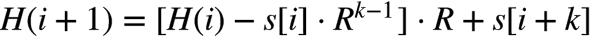
,（先不考虑%M），则，时间为常数。
又由%的性质可得:



即 i+1 处子串的 hash 可以由 i 处子串的 hash 直接计算而得，在中间结果 %M 主要是为了防止溢出。
M 一般选取一个非常大的数字，子串的数目相对而言非常少，产生散列碰撞的概率为 1/M，可以忽略不计。
代码实现如下，这里当hash一致时没有再回退检查。可以看到 Rabin-Karp 的瓶颈在于每个内循环都进行了乘和模运算，模运算是比较耗时的，而其他算法大部分只需要进行字符比对.

回到字符串的问题上

既然字符串可以被转换为数字，我们可以在字符串上也像跟数值的示例一样用同样的方法来提高运行效率。算法实现如下：

1. Hash P 得到h(P) 时间复杂度为O(L)
2. Hash S中长度为L的第一个子串 时间复杂度为O(L)
3. 使用rolling hash 方法来计算S 所有的子串 O(n)，并以计算出的hash值与h(P)进行比较 时间复杂度为O(n)
4. 如果一个子串的hash值与h(p)相等，那么将该子串与P进行比较，如果匹配则继续，否则则中断当前匹配 时间复杂度为O(L)

这加快了整个算法的效率，只要所有做比较的总时间为O(n)，那么整个算法的时间复杂度为O(n)。我们进入一个问题，如果我们在我们的hashtable中假设产生了O(n)次“哈希碰撞”（指由于哈希函数的问题，导致多个key对应到同一个值），那么步骤4的总复杂度就为O(nL)。因此我们不得不确保我们的hashtable的大小为n（也就是必须保证每个子串都能唯一对应一个哈希key，这取决于hash函数的设计），这样我们就可以期待子串可以被一次命中，所以我们只需要走步骤4O(1)次。而我们步骤4的时间复杂度为O(L)，在这种情况下，我们仍然可以保证整个问题的时间复杂度为O(n)

代码实现

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

#include <iostream> #include <string> using namespace std; void Rabin_Karp(string p,string s,int b,int m){ int hash_p=0;//目标串的hash值 int hash_i=0;//当前串的hash值 int h=1; for (int i=0;i<p.size();i++){//h==pow(b,p.size()); h=(h*b)%m; } for (int i=0;i<p.size();i++){ hash_p=(b*hash_p+p[i])%m; hash_i=(b*hash_i+s[i])%m; } for (int i=0;i<=s.size()-p.size();i++){ if (hash_i==hash_p){ int j; for (j=0;j<p.size();j++){ if (s[i+j]!=p[j]) break; } if (j==p.size()) cout<<"yes "<<i<<endl; } if (i<s.size()-p.size()){ hash_i=(hash_i%m*b+s[i+p.size()]+m-s[i]*h%m)%m;//算出下一个hash值 if (hash_i<0) hash_i=hash_i+m;//其实这一步在该程序下是没有实际意义的。主要是提醒自己以后涉及到取余问题的时候可能会发生取到负数及0 } } } int main () { string p,s; p="Rabin"; s="Rabin–Karp string search algorithm: Rabin-Karp"; int m=101;//素数 int base=26;//基数,这里取26好了 Rabin_Karp(p,s,base,m); return 0; }

自身匹配问题

给定一个长度为n的串s，求其子串中是否存在相同的且长度都为l的串，若存在，输出其出现次数以及出现位置。
注意此处要求子串长度是一定的，数据小的话暴力就可以搞。

1. hash S的第一个长度为L的子串 时间复杂度为：O(L),放入map表
2. 使用rolling hash 来计算S的所有O(n)个子串,每算出一个然后和map表进行比对，并更新map表，时间为O(nlogn)
   注意可能会发生“哈希碰撞”。总的来说，m值的大小决定了map表的大小，而map表的大小又决定了哈希碰撞的概率。若是发生了碰撞，个人认为采用缓存区法或者再哈希都比较容易实现。

代码实现

代码只实现了判断是否存在相同的子串，╮(╯-╰)╭，没办法，lpl马上开赛了，得赶紧干完呢~

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45

#include <iostream> #include <string> #include <map> using namespace std; struct Node{ int index; int num; }; map<int,Node> mymap; void Rabin_Karp_Self(string s,int l,int b,int m) { int h=0;//注意初始化 int t=1; for (int i=0;i<l;i++) t=(t*b)%m; for (int i=0;i<l;i++){//计算第一个窗口的hash值 h=((b*h)+s[i])%m; } mymap[h].index=0;mymap[h].num++; for (int i=1;i<=s.size()-l;i++){ //算初当前的hash h=(h%m*b+s[i-1+l]+m-s[i-1]*t%m)%m;//滑动窗口，计算下一个hash值 //h=((h*b-s[i-1]*t)+s[i+l-1])%m; //if (h<0) h+=m; //这里同上题 if (mymap.count(h)){ int j; for (j=0;j<l;j++) { if (s[j+mymap[h].index]!=s[i+j]) break; } if (j==l) cout<<"yes "<<mymap[h].index<<" "<<i<<endl; }else { mymap[h].index=i;mymap[h].index++; } } } int main () { string s; int n; s="Rabin–Karp string search algorithm: Rabin-Karp"; //s="abcabc"; n=5; int b;int m; b=10;m=10001; Rabin_Karp_Self(s,n,b,m); return 0; }

若想输出次数和位置，也很简单，node增加一个数组，然后修改下cout那就行了。另外注意哈希碰撞的处理。

不定长的子串

TODO
等对字符串匹配问题的各种算法理解都十分透彻后，再回头考虑这个问题
个人认为求不定长子串匹配问题该算法不仅麻烦，时间也算不上最快的。

共同子串问题

刚才的算法被设计成：在一个字符串S中查找一个模式串P的匹配。然而，现在我们需要处理另一个问题：看看两个长度为n的长字符串S和T，看他们是否拥有长度为L的共同子串。这看起来是一个更难处理的问题，但我们还是能有采用rollinghash使得其复杂度为O(n)。我们采用一个相似的策略：

1. hash S的第一个长度为L的子串 时间复杂度为：O(L)
2. 使用rolling hash 来计算S的所有O(n)个子串，然后把每个子串加入一个hash table中 时间复杂度为：O(n)
3. hash T的第一个长度为L的子串 时间复杂度为：O(L)
4. 使用rolling hash方法来计算T的所有O(n)个子串，对每个子串，检查hashtable看是否能命中。
5. 如果T的一个子串命中了S的一个子串，那么就进行匹配，如果相等则继续，否则停止匹配。时间复杂度为：O(L)

然而，保持运行的次数为O(n)，我们又再次需要注意限制“哈希碰撞”的次数，以减少我们进入步骤5来进行不必要的匹配。这次，如果我们的hashtable的大小为O(n)，那么我们对于T的每个子串所期待的命中复杂度为O(1)(最坏的情况)。这样的结果会导致字符串进行O(n)次比较，总共的复杂度为O(nL)次，这使得字符串的比较在这里成为了瓶颈。我们可以扩大hashtable的大小，同时修改我们的hash函数使得我们的hashtable有O(n的平方)个槽（槽指hash表中真正用于存储数据的单元），来使得对于每个T的子串来讲，可能的碰撞降低到O(1/n)。这可以解决我们的问题，并且使得整个问题的复杂度仍然为O(n)，但我们可能没有必要像这样来创建这么大的hashtable消耗不必要的资源。
取而代之的是，我们将利用字符串签名的优势来替代消耗更多存储资源的做法，我们将再为每个子串分配一个hash值，称之为h(k)’。注意，这个h(k)’的hash 函数最终将字符串映射到0到n的平方的范围而不是上面的0到n。现在当我们在hashtable中产生哈希碰撞时，在我们做最终“昂贵”的字符串比较之前，我们首先可以比较两个字符串的签名，如果签名不匹配，那么我们就可以跳过字符串比较。对于两个子串k1和k2，仅当h(k1)=h(k2)以及h(k1)’=h(k2)’时，我们才会做最终的字符串比较。对于一个好的h(k)’的哈希函数，这将大大减少字符串比对，使得比对的复杂度接近O(n)，将共同子串问题的复杂度限制在O(n)。

二维扩展

http://novoland.github.io/%E7%AE%97%E6%B3%95/2014/07/26/Hash%20&%20Rabin-Karp%E5%AD%97%E7%AC%A6%E4%B8%B2%E6%9F%A5%E6%89%BE%E7%AE%97%E6%B3%95.html
参考自:
http://blog.csdn.net/yanghua_kobe/article/details/8914970
http://novoland.github.io/%E7%AE%97%E6%B3%95/2014/07/26/Hash%20&%20Rabin-Karp%E5%AD%97%E7%AC%A6%E4%B8%B2%E6%9F%A5%E6%89%BE%E7%AE%97%E6%B3%95.html
http://blog.csdn.net/chenhanzhun/article/details/39895077