态规划算法是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推的方式去解决。
动态规划的核心点:定义状态与转移方程(最优子结构)
重新定义问题:

一、最长上升子序列(LIS):给定一个序列X,求X长度最大的连续递增的子序列。
例:X=[1,7,2,8,3,5,2],LIS(X)=[1,2,3,5]

def LIS(x): F = [0 for _ in range(len(x))] p = [-1 for _ in range(len(x))] # 初始化 F[0] = 1 p[0] = -1 for k in range(1, len(F)): max_loc = -1 max_num = 0 # 内层循环表示F[0:k]里所有小于x[k]的对应位置的F[i]的最大值 for i in range(0, k): if x[i] < x[k]: if F[i] > max_num: max_loc = i max_num = F[i] F[k] = max_num + 1 p[k] = max_loc max_i = 0 for i in range(1,len(F)): if F[i] > F[max_i]: max_i = i lis = [] i = max_i while i >= 0: lis.append(x[i]) i = p[i] lis.reverse() return lis # print(LIS([9,7,2,8,3,5,2]))
二、最长公共子序列(LCS)问题:给定两个序列X和Y,求X和Y长度最大的公共子序列。
例:X="ABBCBDE" Y="DBBCDB" LCS(X,Y)="BBCD"
动态规划最优子结构:

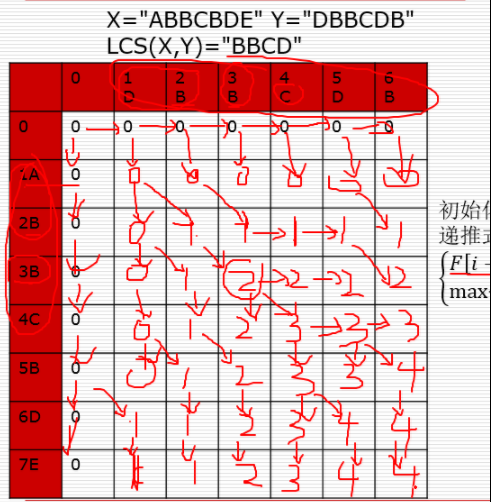
def LCS(x, y): F = [[0 for _ in range(len(y)+1)] for _ in range(len(x)+1)] p = [[0 for _ in range(len(y)+1)] for _ in range(len(x)+1)] for i in range(1, len(x)+1): p[i][0] = 2 for j in range(1, len(y)+1): p[0][j] = 1 # 0 斜向 1 横向 j-1 2竖向 i-1 for i in range(1, len(x)+1): for j in range(1, len(y)+1): if x[i-1] == y[j-1]: F[i][j] = F[i-1][j-1]+1 p[i][j] = 0 else: #F[i][j] = max(F[i-1][j], F[i][j-1]) if F[i-1][j] > F[i][j-1]: F[i][j] = F[i-1][j] p[i][j] = 2 else: F[i][j] = F[i][j-1] p[i][j] = 1 lcs = [] i = len(x) j = len(y) while i > 0 or j > 0: if p[i][j] == 0: lcs.append(x[i-1]) i -= 1 j -= 1 elif p[i][j] == 1: j -= 1 else: i -= 1 lcs.reverse() return lcs #return F[i][j] # print(LCS("ABBCBDE", "DBBCDB"))
三、最长公共子序列(LCSS)问题:给定两个序列X和Y,求X和Y长度最大的公共子串。
例:X="ABBCBDE" Y="DBBCDB" LCSS(X,Y)="BBC"
暴力搜索求解:O(n3)
动态规划最优子结构:

def LCSS(x, y): F = [[0 for _ in range(len(y)+1)] for _ in range(len(x)+1)] p = [[0 for _ in range(len(y)+1)] for _ in range(len(x)+1)] # 0 不匹配 1匹配 for i in range(1, len(x)+1): for j in range(1, len(y)+1): if x[i-1] == y[j-1]: F[i][j] = F[i-1][j-1]+1 p[i][j] = 1 else: F[i][j] = 0 p[i][j] = 0 max_val = 0 max_i = 0 max_j = 0 for i in range(1, len(x)+1): for j in range(1, len(y)+1): if F[i][j] > max_val: max_val = F[i][j] max_i = i max_j = j #tracback lcss = [] i = max_i j = max_j while p[i][j] == 1: lcss.append(x[i-1]) i -= 1 j -= 1 lcss.reverse() return lcss print(LCSS("ABBCBDE", "DBBCDB"))
四、编辑距离:指两个字串之间,由一个转成另一个所需的最少编辑操作次数。
允许的编辑操作:替换、插入、删除x="cofe" y="coffee",编辑距离为2(插入2次)
- x="coffee" y="coffe",编辑距离为(删除1次)
- x="coffee" y="coffye",编辑距离为(替换2次)
- x="cofye" y="coffee",编辑距离为2
编辑距离可以用来表示两个字符串的相似度,应用广泛
动态规划最优子结构:

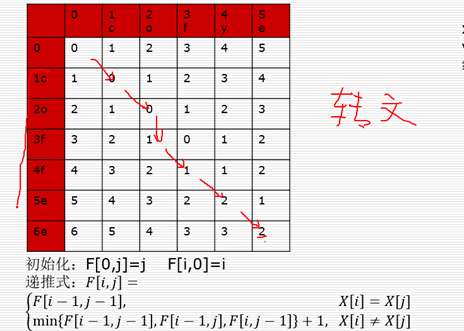
斜着过来是替换
从左边来的是插入
从上面来的是删除

代码待续。。。。。。。。。。