62. Search in Rotated Sorted Array【medium】

62. Search in Rotated Sorted Array【medium】

Suppose a sorted array is rotated at some pivot unknown to you beforehand.

(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

Have you met this question in a real interview? 

Yes

Example

For [4, 5, 1, 2, 3] and target=1, return 2.

For [4, 5, 1, 2, 3] and target=0, return -1.

Challenge 

O(logN) time

错误解法：

class Solution {
public:
    /*
     * @param A: an integer rotated sorted array
     * @param target: an integer to be searched
     * @return: an integer
     */
    int search(vector<int> A, int target) {
        if (A.size() == 0) {
            return -1;
        }
        
        int start = 0;
        int end = A.size() - 1;
        
        while (start + 1 < end) {
            int mid = start + (end - start) / 2;
            
            if (A[mid] == target) {
                return mid;
            }
            else if (A[mid] < target) {
                // 5 6 1 2 3 4
                if (A[mid] > A[start]) {
                    start = mid;
                }
                // 5 6 1 2 3 4
                else { // mid < target && mid <= start
                    end = mid;
                }
            }
            else if (A[mid] > target) {
                
                if (A[mid] < A[end]) { // mid > target && mid < end
                    end = mid;
                }
                // 3 4 5 6 1 2 找3
                else { // mid > target && mid >= end
                    start = mid;
                }
            }
        }

        if (A[start] == target) {
            return start;
        }

        if (A[end] == target) {
            return end;
        }

        return -1;
    }
};

一开始思考的方向就不对，搞晕了……

解法一：

class Solution {
public:
    /*
     * @param A: an integer rotated sorted array
     * @param target: an integer to be searched
     * @return: an integer
     */
    int search(vector<int> A, int target) {
        if (A.size() == 0) {
            return -1;
        }
        
        int start = 0;
        int end = A.size() - 1;
        
        while (start + 1 < end) {
            int mid = start + (end - start) / 2;
            
            if (A[mid] == target) {
                return mid;
            }
            
            if (A[mid] >= A[start]) {
                if (A[start] <= target && target <= A[mid]) {
                    end = mid;
                }
                else {
                    start = mid;
                }
            }
            else {
                if (A[mid] <= target && target <= A[end]) {
                    start = mid;
                }
                else {
                    end = mid;
                }
            }
        }

        if (A[start] == target) {
            return start;
        }

        if (A[end] == target) {
            return end;
        }

        return -1;
    }
};

借鉴网上的一个图，可以清楚的归纳一下思路，那么代码就好写了。

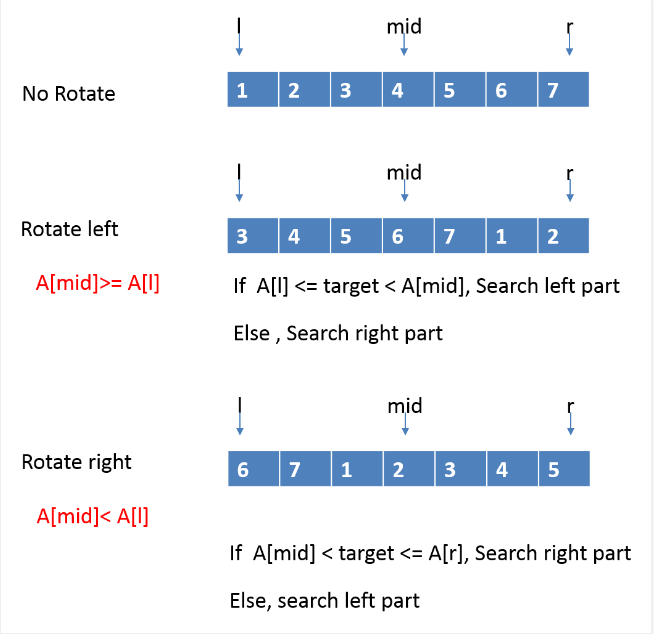
这个图参考了：http://fisherlei.blogspot.com/2013/01/leetcode-search-in-rotated-sorted-array.html

解法二：

class Solution {
public:
    int search(int A[], int n, int target) {
        return searchRotatedSortedArray(A, 0, n-1, target);
    }
    
    int searchRotatedSortedArray(int A[], int start, int end, int target) {
        if(start>end) return -1;
        int mid = start + (end-start)/2;
        if(A[mid]==target) return mid;
        
        if(A[mid]<A[end]) { // right half sorted
            if(target>A[mid] && target<=A[end])
                return searchRotatedSortedArray(A, mid+1, end, target);
            else
                return searchRotatedSortedArray(A, start, mid-1, target);
        }
        else {  // left half sorted
            if(target>=A[start] && target<A[mid]) 
                return searchRotatedSortedArray(A, start, mid-1, target);
            else
                return searchRotatedSortedArray(A, mid+1, end, target);
        }
    }
};

解法三：

class Solution {
public:
    int search(int A[], int n, int target) {
        int start = 0, end = n-1;
        while(start<=end) {
            int mid = start + (end-start)/2;
            if(A[mid]==target) return mid;  
            
            if(A[mid]<A[end]) { // right half sorted
                if(target>A[mid] && target<=A[end])
                    start = mid+1;
                else
                    end = mid-1;
            }
            else {  // left half sorted
                if(target>=A[start] && target<A[mid]) 
                    end = mid-1;
                else
                    start = mid+1;
            }
        }
        return -1;
    }
};

解法二和解法三参考了：http://bangbingsyb.blogspot.com/2014/11/leetcode-search-in-rotated-sorted-array.html

思路如下：

题目一看就知道是binary search。所以关键点在于每次要能判断出target位于左半还是右半序列。解这题得先在纸上写几个rotated sorted array的例子出来找下规律。Rotated sorted array根据旋转得多少有两种情况：

原数组：0 1 2 4 5 6 7
情况1：  6 7 0 1 2 4 5    起始元素0在中间元素的左边
情况2：  2 4 5 6 7 0 1    起始元素0在中间元素的右边

两种情况都有半边是完全sorted的。根据这半边，当target != A[mid]时，可以分情况判断：

当A[mid] < A[end] < A[start]：情况1，右半序列A[mid+1 : end] sorted
A[mid] < target <= A[end], 右半序列，否则为左半序列。

当A[mid] > A[start] > A[end]：情况2，左半序列A[start : mid-1] sorted
A[start] <= target < A[mid], 左半序列，否则为右半序列

最后总结出：
A[mid] =  target, 返回mid，否则

(1) A[mid] < A[end]: A[mid+1 : end] sorted
A[mid] < target <= A[end]  右半，否则左半。

(2) A[mid] > A[end] : A[start : mid-1] sorted
A[start] <= target < A[mid] 左半，否则右半。